Del2: Simulating log-depth threshold circuits for multiplication

1 Program description

This program simulates threshold circuits for multiplication on two 5-bit numbers. Given two numbers in 5-bit binary form, the program constructs a circuit consisting of only threshold gates. This circuit calculates the multiple of these two numbers. It has depth of O(log n), and size of O(n), where n is the number of bits for each input.

2 Background

We will use the following problem definition.

• Problem: ADD
  

  Input: two n bit numbers a = a_n-1 ...a₀ and b = b_n-1... b₀

  Output: s = s_n...s₀, s =_def a + b

• Problem: ITADD
  

  Input: n numbers in binary with n bits each

  Output: the sum of the input numbers in binary

• Problem: LOGITADD
  

  Input: log n numbers with n bits each

  Output: the sum of the input numbers in binary

• Problem: BCOUNT
  

  Input: n bits a_n-1,...,a₀

  Output: the sum of a_i, where i from 0 to n

• Problem: MULT
  

  Input: two n bit numbers

  Output: the product of the input numbers in binary

• Problem: Tⁿ_m
  

  Input: two n bits numbers a_n-1,..., a₀, w_n-1,..., w₀, and
    a threshold m (m is an integer and 0<m<n)

  Output:

  1 if an-1*wn-1 +...+a0*w0 >= m;

  0 otherwise

3 Algorithm

Given two n bit numbers a = a_n-1 ...a₀ and b = b_n-1 ...b₀, first, we can reduce MULT to ITADD by using the school method for multiplication.

Define

• c_i = 0^n-i-1a_n-1... a₁a₀0ⁱ, if b_i = 1; 0^2n-1otherwise.

Then the product of a, b is the sum of c_i, where 0<=i<n. Now our problem turns out to solve ITADD.

Given the above c_i we define for every position k, 0<=k<2n-1, the sum s_k = Σ _i=0^n-1c_i,k. Every s_k can be written in binary using no more than log(n) bits, so we have

Σ_i=0^n-1c_i,k = Σ_j=0^log(n)-1s_k,j * 2^j

Therefore,

Σ_i=0^n-1 c_i= Σ_j=0^n-1 Σ_j=0^n-1 s_k,j*2^j

= Σ _j=0^log(n)-1 Σ_j=0^n-1 s_k,j*2^j*2^k.

Notice that the problem of counting each s_k is a BCOUNT problem. Thus we can reduce the problem of adding n numbers to that of adding log(n) numbers Σ_k=0^n-1s_k,j *2^j+k, where 0<=k<log(n). Each of these numbers has no more than n+log(n) bits. We can iterate this procedure, that is, continue to add the above log(n) numbers using the same method, next time we get log(log(n)) numbers with n+log(n )+log(log(n)) bits, and so on. After x iterations, where x is the smallest number such that log^x+1n<=2, we have 2 numbers at the end, we can add them using a constant depth circuit described in [Vol00].

Next, we reduce BCOUNT to Tⁿ_m. Let l = log(n), Σ_i=0^n-1s_i = s_l-1 ... s₀ in binary. Let 0<=j<log(n). Let R_j be the set of those numbers r ∈{0, ..., n} whose j-th bit is on (where the 0^th bit is the rightmost bit, and the (l-1)th bit is the leftmost bit). We have,

S_j = ∪_{r ∈Rj} (Σ_i=0^n-1s_i = r).

Obviously,

(x = r) = (x >= r) AND NOT( x >= r+1)

thus,

S_j = ∪_{r ∈ Rj} (Tⁿ_r (a_1, ..., a_n) Tⁿ_r+1 (a_1, ..., a_n)).

Observe that the set R_j do not depend on the input value but only on the input length n and thus can be hardwired into the circuit. Now we have a circuit for BCOUNT which uses (Tⁿ_r) _{n ∈ N} and (Tⁿ_r+1) _{n ∈N} gates.

To construct a multiplication circuit we also need to use the NOT, AND, OR gates. It is easy to see that:

AND = Tⁿ_n (w_i = 1, where 0<=i<n)

OR = Tⁿ₁ (w_i= 1, where 0<=i<n)

NOT = T¹₀ (w = -1)

Based on the above reductions, we can construct a circuit for MULT with only threshold gates.

4 Design and Implementation

Overall circuit design

Given two 5-bit numbers, to calculate the product, our program first generates a circuit, the inputs for this circuit are two 5-bit numbers. The evaluation is the process of calculation, and the evaluation result is the multiple of two numbers. The program generates the circuit only once, after each evaluation (calculation), it can reset the circuit for next evaluation. Figure 1 shows this multiplication circuit.

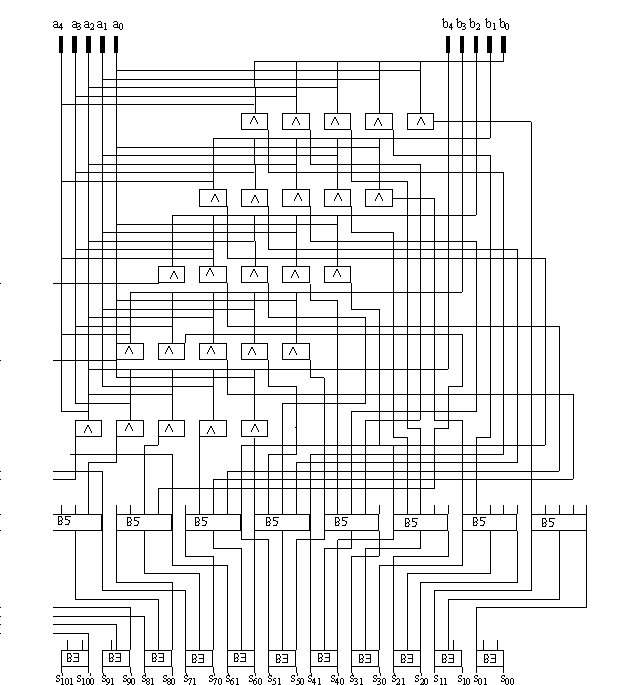
Figure 1. Circuit for calculating the product of two five bits binary numbers

The depth of the circuit is seven. In first five levels we prepare c_i,k (where 0<=i<n, 0<=k<2n-1), then we send c_i,k to the sixth level, that is, five numbers with nine bits each need to be added. Level six contains nine BCOUNT gates, where each gate has five input and three output bits. After applying level six, we have three numbers with nine bits each. We now send them to the seventh layer, which consists of 11 BCOUNT gates with three inputs and two outputs each. After this level, we get two 13-bit numbers. Adding two binary numbers can be done by a constant depth circuit that is described in [Vol00].

In Figure 1, the constructed circuit for MULT is made up of BCOUNT gates with five or three input bits. Each BCOUNT gate can be construct by a constant depth circuit including threshold, AND, OR, and NOT gates. Figure 2 illustrates the construction of a five inputs and three outputs BCOUNT gate using threshold, AND, OR gated. Figure 3 illustrates the construction of a three inputs and two outputs BCOUNT gate using threshold, AND, OR gated. We can further replace each AND, OR, NOT gate with threshold gates as described in section 3.

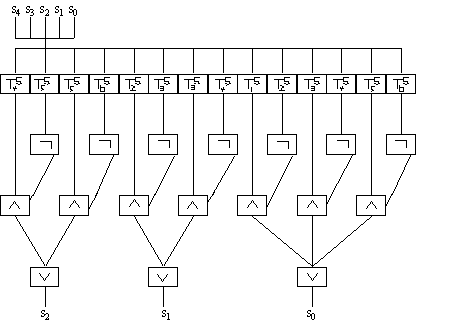
Figure 2 BCOUNT circuit with five inputs and three outputs

 

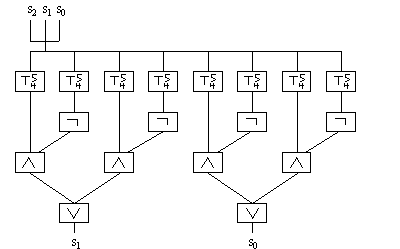Figure 3 BCOUNT circuit with three inputs and two outputs

Given two n bit numbers, according to our circuit construction, we need log^*(n) layers of BCOUNT gates. Each layer can be implemented by a constant depth threshold circuit. Thus the total depth of the threshold circuit for multiplication is O(log^*(n)).

Program organization

Basically, three structures are designed: pin, threshold and blkbox structure.

• In pin structure, we record input and output information using link-lists respectively. Each element of a link-list is a pointer that points to a pin.
• A threshold gate has input and output pins, and its k of threshold value.
• A blkbox is a structure made of input pins, output pins, and internal threshold gates. We can set different blkbox structures to implement AND, OR, NOT, or BCOUNT gates.

Having all these elements, we can finally construct our circuit for multiplication. Figure 4 shows our program organization

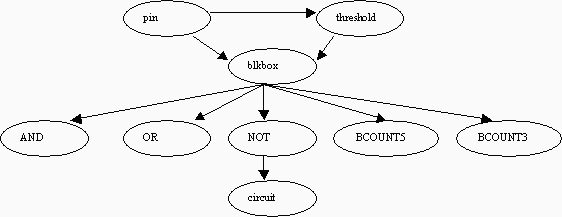
Figure 4 Program organization diagram

5 Test result

A test program is written, which takes the circuit as its input and evaluate step-by-step the status and value of the threshold gates. Because this circuit is only calculating the multiple of two 5-bit binary numbers, it is possible to verify each possible input and the evaluation result. My evaluations show that my circuit correctly computed the product of two 5-bit numbers in constant time.

6 References:

[Vol00] Introduction to Circuit Complexity. H.Vollmer. Springer-Verlag. 1999.

7 Code