Deliverable 4

Description: Implement a homomorphic encryption by reading relevant papers and coding a working encryption mechanism. The methodology chosen is Pailler encryption, which is a partial homomorphic encryption scheme

Implementation steps:

• Generate a public-private key pair
• Encrypt a number
• Decrypt a number

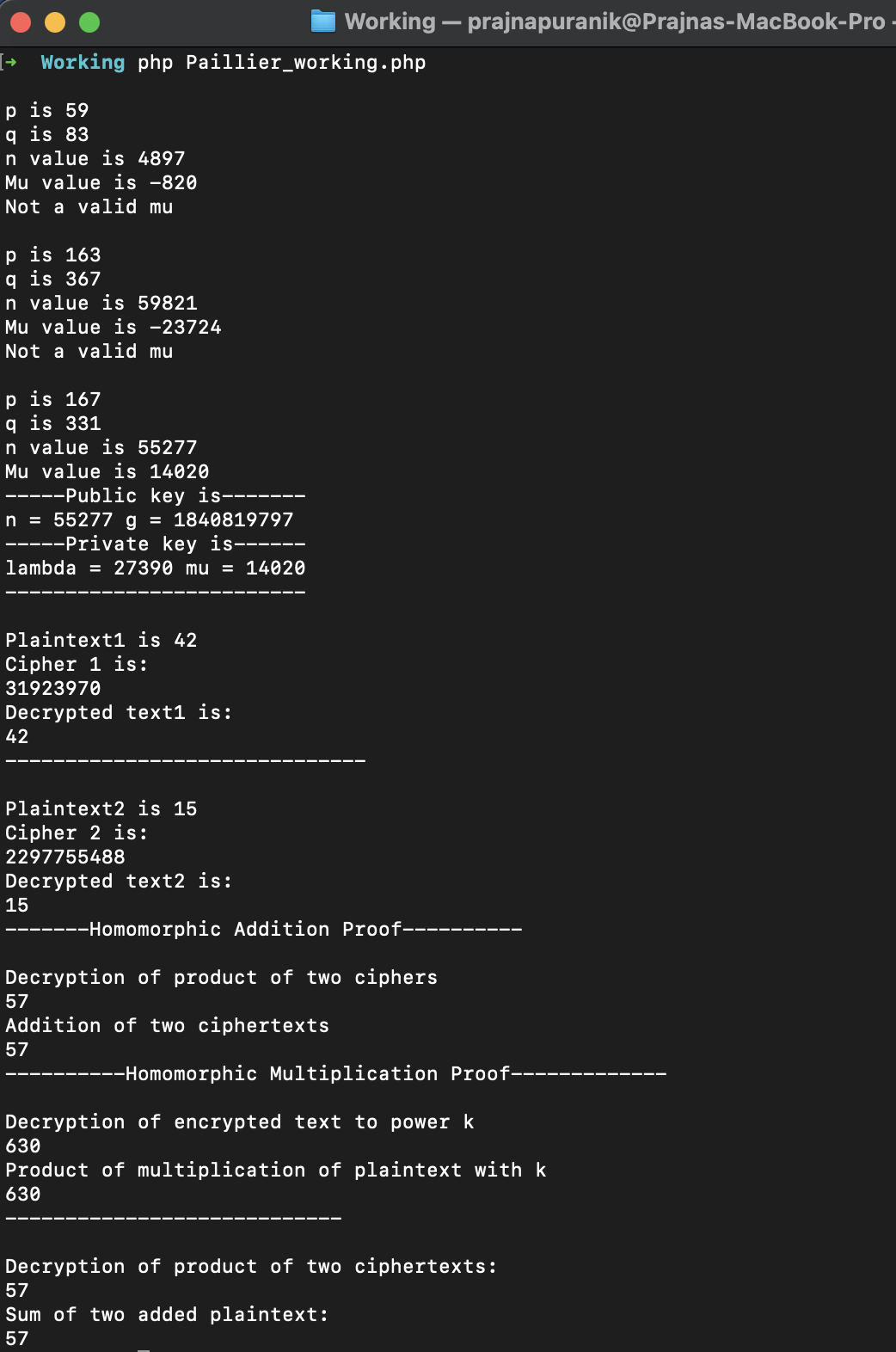
Working of key generation function:

• Pick two large prime numbers p and q randomly and independently
• Confirm that gcd of pq and product of 1-p and 1-q is 1. This property is assured if both primes are of equal length
• Compute n is product of p and q and the lambda is the lcm of p-1 and q-1
• Pick a random integer g in the set of integers from 1 to n2
• Define function L which is division of x-1 by n
• Calculate multiplicative modulo inverse mu. If it doesn't exist, choose new p and q and repeat
• The public key is n and g
• The private key is lambda and mu
• Prove the homomorphic properties of paillier encryption scheme

Working of encryption function:

• Encryption can work for any m in the range 0 to n
• Select random number r such that r value is between 0 and n
• Compute ciphertext as pow(g, m) * pow(r, n) * mod n^2

Working of decryption function:

Decrypt ciphertext using L(pow(c, lambda) * mod n^2) * mu * mod n

Results