Deliverable 4
Description: Implement a homomorphic encryption by reading relevant papers and coding a working encryption mechanism. The methodology chosen is Pailler encryption, which is a partial homomorphic encryption scheme
Implementation steps:
- Generate a public-private key pair
- Encrypt a number
- Decrypt a number
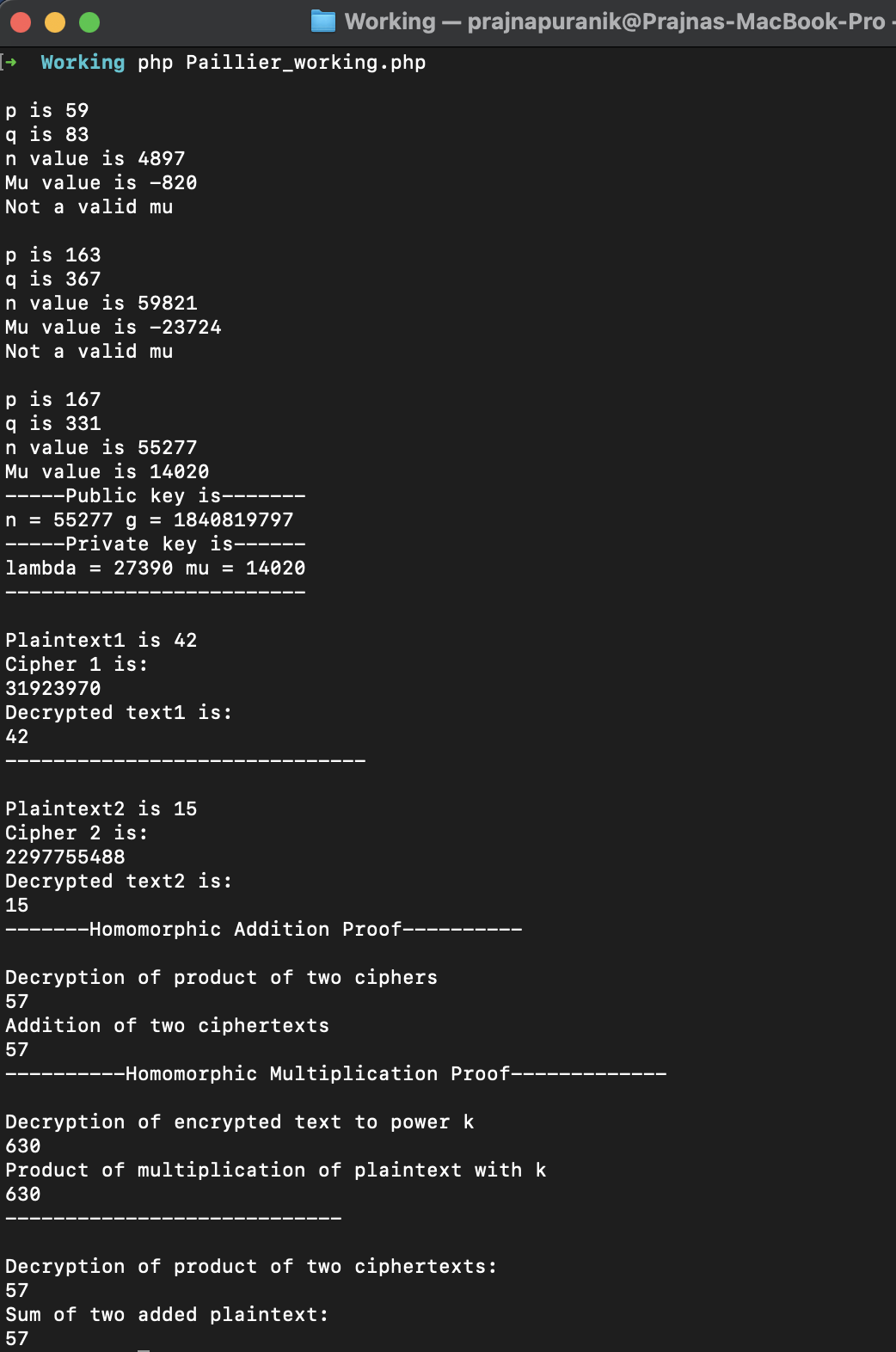
Working of key generation function:
- Pick two large prime numbers p and q randomly and independently
- Confirm that gcd of pq and product of 1-p and 1-q is 1. This property is assured if both primes are of equal length
- Compute n is product of p and q and the lambda is the lcm of p-1 and q-1
- Pick a random integer g in the set of integers from 1 to n2
- Define function L which is division of x-1 by n
- Calculate multiplicative modulo inverse mu. If it doesn't exist, choose new p and q and repeat
- The public key is n and g
- The private key is lambda and mu
- Prove the homomorphic properties of paillier encryption scheme
Working of encryption function:
- Encryption can work for any m in the range 0 to n
- Select random number r such that r value is between 0 and n
- Compute ciphertext as pow(g, m) * pow(r, n) * mod n^2
Working of decryption function:
Decrypt ciphertext using L(pow(c, lambda) * mod n^2) * mu * mod n
Results