Chris Pollett > Students > Yunxuan
Print View
[Bio]
[Blog]
[Final Step of Shor's and Grover's Algorithms]
[Threshold of Error Correction]
[Random-kSAT-Generator: Version 1]
[Random-kQSAT-Generator: Version 2]
[Random-kQSAT-Generator: Version 3]
[Antiferromagnetic Heisenberg Model]
[Random-kQSAT-Generator: Version 4]
[Random-kQSAT-Generator: Version 5]
[Random-kQSAT-Generator: Version 6]
[Thesis]
Here is my data for 2SAT, 3SAT, 4SAT and 5SAT with 7 variables and data range(1-15 clauses). I also tried 14 variables, but the computer freezes for the entire data range (1-20 clauses). So I guess 7 variable is the best choice for getting interesting data. I am slightly mystified by the result. I tried to find what is wrong with my code but I haven't found any mistakes such as index mistakes.
Here is my chief criteria for looking at my data:
when ever there is a cycle, the problem is unsolvable. Meaning...
- To get an unsatisfiable in the 2SAT case it take at least 4 clauses.
- To get an unsatisfiable in the 3SAT case it take at least 8 clauses.
- To get an unsatisfiable in the 4SAT case, it takes at least 16 clauses.
- To get an unsatisfiable in the 5SAT case, it takes at least 32 clauses.
As you can see in my data, it is easier to satisfy k-SAT when k is higher, which is what I expected.
Other than my chief criteria, there are some other reasons for problem to be unsatisfiable:
- A variable is fixed then later contradicted later based on another part of the problem.
- Variables can repeat. But this actually cause problems to be less constrained so there should be more solutions, not less.
Why this Lab is a little futile for judging my skill:
- The logic of the solver could be wrong even and still will not affect the solution. It can be wrong because the program spits out false solutions, even the number of solutions could be wrong, and still not affect the result. My point is, the program could be written wrong without changing what result I get.
Conclusion: One point in the debate of whether quantum computer is as powerful as classical computer is the clause to variable ratio of a barely solvable problem. Currently it is higher for classical computers(4.267) than for quantum computers (3.594). Personally, I am not that worried about my clause to variable ratio and what I am suppose to get based on the articles that Prof. Pollett gave me. In those articles the ratio they gave are for the "best" algorithm. While the value I get in my algorithm, is just based off a random algorithm produced by my imagination. But this lab does leave an open ended question: How do I make a program that will give a higher clause to variable ratio?
I finally realize what is wrong with my code! I am going to fix the mistakes, and make new tables and graphs.
Second Week: Hi! I fixed the mistakes in my code. They were: I did not renew chain and stack, also I did not take care of logic contradiction within the clause. But now the problems are fixed. The data is more believable. Last week I was very puzzled by the fact that when I just have one clause, the problem still does not satisfy, how was that possible!! The error that caused this was that I did not renew stack for every time the loop runs. Now it has been verified by me that larger clause size is easier to satisfy and smaller number of clauses are easier to satisfy. This seems correct based on intuition. But tell me if I am wrong.
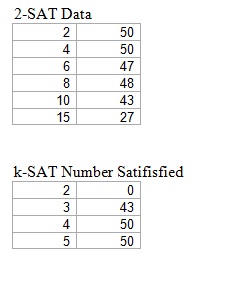
My data range for last week was (1-15 clauses), but I found that for 3-SAT, 4-SAT, and 5-SAT, there are mostly 100% satisfaction guaranteed. I just told you about the k=3,4,5 cases; now I will just put up the 2-SAT data since it is actually not 50 out of 50 unlike the other k values.
Also, since the classical ration was about 4, so I did a 28-clause (7*4=28) run through for k=2,3,4,5 cases, and I put the data table below.