Chris Pollett > Students > Yunxuan
Print View
[Bio]
[Blog]
[Final Step of Shor's and Grover's Algorithms]
[Threshold of Error Correction]
[Random-kSAT-Generator: Version 1]
[Random-kQSAT-Generator: Version 2]
[Random-kQSAT-Generator: Version 3]
[Antiferromagnetic Heisenberg Model]
[Random-kQSAT-Generator: Version 4]
[Random-kQSAT-Generator: Version 5]
[Random-kQSAT-Generator: Version 6]
[Thesis]
jQuantum is a program that allows us to simulate a quantum computer on a classical computer. You can design quantum circuits with it and let them run. The current state of the quantum register is illustrated. It was designed for people who want to write quantum algorithms. This program is currently open source, with its entire code published on-line so that other people can check the correctness of the implemented quantum gates, and suggest new quantum gates or algorithms to be added. The program requires Java 5 or higher to run.
Fast Fourier Transform:

Register: FFT
- In FFT, our aim is to convert a time-domain function into a frequency domain function.
- The FFT is a divide and conquer algorithm that divides the transform into two pieces of size N/2 each step all the way down to single elements, this is the first step and it is also called the time domain decomposition, and it is done by the bit reversal sorting section of the code, which is the first for-loop you see.
- By the way, you have to make sure the array size for your input is 2^(# of bits), or else you will get array index out of bound error.
- FFT time domain decomposition happens to be implemented by sorting the samples according to bit reversed order.
- What the bit reversal does is, for example inputing: 000, 001, 010, 011, 100, 101, 110, and 111, gives the output as: 000, 100, 010, 110, 001, 101, 011, and 111.
- The second step is FFT synthesis. In FFT synthesis, we multiply the odd-half frequency spectrum by a sinusoid and add or subtract it from the even-half frequency spectrum.
- Then putting the result into an array, gives us the entire frequency spectrum. All this is accomplished by the second for-loop.
Quantum Fourier Transform:
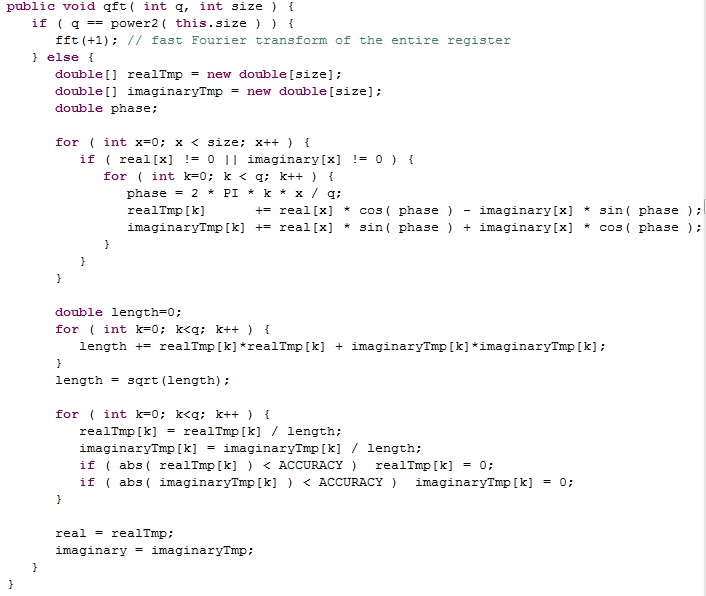
Register: QFT
- Do not be fooled by the length of this code. The QFT section is conceptually much easier than the FFT section above.
- In the Quantum Fourier Transform, the first step is to use the FFT algorithm to get the frequency spectrum of the quantum state function.
- The second step is to multiply each term of the spectrum by the necessary factors (the amplitude, and the phase) and sum them up to compose the QFT.
- The inverse QFT is the same as the QFT except you have to use -1 in the FFT instead of +1, and you use a different phase (the negative of the value for QFT) when you write out the inverse QFT in summation form.