Chris Pollett > Students > Dhole
Print View
[Bio]
[Blog]
[Deliverable #1: Naive Bayes Classifier]
[Hierarchical Agglomerative Clustering - PDF]
[Deliverable #2: Hierarchical Agglomerative Clustering]
[Deliverable #3: Classifiers and Clustering in Yioop]
[Deliverable #4: Recipe plugin scale out]
Naive Bayes Classifier For Email Spam Classification
Aim
To implement Naive Bayes Classifier from scratch to classify Email Spams.
Introduction
In machine learning, naive Bayes classifiers are a family of simple probabilistic classifiers based on applying Bayes' theorem with strong (naive) independence assumptions between the features.
In simple terms, a naive Bayes classifier assumes that the presence (or absence) of a particular feature of a class is unrelated to the presence (or absence) of any other feature. For example, a fruit may be considered to be an apple if it is red, round, and about 4" in diameter. Even if these features depend on each other or upon the existence of the other features, a naive Bayes classifier considers all of these properties to independently contribute to the probability that this fruit is an apple.
Description
My primary task was to understand the Naive Bayes Classifier in Machine Learning and apply it on Email Spams classification
Fork me on GitHub OR Source Code - ZIP
Email spams are manually pulled from spam inbox and pre-classified into 3 classes: 1) I [Internet Advertising] 2) M [Medical Traps] 3) P [Phishing]
We make 2 datasets from the given emails set: 1) Training Data 2) Test Data. On training data, we apply the Naive Bayes Classifier, implemented in Python, and make the classifier model ready. Now, this model is applied on the Training Data and we predict the Class for every spam email. Eventually, we find the accuracy by comparing actual classes and predicted classes.
Data Preprocessing and Data Format:
Given raw data is a flat file, and after processing, it is brought to the format mentioned below:
record number, words, class
e.g. 1, w1, w2, w3, M
2, w3, w4, w5, P
3, w5, w6, w7, I
Functional Overview
NAME
naive_bayes_email_classifier
CLASSES
Tuple
class Tuple
| This is tuple class, whic holds the data in the format of
| doc_id,feature1,feature2,....,class
|
| Methods defined here:
|
| __init__(self)
|
| getClass(self)
|
| getFeatures(self)
|
| getId(self)
|
| setClass(self, cls)
|
| setFeatures(self, txt)
|
| setId(self, id)
|
| show(self)
|
| ----------------------------------------------------------------------
| Data and other attributes defined here:
|
| cnt = 1
FUNCTIONS
evaluateAccuracy(test_tuples, posterior)
This function calculates accuracy
filterClasses(training_tuples)
This generates unique classes that are possible in the given dataset
generateLikelihood(training_tuples, vocab, classes)
This function returns likelihood
generatePrior(training_tuples, classes)
This function returns prior
getVocab(training_tuples)
This function generate unique words from the given text in all tuples
loadData(training_data)
This is a function, which loads the data from file into array
main()
#------------MAIN------------
predict(test_tuples, classes, prior, likelihood)
This function calculates max a prior for every test record
and returns hash of records as doc => prediction
showResults(training_data, test_data, posterior)
This function shows the training data, test data and predictions
Training Data Snapshot
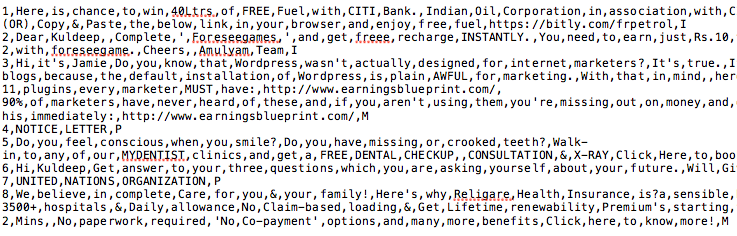
Test Data Snapshot
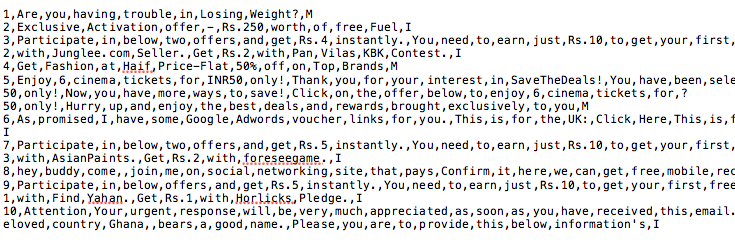
Output Snapshot
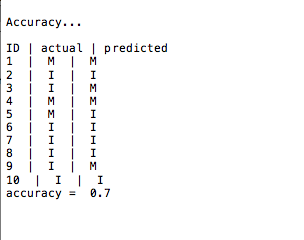
Fork me on GitHub OR Source Code - ZIP