Combinational Circuits
Externally, a logic circuit is a simple input-output device:

Of course there can be any number of input wires and any number of output wires.
The input and output values are always either 0 (low voltage) or 1 (high voltage).
Internally, a logic circuit is implemented as a network of logic gates connected by wires.
Logic circuits divide into two neat categories: combinational circuits and sequential circuits.
A combinational circuit has no memory of previous inputs, while a sequential circuit does. The memory capacity of a sequential circuit (measured in bits, bytes, kilobytes, etc.) determines how far back its memory stretches.
Since a combinational circuit has no memory of previous inputs, the output at time t is completely determined by the input at time t. In other words, given the same input on two different occasions, we would expect the same output.
This is not true for a sequential circuit because the output at time t depends on the input at time t and the contents of memory. In other words, the output at time t depends on the inputs at times t, t – 1, t – 2, etc.
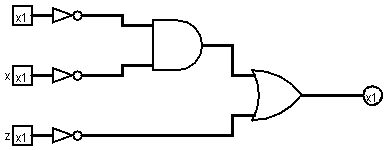
Boolean Logic
The inputs to a combinational circuit above (D) are x, y, and z and the outputs are a, b, and c. There are eight possible inputs to D:
x y z
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
If we focus on just one output, say b, then each of these inputs will cause the value of b to be either 0 or 1. For example:
x y z =>
a b c
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 0
We can think of b as a function of x, y, and z:
b = F(x, y, z)
If we identify 0 with the Boolean value FALSE and 1 with the Boolean value TRUE, then it turns out that F can be represented by a Boolean expression.
We can quickly develop a Boolean expression from a table by forming a disjunction of all combinations of rows that produce a value of 1:
(!x && !y && !z) || (!x && !y && z) || (!x && y && !z) || (x && !y && !z) || (x && y && !z)
After simplifying the expression:
(!x && !y || !z)
We can build a circuit: