Examples

Combinational Circuits

N-bit Components

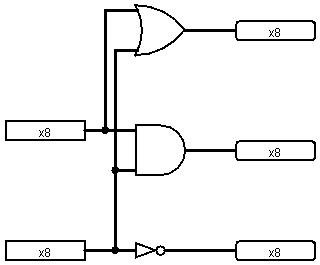
It's easy to construct n-bit analogs of the basic logic gates:

Half Adder

A 1-bit half adder computes the sum of two input bits and a carry-out bit:

s = !a&&b || a && !b

cout = a && b

Full Adder

A 1-bit full adder computes the sum of three input bits: a, b, and cin. It also computes a carry-out bit:

s = !a && !b && cin || !a && b && !cin || a && !b && !cin || a && b && cin

cout = a && b && cin || a && b && !cin | a && !b && cin || !a && b && cin

N-bit Adder

It's easy to construct an n-bit adder from a half-adder and n – 1 full adders.

Arithmetic, etc.

Similarly, we can construct n-bit circuits for -, *, /, %, >, <, ==, <=, >=, <<, >>, >>>

Multiplexer (MUX)

An m-bit control input selects one of 2^m data inputs as output. Inputs and outputs can be n-bits wide.

De-multiplexer (DMX)\

An m-bit control input selects one of 2^m data ouptputs to route its input to. The inputs and outputs can be n-bits wide.

Decoder

A decoder is similar to a de-multiplexer, except a 1 is placed on the selected output wire.

Sequential Circuits

Flip-Flops

Set-Reset S-R

clocked S-R

Delayed

Toggles

Sequence Detectors

Counters

Registers

RAM/ROM