Chris Pollett >
Students >
Shen
( Print View)
[Bio]
[Blog]
CS 297
Deliverables
CS 298
CS297 Deliverable 2
Document-Level Machine Translation with Hierarchical Attention
Experiments with statistical machine translation
Yu-Tang Shen (yutang.shen@sjsu.edu)
Advisor: Dr. Chris Pollett
[PDF version of this page] [Implementation code]Introduction on Statistical Machine Translation
While rule-based machine translation (RBMT) was thriving from 1930s to 1950s, Warren Weaver proposed an idea of utilizing statistics in languages to produce translations [1]. Although RBMT could provide satisfying translation, it required complex rule definition, pre-editing, and post-editing. In contrast, statistical machine translation (SMT) proposed to simply look at the relationship between the statistics of the source language (SL) and the probability of all the possible candidates in target language (TL). With SMT, it was not necessary for programmers to define every single rule between SL and TL, instead, the task became gathering abundant amount of data to obtain an unbiased statistic for every word.
To mathematically describe SMT task, the job can be described as find the best candidate \( \hat t \) for the source language vocabulary \( s\) from the TL distribution \( T\).
$$\hat t = argmax_{t \in T} P(t|s)$$
With more complicated model, which will be covered in section II, parameters \(p\) will be added to the equation to improve the translation quality.
$$\hat t = argmax_{t \in T} P(t|s; p)$$
Statistical Machine Translation Types
There are various designs in SMT, including implementation from Charniak [2], IBM [3], etc.
Greedy algorithm
Greedy algorithm, as the name suggests, chooses the best candidate based on its perspective and disregards all other information. A simple greedy algorithm can be described as follows:
1 translate(S) 2 result = NULL 3 for s in S 4 candidates = getCandidate(s) 5 bestCandidate, bestScore = NULL, -1 6 for candidate in candidates 7 if(probability(s, candidate) > bestScore) 8 bestCandidate = candidate 9 bestScore = probability(s, candidate) 10 end if 11 end for 12 result = result + bestCandidate 13 end for 14 return result
In translate, the algorithm first retrieves all the candidates for the vocabulary s in the given input sentence S, then compare the probability of word s translated into candidate for all candidates.
There are several disadvantages in this method, such as overlooking information in adjacent words, TL ordering, and TL usages. This method merely considers the probability of given SL word translated into some TL word, which completely ignores words' neighbors, which two or more of them can become a phrase. Another common issue in machine translation is the output ordering, for example, TL grammar dictates that subjects should be in front of verbs, while verbs go before subjects in SL grammar. The greedy method preserves the original ordering SL and can fail to reorder the words to produce a grammatically correct TL sentence.
Still, this method provides a more concise way to build a simple machine translator, where rules need not to be specified.
Charniak's model
In Charniak's SMT model, more information is considered when choosing the best candidate for a translation. In Charniak's model, not only the relationship between SL and TL is considered but also the usage of the TL [2].
Charniak developed an English parser that describes the probability of specific word being which part of speech [4]. For example, given a word "said", the probability of it being followed by two consecutive nouns is low, while for the word "gave" the probability of it being followed by two consecutive nouns is high. This parser describes the usage of a language; in other words, it is easy to lookup if a word is used correctly by its probability.
With this parser that describes a language, Charniak utilizes it to optimize the selection process during SMT. As described in the first section, SMT selects best candidate by \(\hat t = argmax_{t \in T} P(t|s)\), and Charniak expanded this formula to \(\hat t = argmax_{t \in T} P(s|t)P(t)\). Since the distribution of \(P(s)\) is fixed once the input is given, two equations are equivalent. Recall that the parser is a function that gives the probability of a given word being which part of speech, the parser serves as \(P(t)\)in Charniak's SMT implementation.
Yamada and Knight [5] published a translation model that takes an English parsing and outputs a translated Chinese sentence. Charniak reversed the process to improve the translation quality from Chinese to English. Instead of retrieving a Chinese sentence from an English parsing, all possible parsing that can yield the input Chinese sentence are retrieved. Charniak's SMT model then search among all the possible parsing for the highest probability. For example, a given Chinese sentence "你好嗎" can be the result from these parsing: "you good", "how are you", "how do you", etc., in Charniak's parser, P("how are you") should have the highest probability, making it the final output of the model.
Experiment
A modified version of greedy SMT is implemented in this report, where in addition to considering the relationship between SL and TL, the adjacent words information and ordering issue are explored.
In this experiment, English to Chinese mapping is retrieved from Taiwan Panorama organized by National Academy for Educational Research, and the usage of Chinese is obtained from [6]. After lemmatizing the input data, the core translation function can be abstracted as follows:
1 translate(S) 2 result := get_current_translation(S) 3 for i in S.length 4 //maximize the probability on both SL-TL mapping and TL usage 5 result[i] := argmax_prob(result[i-1], word, result[i+1], dictionary) 6 end for 7 for i in result.length 8 // swap if two TL words gives a higher probability when flipped 9 if(TL_prob(result[i] + result[i+1]) < TL_prob(result[i+1] + result[i]) 10 result[i], result[i+1] := result[i+1], result[i] 11 end if 12 end for 13 return result
In the beginning, the model will check if there is an available translation to improve on, and when the SL sentence is not available, it simply translates the input by considering the SL-TL relationship. With an initial translation to work on, the model does the following:
$$argmax_{t \in T} P(t_i|s_i) + P(t_{i-1}, t_i, t_{i+1})$$
The former term describes the probability of a SL word \(s_i\) being translated into the TL word \(t_i\), and the latter term defines how probable [\(t_{i-1}\) (the TL word before \(t_i\)), \(t_i\), \(t_{i+1}\)(the TL word after \(t_i\))] is in TL usage.
To address the ordering problem, the program examines if swapping items in bigrams increases the bigram probability in TL usage in the loop in line 7. To describe line 7 mathematically, the loop can be illustrated as:
$$argmax_{\pi = [t_i, t_{i+1}] \in T} P(\pi)$$
The function translate is repeated multiple times until the probability stops increasing.
Two additional experiments are tested to improve translation quality: translate to empty and translate based on TL usage.
Translate to empty
If a SL word can mean an empty string, there will be a slight probability translate selects empty string regardless SL-TL probability and TL usage. Still, this selected translation will compare with all the other translations to ensure that this translation indeed improves the quality.
Translate based on TL usage
With a slight probability, TL candidates can be selected in the following manner: given the previous translated TL vocabulary \(t_{i-1}\), look at the TL usage and select the most common word that follows \(t_{i-1}\), and make it the translation of \(s_i\).
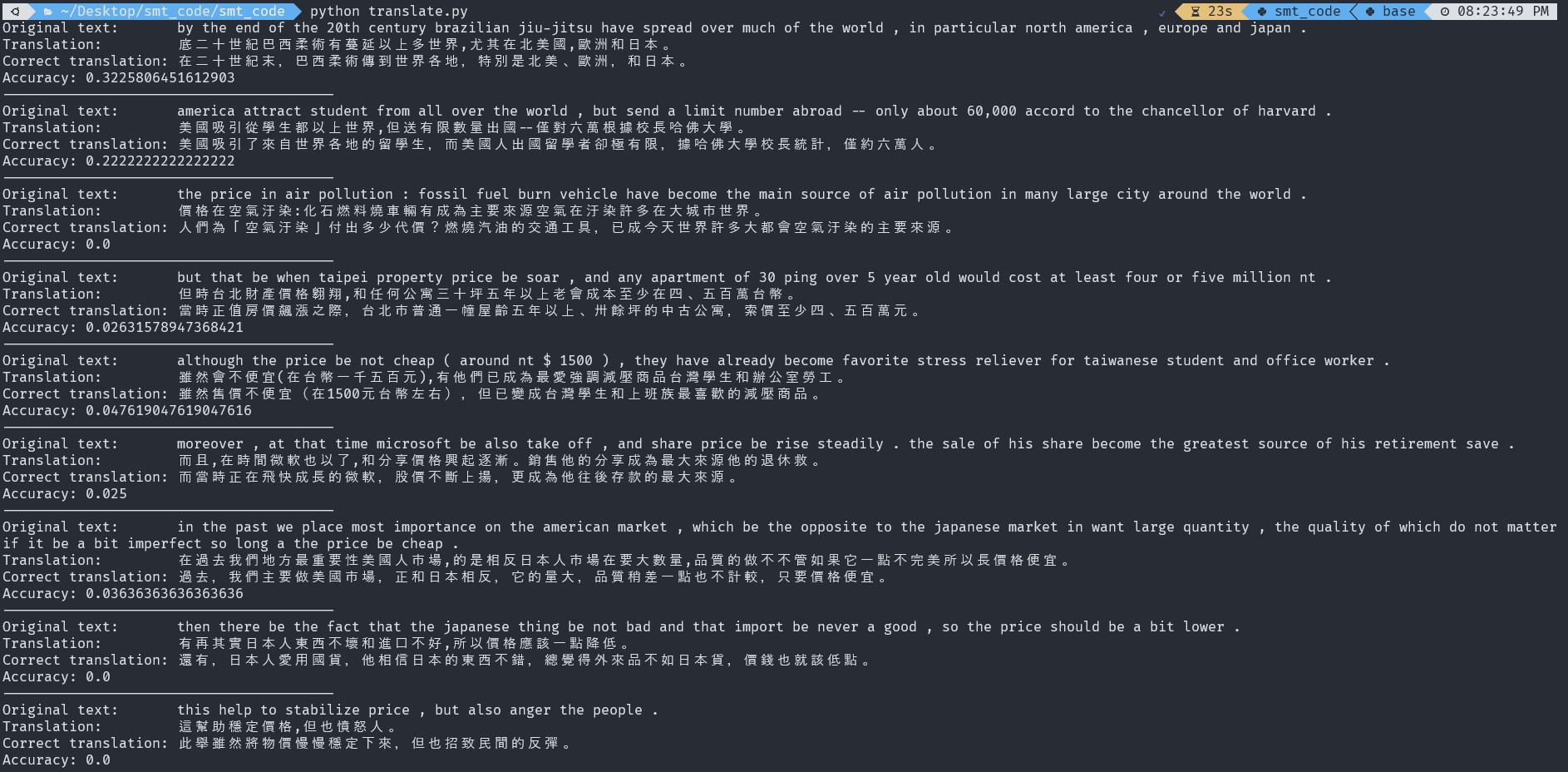
The translation accuracy is measured by simply comparing the prediction with the ground truth divided by the translation sentence length. The accuracy is within the range of 32% to 0%, but most of the results can convey the meaning of the original SL sentence.
Conclusion
SMT provides an easier way to implement machine translation compared to RBMT. SMT selects the most suitable translation over the TL space by considering either SL statistics, TL statistics, SL-TL mapping, or all of them.
In the experiment section, it shows that it is more powerful than RBMT, where it can translate more sentences without manually adding all the underlying rules and the ability to produce a more grammatically correct order. Still, translation quality from SMT is not optimal, as seen in the experiment in this report, and more advanced technique should be used to capture the complex transition from one language to another.
References
- [1] W. J. Hutchins, "Machine translation: A brief history," in Concise history of the language sciences, Elsevier, 1995, pp. 431-445.
- [2] E. Charniak, K. Knight and K. Yamada, "Syntax-based language models for statistical machine translation," in Proceedings of Machine Translation Summit IX: Papers, 2003.
- [3] P. Brown, V. Della Pietra, S. Della Pietra and R. Mercer, "The Mathematics of Statistical Machine Translation: Parameter Estimation," Computational Linguistics, vol. 19, pp. 263-311, 1993.
- [4] E. Charniak, "Statistical Techniques for Natural Language Parsing," AI Magazine, 1997.
- [5] K. Yanada and K. Knight, "A decoder for syntax-based statistical MT," ACL '02: Proceedings of the 40th Annual Meeting on Association for Computational Linguistics, 2002.
- [6] T. Emerson, "The Second International Chinese Word Segmentation Bakeoff," in Proceedings of the Fourth SIGHAN Workshop on Chinese Language Processing, 2005.