GNUchess program's PVS Algorithm

Description: Researched and understood how PVS algorithm works in GNUchess program. In order to understand the algorithm I implemented the Alpha-Beta cutoffs algorithm and Principal Variation Search algorithm and ran it on sample input values.

Figure 1: Sample gametree for comparing Alpha-Beta and PVS algorithm.

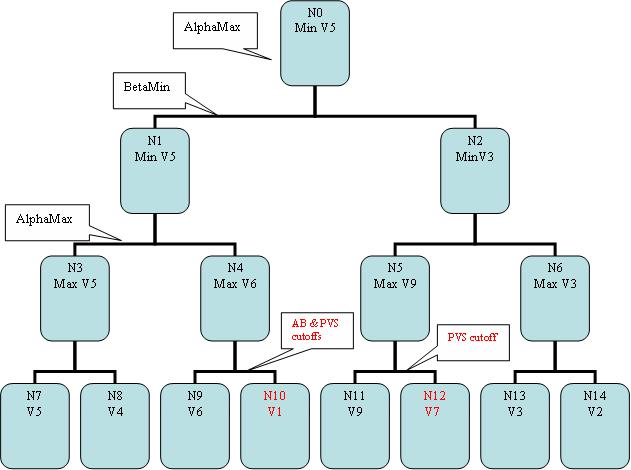
Example 1:Output generated by Alpha-Beta cutoffs program:

In regular minimax, all nodes would have been visited. Total number of nodes = 15
In AlphaBeta, the number of nodes visited is 14. Cutoff occurred at node N4 because the alpha value (6) was greater than the beta value (5). Node N10 was cut off.

Example 2:Output generated by PVS program:

For the same gametree, the number of nodes visited using PVS is 13.
Cutoff occurred at N4 (N10 was cutoff) and also at N5 (N12 was cutoff).
N10 was cutoff due to basic alpha beta pruning.
N12 was cutoff due to PVS algorithm. This cutoff occurred since at N5 alpha 9 >= beta 6. PVNode with a value of 9 was assumed at N5. Since N13 and N14 were also less than 9, this assumption proved to be right.

However, if the following values are put into the tree:
N12 = 10
N13 = 11
N14 = 11

In this case, N12 = 10, would be the final PVS value at N0.
N14 would be cutoff since at N6 alpha 11 >= beta 10.

So, when PVS finds that minimax at node N6 = 11, it knows that the previous assumption of cutting off N12 = 10 was incorrect. So, it has to now search N12 with alpha = 9, beta = 2147483647 score = 10.

The above example illustrates two important things:

• If move ordering is good, PVS usually does better than alphabeta. More nodes can be cutoff. (In the example tree, one extra node was cutoff).
• If the move ordering is not so good, PVS might have to re-search some of the subtrees incurring performance penalty. In any case, PVS will not search any more nodes than alpha beta, but it might have to re-search some of the subtrees like the example with the changed values mentioned above.

Output generated by GNUchess program with my printfs showing tree depths, scores, Alpha Beta values and PV Nodes.

Example 3: Move 1

Initial RootPV = 3299
The RootPV did not change till depth 10 since the computer did not find a better move than what it thought initially. So, it chose d5

Example 4: Move 2

Initial RootPV = 4013.
The RootPV changed to 3690 in between since the computer found a better move than the initial move. (changed from Nf6 to Nc6)

The computer initially generates a PVRoot and the rest of the moves from the hash table. These moves are generated based on the scores by the Evaluate() function.
The evaluate function calculates the score based on such formula:
c1 * material + c2 * mobility + c3 * king safety + c4 * center control + ...
Evaluate() -> Calls all below routines plus a bunch of other criteria ScoreP, ScoreN, ScoreB, ScoreR, ScoreQ, ScoreK

In the above case, till depth 6 (ply=6), the computer could not find a high score for the set of moves and it still had time to think of new moves. It generated a new move (Nc6) for which the new score returned was better than the current best and also better than alpha.
(score > best) && (best > alpha)

This move (Nc6) became the new RootPV.
SearchRoot: RootPV changed. OldRootPV = 4013, NewRootPV = 3690. score = -20, alpha = -26
The computer then generated new moves from the hash table and calculated the minimax scores for them. At depth9, a maximum possible score was attained for this RootPV. So, this move (Nc6) was chosen.
SearchRoot score = -32768. Idepth = 9, RootAlpha = -99, RootBeta = 51, RootPV = 3690

Example 5: Move 3

In this case FAIL HIGH is hit. A score > Beta was returned. The alpha-beta windows had to be readjusted (RootAlpha = 38, RootBeta = 32767) and search had to be done in a regular alpha beta manner. However the final move did not change.

Example 6: Move 4

In this case FAIL LOW case is hit. A score < Alpha was returned. The alpha-beta windows had to be readjusted (RootAlpha = -32767, RootBeta = 1177) and search had to be done in a regular alpha beta manner. However the final move did not change.

Example 6: Final move.

The computer got a very good score at Idepth = 1. It did not have to search beyond that

PVS Code

/*
 * chess.h has the node struct and the gametree defined
 */
#include "chess.h"

/*
 * PVS algorithm with alphabeta
 */
static int
minimaxAB(struct node *n, int a, int b)
{
	boolean_t fFoundPv = FALSE;
	int newb;
	int val;
	int newa;

	if (n->child == NULL) {
		return n->value;
	}
	n->alpha = INT_MIN;
	n->beta  = INT_MAX;
	if (n->knd == Min) {
		struct node *r;
		for (r = n->child; r != NULL; r = r->sibling) {
			newb = MIN(b, n->beta);
			if (fFoundPv == TRUE) {
				printf("Calling1 minimaxAB with Minimal Window %d %d\n",
					a, a+1);
				val = minimaxAB(r, a, a + 1);
				if ((val > a) && (val < newb)) {
					val = minimaxAB(r, a, newb);
				}
			} else {
				val = minimaxAB(r, a, newb);
			}
			printf("minimax at node %s, alpha = %d, beta = %d score = %d\n",
				r->name, a, newb, val);
      		n->beta = MIN(n->beta, val);
			if (a >= n->beta) {
				int nline = FALSE;
				if (r->sibling) {
					printf("\nCUTOFF for %s because alpha %d >= beta %d\n",
						n->name, a, n->beta);
					nline = TRUE;
				}
				for (r = r->sibling; r != NULL; r = r->sibling) {
					printf("Nodes cutoff: %s\n",
						r->name);
				}
				if (nline == TRUE) {
					printf("\n");
				}
				break;
			}
		}
		return n->beta;
	} else {
		struct node *r;
		for (r = n->child; r != NULL; r = r->sibling) {
			newa = MAX(a, n->alpha);

			if (fFoundPv == TRUE) {
				printf("Calling2 minimaxAB with Minimal Window %d %d\n",
					newa, newa + 1);
				val = minimaxAB(r, newa, newa + 1);
				if ((val > newa) && (val < b)) {
					val = minimaxAB(r, newa, b);
				}
			} else {
				val = minimaxAB(r, newa, b);
			}
			printf("minimax at node %s, alpha = %d, beta = %d score = %d\n",
				r->name, newa, b, val);
			if (val > n->alpha) {
				printf("Found PVNode. val = %d, alpha = %d, beta = %d\n",
					val, n->alpha, b);
				n->alpha = val;
				fFoundPv = TRUE;
			}
			if (n->alpha >= b) {
				int nline = FALSE;
				if (r->sibling) {
					printf("\nCUTOFF For %s because alpha %d >= beta %d\n",
						n->name, n->alpha, b);
					nline=TRUE;
				}
				for (r = r->sibling; r != NULL; r = r->sibling) {
					printf("Nodes cutoff: %s\n",
						r->name);
				}
				if (nline == TRUE) {
					printf("\n");
				}
				break;
			}
		}
		return n->alpha;
	}
}
int
main()
{
  int val;

#if 0
  printNode(game1);
#endif
  val = minimaxAB(game1, INT_MIN, INT_MAX);
  printf("\nPVS Alpha Beta Minimax at root position %s is: %d\n",
  	game1[0].name, val);
  return 0;
}