Outline

• Boolean Circuits
• Quiz
• P/Poly
• Logspace Uniformity
• Karp-Lipton Theorem

Boolean Circuits

• Boolean circuits are a more succinct way to represent Boolean functions than Boolean formulas (aka Boolean Expressions).
• Boolean circuits allow us to reuse computations we have already done. For example:
  

Boolean Circuits Formal Definition

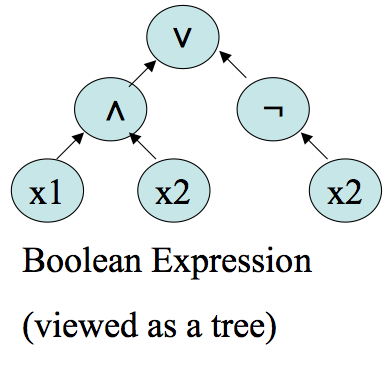
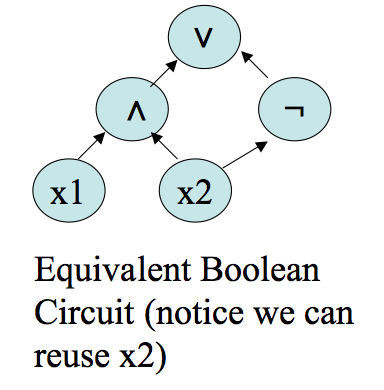
Definition. A Boolean circuit is a directed, acyclic, labeled graph `(V, E, s)`, where `s:V ->{mbox(set of labels)}`. We assume the vertices are numbered `1, ...,n`. All vertices in the graph have indegree `0`, `1`, or `2`. Those of indegree `0` are called inputs and are labeled with variables or true or false. Those of indegree 1 are must be labeled with `neg` and those of indegree 2 can be labelled with `vv` or `^^`. We require the inputs `j`, `k` to any gate `i` be such that `j < i`, `k < i`. Gate `n` is called the output and has outdegree `0`.

• To figure out the output of a circuit for a given truth assignment to the input variables we can evaluate the circuit from the lower numbered gates to the higher numbered gates using the usual rules for `vv`, `^^` , `neg` at each gate.
• This procedure can be implemented in polynomial time. Given a circuit with all of its inputs assigned a value, the problem of determining the output is called the CIRCUIT VALUE PROBLEM (CVP). So we have:
  Proposition. `CVP in P`.
• In contrast, the problem of determining whether a given circuit is satisfiable (`mbox(CIRCUIT-SAT)`) is not known to be in polynomial time.
• Given that `CVP in P` it follows that `mbox(CIRCUIT-SAT) in NP`. On the other hand, as any Boolean formula is a circuit and satisfiability for Boolean formulas is `NP`-hard, we have that `mbox(CIRCUIT-SAT)` is `NP`-hard. Hence,
  Proposition. `mbox(CIRCUIT-SAT)` is `NP`-complete.

Quiz

Which of the following statements is true?

1. AP is contained in NP.
2. It is possible that `Sigma_i^p = Pi_i^p` but for `j geq i` that `Sigma_j^p != Pi_j^p`.
3. `TISP(n^(12), n^(2)) subseteq Sigma_2TIME(n^8)`

Polynomial Size Circuits

• The size of a circuit is the number of gates in it.
• We next would like to define what it means for a family of circuits to recognize a language:
  Definition. A family of circuits is an infinite sequence `(C_0, C_1, ... )` of Boolean circuits, where `C_n` has `n` input variables. We say a language `L` has polynomial size circuits, if there is a polynomial `p` such that `SIZE(C_n) < p(n)` and `C_n` accepts exactly those strings in `L` of length `n`.
• We call the class of languages with polynomial circuits `P``/poly`.

Example

Consider `L = {1^n| n in NN }`.

This language is recognized by the circuit family `F= {C_n}` where `C_n = ^^_{i=1}^n x_i`.

P is in P/Poly

Theorem. All languages in P have polynomial size circuits.

Proof. Let `L in P` be decided by `M` in `n^k` time. WLOG, we can assume `M` uses only one tape. We construct circuits `C_n` such that for `x` such that `|x| = n`, `C_n(x) = 1 iff x in L`. The inputs to this circuit will be `n` variables `x_1, ..., x_n` representing the bits of `x`. We imagine we encode configurations of a TMs as binary strings representing `(`squares seen so far to left of head, state, squares seen so far to right of tape head (or input squares not seen)`)`. The circuit computes from the input string a start configuration of `M`. It then consists of `n^k`-layers, where the `i+1`st layer computes the configuration one would be in given the `i`th layer's configuration. Finally, we take the last layer and have a circuit which computes from it the output of the TM. The total size of this will be `O(n^(2k))`.

Corollary. CVP is `P`-complete under logspace reductions.

Proof. Suppose `L in P`. To reduce `x in L`? to `CVP` we compute the circuit of the last theorem, then we hard code the input bits to be `x` and ask the result to CVP. one can verify this can be computed in logspace.

P/Poly contains Non-recursive Languages

• Consider the language: `L = { y | |y|=n \mbox{ and } n in HALT}`.
• If `L` were decidable then HALT would be decidable: If we want to know if a string `n` is in HALT we could just write down `0^n` and ask if it was in `L`.
• On the other hand, let `phi_n` be the circuit `vv_{i=1}^n(x_i) vv neg vv_{i=1}^n(x_i)`. This circuit (it is even a formula) is always 1 on string of length `n`.
• Similarly, `neg phi_n` is always 0 on strings of length `n`.
• Both `phi_n` and `neg phi_n` are polynomial size in n.
• A P/poly circuit family for `L` consists of `{F_n}` where `F_n = phi_n`, if `n in HALT`, and `F_n = neg phi_n`, otherwise.

Uniformity

Definition. We call a circuit family `(C_0, C_1, ... )` logspace-uniform if there is a `(log n)`-space machine `N` which on input `1^n` outputs `C_n`. We say that a language `L` has logspace-uniform polynomial circuits if there is a uniform family of p-size circuits that decides `L`.

Theorem. A language `L` has logspace-uniform polynomial circuits iff `L` is in `P`.

Proof. One direction follows from the theorem of two slides back, completeness of CVP was logspace computable. For the other direction suppose that `L` has logspace-uniform polynomial circuits. In p-time we can decide `x in L` by first running the logspace machine to get `C_(|x|)` then doing circuit evaluation on `x` in p-time.

Advice Classes

• An advice string is a map from positive integers to strings.
• We say a machine `M` decides a language `L` with advice string `A(n)` if `x in L` implies `M(x, A(|x|))` accepts. And if `x` is not in `L` then `M(x, A(|x|))` rejects.
• Let poly denote the set of advice strings `A(n)` such that `|A(n)| < p(n)` for some polynomial `p(n)`.
• We say a language `L` is in `P``/poly` if there is a a p-time `M` that decides `L` using an advice string in poly.
  Proposition. This and our previous definition of `P``/poly` are equivalent.

  Proof. Notice given `n` the encoding of a a circuit `C_n` is polynomial size and could serve as advice to a machine that essentially computes the value of the circuit on an input. This shows the circuit version of `P``/poly` is contained in the advice version. On the other hand, we can hard-code an advice string as part of the inputs to a circuit `C_n` simulating M(x, y) on inputs on of length `n`. This shows the advice version is contained in the circuit version of this class.

Karp-Lipton

Theorem (K-L 80). If `NP subseteq P``/poly`, then `PH = Sigma_2^p`.

Proof. If suffices to show that `Pi_2^p = Sigma_2^p`. In particular, to show that `Pi_2`-SAT is contained in `Sigma_2^p`. Let
`forall u in {0,1}^n exists v in {0,1}^n phi(u,v)=1`
be an instance of `Pi_2`-SAT. Here `phi` is a Boolean formula.

If `NP subseteq P``/poly`, then there exists a circuit family `{C_n}` of size some polynomial `p` such that for every boolean formula `phi` and `u in {0,1}^n`, `C_n(\phi, u) = 1` iff there exists a `v in {0,1}^n` such that `phi(u,v) = 1`. As stated this circuits solves the SAT decision problem for `phi`. As we showed on Mar 1, we can take such a family of `C_n`'s and modify them so that they actually output the witness `v`. Call this new family of circuits `{B_n}`. The size of `{B_n}` will also be bounded by some polynomial `q` and encoding of such a circuit as a string can be bounded by `10q(n)^2`. Our `Sigma_2^p` essentially guesses such a circuit and verifies that it works. i.e., it checks the following formula: `exists w in {0,1}^(10q^2)forall u in {0, 1}^n mbox(s.t. w describes a circuit B and ) phi(u,B(phi, u)) = 1.`