INDSET

Recall `mbox(INDSET)` (aka INDEPENDENT SET) was the language:
`mbox(INDSET) = {langle G,k rangle | G mbox( has an independent set of size ) k}`

Theorem. `mbox(INDSET)` is `NP`-complete.

Proof. `mbox(INDSET)` is in `NP` since if we guess a subset of `k` nodes of `G` we can in `p`-time verify whether they form an independent set by looking at the encoding of the edgeset to see if each edge between pairs of points in the `k` nodes (quadratic in `k` many look ups). To show `mbox(INDSET)` is `NP`-complete we reduce `3SAT` to it. Let `^^ C_i` be an instance of `3SAT` where each `C_i` is a clause. There is exactly one assignment of the variables in a given `C_i` which will make it false. For each clause, we make a clique out of seven vertices each vertex labelled with the name of the clause and a satisfying true assignment for that clause. For any given clause at most one of these vertices can be in an independent set. To this initial graph we then add edges between vertices in cliques corresponding to different clauses if the assignments on the vertices labels conflict. Finally, if our input `3SAT` instance has `m` clauses, we ask if the resulting graph has an independent set of size `m`. This reduction is at most quadratically larger than the input instance and computationally easy to compute (so p-time). Notice each vertex in such an independent set must belong to a distinct clause-clique of which there are `m`. Further if there is a satisfying for the 3SAT instance, then the values of that assignment in each clause will correspond to a clause-clique vertices that don't share any edges. So in this case, there will be an independent set of size m. Similarly, if there is an independent set of size `m` all of its members must belong to different clause-cliques and there vertex labels must no correspond to conflicting assignments. So from these labels we could read off a truth assignment for the `3SAT` instance.

0/1 IPROG

Recall `mbox(0/1 IPROG)` (INTEGER PROGRAMMING) was the problem: Given a list of `m` inequalities with rational coefficients over `n` variables `u_1`, ..`u_n`, find out if there is a `0`-`1` assignment to the variables that satisfies all the inequalities.

Theorem. `mbox(0/1 IPROG)` is `NP`-complete.

Proof. Given a 0-1 assignment we can check in polynomial time if it works, so the problem is in `NP`. Again, we use `3SAT` to produce our reduction. Let `^^ C_i` be an instance of `3SAT` where each `C_i` is a clause. Given a clause `C_i` we map it to an inequality by mapping a literal `u` to a variable `u` and mapping `bar u` to `(1 - u)`. We then take the sum of these terms and check if its greater than `1`. i.e., if `(u_1 vv bar u_2 vv bar u_3)` was our clause we would map it to the inequality `u_1 + (1 - u_2) + (1 - u_3) ge 1`. We do this for each clause. This can be done in linear time and it is easy to see the resulting program will have a solution iff the original `3SAT` instance could be satisfied.

dHAMPATH

A Hamiltonian Path in a directed graph is a path that visits all vertices exactly once. Let `mbox(dHAMPATH)` denote the set of all directed graphs that contain such a path.

Theorem. `mbox(dHAMPATH)` is `NP`-complete.

Proof. Given a guess of a path in a directed graph, we can check in `p`-time that it visits each node in `G` once and that between any successive pair of nodes in the path, there is an edge. So the problem is in `NP`. Let `phi = ^^ C_i` be an instance of `3SAT` where each `C_i` is a clause. We will map this to a graph `G` with the following properties (1) it has `m` vertices, one for each clause in our `3SAT` instance, (2) it has a special start `v_(mbox(start))` and end vertex `v_(mbox(end))`, and (3) `n` "chains" of 4m vertices corresponding to the `n` variables of `phi`. A chain here is a set of vertices `v_1`, ... `v_(4m)` such that for each `i in [4m -1]`, `v_i` and `v_(i+1)` are connected by by an edge in both directions.

We put edges from the starting vertex `v_(mbox(start))` to points `v_1` and `v_(4m)` of the first chain. We also put edges from the extreme points of the `j`th chain to the extreme points of the `(j+1)`st chain for every `j in [n-1]`. Finally, we put an edge from the extreme points of the `n`th chain to the ending vertex `v_(end)`.

Now to handle the semantics of clauses, for every clause `C` of `phi`, we put edges between the chains corresponding to the variables appearing in `C` and the vertex `v_C` corresponding the `C` in the following way: If `C` contains the literal `u_j`, then we take two neighboring vertices `v_i`, `v_(i+1)` in the `j` chain and put an edge from `v_i` to `C` and from `C` to `v_(i+1)`. If `C` contains `bar u_i`, then we connect these edges in the opposite direction. When adding these edges, we never reuse a link `v_i`, `v_(i+1)`. and always keep an unused link between every two used links. We can do this because our chains have `4m` vertices. Below we can see an image of how this might look...

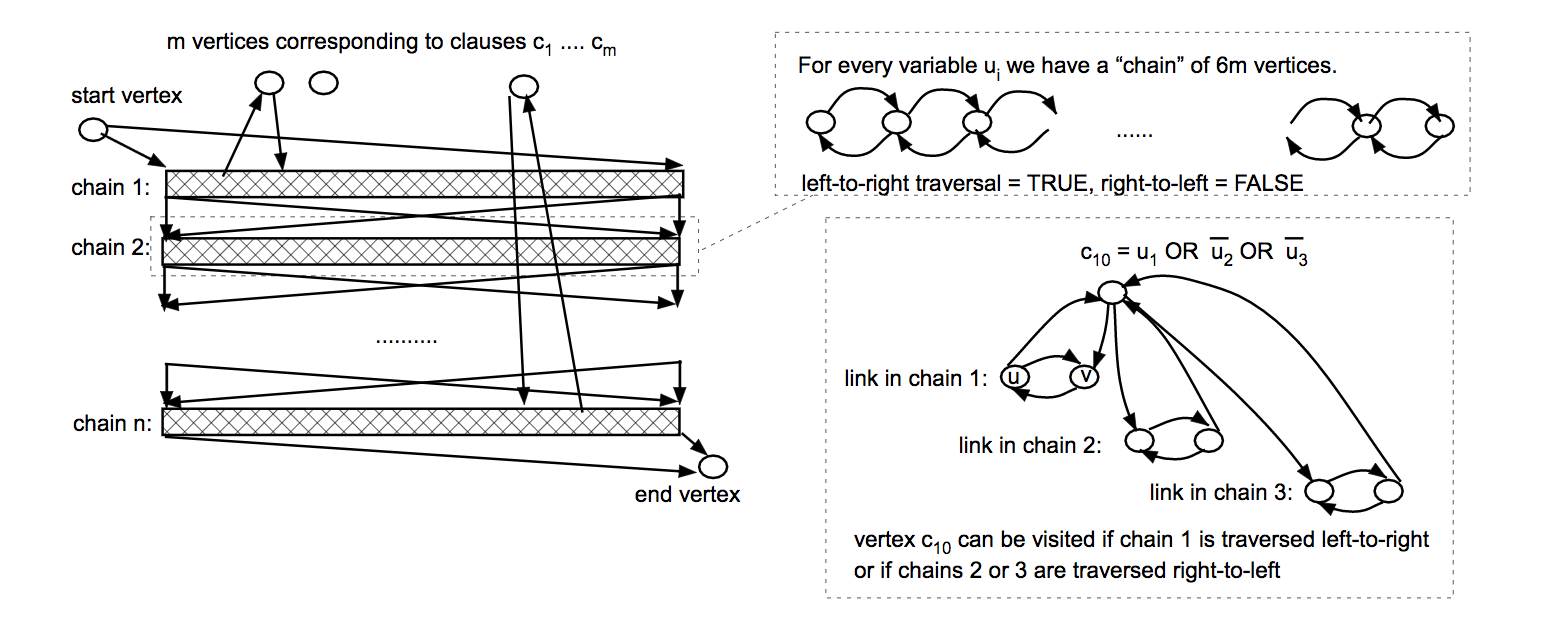
Figure explaining Hamiltonian Path reduction

Finish Completeness proof of dHAMPATH

We now argue `phi in 3SAT iff G in mbox(dHAMPATH)`:

Suppose `phi` has a satisfying assignment `u_1`, ..., `u_n`. Then the path `v_(mbox(start))` traveling through the chains in order and going to `v_(mbox(end))` can be modified into a Hamiltonian cycle. We choose the direction to travel along the `j` chain based on whether `u_i` is `0` (right-to-left) or `1` (left-to-right). If a pair of vertices in a chain is connected to a `v_C` in the correct direction that we haven't yet traversed then we use the pair of edges connecting it to some `v_i` and `v_(i+1)` to traverse it. Since we know there is a satisfying assignment we know for each `v_C` there is some chain with the direction correct. Suppose on the other hand that we are given a graph `G` from such a construction and we find a Hamiltonian path in it. Since `v_(mbox(start))` is a source vertex and `v_(mbox(end))` a sink, these must be the end points of a the path. Given the construction each chain in the path can be traversed in exactly one direction, so from this we can read off an assignment to the variables. Finally, the fact that such a path must traverse each `v_C` shows that how this assignment will witness each clause.

In-class Exercise

Consider the formula `x_1 ^^ \neg x_1`. Draw a picture of the graph corresponding to this under the Hamiltonian Graph reduction just given.

Consider the clause set `{{x_1, x_2, x_3},{\bar{x_1}, x_3, \bar{x_4}}}`. Draw a picture of the graph corresponding to this under the Hamiltonian Graph reduction just given, indicate on the graph a Hamiltonian cycle.

Take pictures of your solutions and post them to the Mar 1 Class Thread.

Decision versus Search

Have we sacrificed much by considering decision problems in `NP` rather than `p`-time functions which output the verifier's certificate? The following theorem says no:

Theorem. Suppose `P=NP`. Then for every `NP`-language `L` and verifier TM `M` for `L`, there is a polynomial-time TM `B` that on input `x in L` outputs a certificate for `x`.

Proof. We need to show that if `P=NP`, then for every `p`-time TM `M` and polynomial `p(n)`, there is a `p`-time TM `B` with the following property: for every `x in {0, 1}^n`, if there is `u in {0, 1}^(p(n))` such that `M(x,u) = 1` then `|B(x)| = p(n)` and `M(x,B(x)) = 1`.

We first show the result for `SAT`. Let `A` decide `SAT` in `p`-time. Such an `A` exists since we are assuming `P=NP`. Let `B` work as follows: We first use `A` to check if `phi` is satisfiable. If not, HALT. Otherwise, we set `x_1 = 0` in `phi` and ask if the resulting formula is satisfiable. If it is output `0` so far; otherwise, output `1` so far. Using the value we got for `x_1`, we then set `x_2 = 0` in the formula and ask is the resulting formula satisfiable, and proceed similarly. We continuing querying for each variable of `phi` until we have a complete assignment. `B` runs in linear time in `A` which we assumed to be `p`-time.

To solve the problem for an arbitrary `NP`-language `L`, we use the fact that our reduction of `L` to `SAT` was a Levin reduction. This means that we have a `p`-time computable function `f` such that not only `x in L iff f(x) in SAT` but also we can map a satisfying assignment for `f(x)` into a certificate for `x`. Therefore, we use the above algorithm to come up with an assignment for `f(x)` and then map it back into a certificate for `x`. Q.E.D.

The above uses the property of SAT that if we can solve instances of length less than `n` then we can solve instances of length `n`. This is called downward reducibility.