Outline

• Minimal Description Length
• HW Problem
• Inequalities
• Optimality
• Incompressible Strings

Information

• Today we would like to define a notion of how much information a string contains.
• This is also related to how random a string is.
• This area is useful in the development of pseudo-random number generators which can be used in randomized algorithms and in cryptography.
• It was somewhat independently developed by Kolmogorov (1963, 1965) and Chaitin (1969).

Descriptions via TMs

• Consider the following string:
  `11111111111111111111111111111111111111111111111`
  `11111111111111111111111111111111111111111111111`
  `1111111111111111111111111111111`
• Although it is quite long it is not very random.
• I can quite simply describe it as write hundred and twenty five `1`'s in a row.
• One can make a TM `M` which reads its input in decimal then writes out that many `1`'s.
• If I had wanted a million `1`'s. Then `langle M, 1000000 rangle` would easily be shorter to write down then all these `1`'s.
• This motivates the next definition.

Minimal Description Length

Definition. Let `x` be a binary string. The minimal description of `x`, `d(x)`, is the lexicographical first shortest string `langle M, w rangle` such that `M` on input `w` halts with `x` on the tape. We define `K(x) = |d(x)|`.

Theorem. `exists c forall x[K(x) leq |x| + c]`.

Proof. Let `M` be the machine that halts as soon as it starts. Then `langle M, x rangle` describes the string `x`. The length of `|M|` is some number `c`. From which we get that `K(x) leq |langle M, x rangle| leq |x| + c` as desired.

Some Inequalities Involving Minimal Description Length

Theorem. `exists c forall x[K(\x\x) leq K(x) + c]`.

Proof. Let `d(x) = langle M, w rangle` be a minimal description of `x`. Then `langle N, langle M,w rangle rangle` describes `\x\x`, where `N` is the machine which on input `langle M, w rangle` runs `M` on `w`, then writes the output of the simulation twice.

Using the same kind of idea one can show:

Theorem. `exists c forall x,y [K(xy) leq 2K(x) + K(y) + c]`.

Homework Problems (Sec 1 - 1,2) (Sec 3 - 1, 3)

Problem 1. Consider the machine `M`:

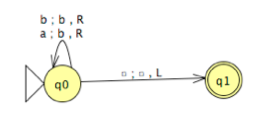
Show the dominos that would be played using the PCP construction to simulate M on aabba.

Answer. First, let's write down the non-starred tiles that we would get based on the Undecidability of PCP proof slide. There are:
{[`#|#q_0\a\a\b\b\a\#`] (Type 1), [`q_0a|bq_0`] (Type 2), [`q_0b|bq_0`] (Type 2),
`\quad` [`bq_0\square|q_1b\square`] (Type 3), [`aq_0\square|q_1a\square`] (Type 3),
`\quad` [`\square q_0\square|q_1\square\square`] (Type 3),
`\quad` [`a|a`] (Type 4), [`b|b`] (Type 4), [`\square|\square`] (Type 4),
`\quad` [`#|#`] (Type 5), [`#|\square #`] (Type 5),
`\quad` [`aq_1 | q_1`] (Type 6), [`q_1a | q_1`] (Type 6),
`\quad` [`bq_1 | q_1`] (Type 6), [`q_1b | q_1`] (Type 6),
`\quad` [`\square q_1 | q_1`] (Type 6), [`q_1 \square | q_1`] (Type 6),
`\quad `[`q_1## | q_1#`] (Type 6) }.

The recipe for making the starred version of the above is to make the first tile into the form: [`star t_1| star b_1 star`] and all other tiles into the form [`star t_i|b_i star`] and finally add a tile [`star\$|\$`]. So in our case the first tile would become:
[`star #|star # star q_0 star \a star \a star \b star \b star \a star \# star`]
and a tile like:
[`aq_0\square|q_1a\square`]
would become:
[`star a star q_0 star \square|q_1 star a star \square star`].
As except for the clutter of stars, the match in the starred version of the problem will look the same as in the non-starred version, we draw the match for the non-starred version. This is given in the following image:

Problem 2. Let `L={langle M rangle | mbox(M is a TM that only accepts inputs of odd length)}`. Carefully use Rice's Theorem to show `L` is undecidable.

Answer. We need to establish about `L` two things to apply Rice's Theorem: (1) There are some `langle M rangle in L` and some `langle M rangle !in L`; (2) If `L(M_1) = L(M_2)` then both either both `M_1, M_2 in L` or both `M_1, M_2 !in L`. To see (1) notice the machine `\R\e\j` which immediately rejects, doesn't accept any inputs. Hence, of the inputs it accepts, they are all of odd length. So `\R\e\j in L`. On the other the machine `M_(00)` which only accepts the string 00 is not in `L`. So condition (1) of Rice's Theorem holds. To see that condition two holds just notice that if two TMs,`M_1` and `M_2` have the same language, then that language either has a string of even length or it doesn't. If it doesn't then both `M_1` and `M_2` would be in `L` and if it does they both would not be in `L`. Hence, condition (2) holds. Since both the prerequisites of Rice's Theorem hold, we therefore have by Rice's Theorem that `L` is undecidable.

Problem 3. Show `L={langle M rangle | mbox(M is a TM that only accepts inputs of odd length)}` is undecidable without using Rice's Theorem.

Answer. We prove this by contradiction. First, let `\R\e\j` be the machine immediately rejects. It doesn't accept any inputs. Hence, of the inputs it accepts, they are all of odd length. Suppose we have a decider `D` for `L`. We give a machine `A` that could then do `A_{TM}` as follows:

A := "On input `langle M, w rangle`:

1. Build the machine '`B:=` On input `x`:
   
   1. If `x` is of odd length reject; otherwise,
   2. if `x` is of even length run `M` on input `w` and accept only if `M` does.'
2. Run `D` on `langle B rangle`, if it accepts, reject; if it rejects, accept.

Notice `A` always halts accepting or rejecting, so will be a decision procedure. Also, `A` only accepts if `B`'s language contains an even length string which in turn can occur only if `M` accepts input `w`. So `A` is a decision procedure for `A_(TM)`. As we know such a procedure does not exist, we therefore conclude, `D` does not exist, which means `L` is undecidable.

Optimality of the Definition

• Our definition is in terms of TMs, would it have made a difference to define minimal description length in terms of C++ programs?
• Let `K_p(x)` be defined in the same way as `K(x)` but using the description language `p`.

Theorem. `forall x[K(x) leq K_p(x) + c]`.

Proof. Consider the machine `M` which on input `langle p', w rangle` simulates the program `p'` in programming language `p` on input `w`, then outputs what that programming language would output. So `langle M, d_p(x) rangle` outputs `x` and this string is at most constantly longer than `K_p(x)`.

Incompressible Strings

Definition. Let `x` be a string. Say that `x` is `c`-compressible if `K(x) leq |x| - c`. If `x` is not `c`-compressible, we say that it is incompressible by `c`. If `x` is not `1`-compressible, we say that it is incompressible.

Theorem. Incompressible strings of every length exist.

Proof. The number of strings of length `n` is `2^n`. Each description is a binary string, so the number of descriptions of length less than `n` is at most the sum of the number of strings of each length up to `n-1`, or `1+2+4+8 + cdots + 2^{n-1} =2^n-1` which is less than the number of strings of length `n`. So some incompressible string of length `n` must exist.

Almost-all Properties and Incompressible Strings

We next show that computable properties that hold for almost all strings hold for all but finitely many incompressible strings. By holds for almost all strings, we mean the fraction of strings of length `n` on which it fails to hold approaches `0` as `n` gets larger.

Theorem. Let `f` be a computable property that holds for almost all strings. Then for any `b > 0`, the property `f` is FALSE on only finitely many strings that are incompressible by `b`.

Proof. Consider the following `M`:

`M = `"On input `i`, a binary integer:

1. Find the `i`th string `s` where `f(s) =` FALSE, considering the strings ordered lexicographically.
2. Output string `s`."

For any string `x`, let `i_x` be the position of `x` on a list of strings that don't have property `f`. So `langle M, i_x rangle` is a description of `x` and it has length `|i_x| + c` where `c= |langle M rangle|`. Fix `b > 0`. Choose `n` such that `1/2^{b+c+1}` fraction of strings of length `n` or less fail to have property `f`. By our definition of "holds for almost all strings" we can find such an `n`. Let `x` be a string of length at most `n` that fails to have property `f` (if it doesn't exists then property `f` holds of all `b`-incompressible strings of length `n` and we're done). As there are at most `2^{n+1} - 1` strings of length `n` or less, so
`i_x \leq (2^{n+1} -1)/(2^{b+c+1}) leq 2^{n-b-c}`.
Therefore, `|i_x| leq n - b - c` so `langle M, i_x rangle` is at most `(n-b-c) +c = n-b` and so `K(x) \leq n -b ` so `x` couldn't have been `b`-incompressible.