Outline

• Dominoes and undecidability
• HW Problems
• Rice's Theorem
• Programs that Print Themselves

Post Correspondence Problem

• We now are going to show that there are problems other than problems for machines which are undecidable.
• We are going to consider problems involving dominos. These are pairs of strings `[s|t]`.
• Given a set of dominoes {[`s_1`|`t_1`], `ldots`, [`s_k`|`t_k`] }. we want to know if we can arrange a subset of them (we allow repeats) so that `s_{i_1}, ldots, s_{i_j} = t_{i_1}, ldots, t_{i_j}`. This is called a match and the whole problem is called Post's Correspondence Problem (PCP).
• For example, given the tiles{ [b|ca], [a|ab], [ca|a], [abc|c]}, the following is a match [a|ab][b|ca][ca|a][a|ab][abc|c].
• We can associate a language to this problem as:
  `PCP = { langle P rangle | P mbox{ is an instance of Post's Correspondence Problem with a match}}`

Undecidability of PCP.

Theorem (Post 1946). PCP is undecidable.

Proof. We show via computation histories that if `PCP` is decidable so is `A_{TM}`, thus giving a contradiction. Given an input `langle M, w rangle` for `A_{TM}` we will construct an instance of `PCP` which will have a match iff `M` accepts `w`. Further, the string of the match which be an accepting computation history of `M` on `w`. To simplify our problem we will consider the following modifications to `A_{TM}` and `PCP`:

1. We assume `M` on input `w` never tries to move left off the tape.
2. If `w = epsilon`, we use the string `square` in place of `w` in the construction.
3. We modify `PCP` to require that a match starts with the first domino.

More Undecidability of PCP

Call the instance of `PCP` that we are building `P`.

1. Put `[#| #q_0 w_1 ldots w_n #]` as the first domino of the `PCP` instance. Playing this domino first will force the string to look like an initial configuration of `M` on `w`.

Next we add dominos to handle the part of the configuration where that the TM might change.

2. For every `a, b` in the tape alphabet, and every states `q, r` of `M` where `q ne q_{mbox{reject}}`, if `delta(q, a) = (r, b, R)`, we put `[qa | br]` into `P`.

3. For every `a, b, c` in the tape alphabet and every states `q, r` in `M` where `q ne q_{mbox{reject}}`, if `delta(q, a) = (r, b, L)`, we put `[cqa | rcb]` into `P`.

Next we add dominos to copy the unchanged parts of configurations and to copy the end of configuration markers

4. For every `a` in the tape alphabet, we put `[a | a]` into `P`.

5. Put `[#|#]` and `[#|square #]` into `P`. (The second is to simulate the case where the size of a configuration grows).

Lastly, we add dominos so that once we get to an accept state, we have a sequence of configurations with an ever smaller number of squares so we can catch up the top row with the bottom row:

6. For every tape symbol `a` we have dominos `[aq_{mbox{accept}} | q_{mbox{accept}} ]` and `[q_{mbox{accept}}a | q_{mbox{accept}} ]` and to complete the match we have `[q_{mbox{accept}}## |#]`

Examples of these Dominos

• Suppose `M` on input `w=0100` starts in state `q_0`.
• Suppose further in this state reading a 0 it goes into state `q_7` writes a `2` and moves right.
• The first five kinds of dominos could be played to get the following partial configuration history:
  

Eliminating the First Domino Condition

• Suppose we have an instance
  `P = {[t_1| b_1],` `[t_2| b_2], ldots, [t_k| b_k]}`
  of `PCP` where we'd like the first domino to be played and we like to make it into a real instance `P^star` of `PCP` without this condition.
• Let `star` and `\$` be new symbols not appearing in the `t_i`'s and `b_i`'s. Given a string `u = u_1 ldots u_n`. Define `star u = star u_1 star u_2 star ldots star u_n`, `star u star = star u_1 star u_2 star ldots star u_n star`, and `u star = u_1 star u_2 star... star u_n star`.
• Then `P^star={[star t_1| star b_1 star], ` `[star t_2|b_2 star], ldots, [star t_k|b_k star], [star\$|\$]}` will have a match in the usual `PCP` iff `P` had a match in the modified `PCP`.

End of the PCP reduction

• So assume we had a decision procedure `D` for `PCP`.
• Consider the machine:
  `S=` "On input `langle M, w rangle`:
  
  1. Construct an instance `langle P^star rangle` of `PCP` following the construction of the last few slides.
  2. Run `D` on `langle P^star rangle`.
  3. If `D` accepts, accept; else if `D` rejects, reject."
  This machine is a decision procedure for `A_{TM}`, which we know cannot exist.
• Therefore, the assumption `D` exists must be false.
• Therefore, `PCP` is undecidable.

Homework Problems (Sec1 - Prob 1,3), (Sec 3 - Prob 1,4)

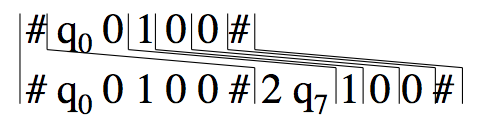
Problem 2 is in the book.

Problem 1. Explicitly write down a function `f:{0,1,2,3,4} -> P({0,1,2,3,4})` of your choice but not the identity function. Then write down the complement of the diagonal for your function.

Answer. By not the identity function, I meant not the function `f(i) = {i}`, so let's consider the following `f` instead:

`f(0) = {0,1}`,
`f(1) = {0,1,4}`,
`f(2) = {1,2,3}`,
`f(3)={0,1,2,3,4}`,
`f(4) ={}`.

Viewing elements of the power set as sequences, this gives the following five sequences:

(1, 1, 0, 0, 0),
(1, 1, 0, 0, 1),
(0, 1, 1, 1, 0),
(1, 1, 1, 1, 1),
(0, 0, 0, 0, 0)

where the diagonal has been bolded. Hence, a complement of the diagonal would be the sequence: (0,0,0,0,1) which corresponds to the set `{4}`.

Problem 3. Define `\mbox{Sub-HALT}_{TM} = { langle M, w rangle | \mbox{M is a TM and there is a substring v of w on which M will halt}}`. Give a many-one reduction of `\mbox{HALT}_{TM}` to `\mbox{Sub-HALT}_{TM}`.

Answer. We want a Turing computable function:

`f: langle M, w rangle mapsto langle M', w' rangle`

such that `langle M, w rangle in \mbox{HALT}_{TM}` iff `langle M', w' rangle in \mbox{Sub-HALT}_{TM}`. First, we can build a machine `f` that on inputs not of the form `langle M, w rangle` is just the identity function (a Turing computable thing to check)-- since the input is not of the correct form, it won't be in either language. Suppose now our machine for `f` has checked the input and it is s in the correct format. Certainly, if langle `M, w rangle in \mbox{HALT}_{TM}` then `langle M, w rangle in \mbox{Sub-HALT}_{TM}` since `w` is a substring of `w`. But it might be the case that `M` on `w` doesn't halt, but there is a substring `v` of `w` on which `M` does halt. However, since `f` is given the string `w` as an input, it can do things like build the machine `M''` which checks whether its input is `w` and if not run forever; otherwise, accept. Let `M'` be the machine that runs `M''`. If `M''` is about to accept, it then runs `M` on input `w`. The map:

`f: langle M, w rangle mapsto langle M', w rangle`

is Turing computable and the only substring of `w` on which `M'` might halt is the string `w`. Further, it halts on `w` iff `M` halts on `w`. Thus, this `f` gives the desired reduction.

Problem 4. Show `\mbox(EQ)_(LBA) = { langle M, M' rangle | \mbox{M and M' are LBAs with the same language}}` is undecidable.

Answer. It suffices to show some undecidable problem is reducible to `\mbox(EQ)_(LBA)` to show `\mbox(EQ)_(LBA)` is undecidable. In this case, we give a reduction from `\mbox(E)_(LBA)` which we showed was undecidable in class. Let `M_2` be the LBA that halts on any input rejecting (this obviously does not need to moves it tape head off its input, so is in fact an LBA). Given an instance `langle M rangle` consider the function:

`f: langle M rangle mapsto langle M, M_2 rangle`.

This function involves tacking a fixed string onto the string `langle M rangle`, so will be Turing computable. If `langle M rangle in \mbox(E)_(LBA)` then `M`'s language is empty and so `M` will have the same language as `M_2` and hence `langle M, M_2 rangle in \mbox(EQ)_(LBA)`. On the other hand, if `langle M rangle !in \mbox(E)_(LBA)` then `M` won't have the same language as `M_2`, so `langle M, M_2 rangle !in \mbox(EQ)_(LBA)`. Therefore, the function `f` gives us the desired reduction from `\mbox(E)_(LBA)` to `\mbox(EQ)_(LBA)`.

PCP Remarks

• The version of PCP where you ask for matches where no more than `k` dominoes are used is NP complete under Karp reductions (Constable, Hunt, Sahni, 1974).
• Post Correspondence Problem (tiling dominoes) has a character similar to other problems such as tiling regions of the plane, etc.
• Hao Wang in the 1960s observing this created what are known as Wang dominoes/tiles, which were square tiles each edge marked with a number. His domino problem was to determine if a set of such dominoes could tile the plane so that tiles sharing an edge have the same number on that edge. Wang in 1961 had shown the problem is decidable iff all instances of the problem either don't tile or are periodic. Wang's student, Berger 1966, showed the problem was unsolvable by exhibiting an aperiodic tiling.
• Raphael Robinson in 1971 reduced the number of kinds of tiles needed in an aperiodic tiling to six, but in so doing made the tiles of an irregular shape.
• Roger Penrose in 1974 introduce the first of his Penrose tilings based on the pentagon which also only needed six tiles. Using a kite shape he was later able to reduce the number of kinds of tiles to two.
• Bounded variants of the tiling problem might seem a lot like the game Tetris. In fact, many problems involving Tetris are known to be NP-hard under Karp reductions (Demaine, et al 2002).
• There has also been some work in using Wang Tiles in computer graphics (Stam 1997, Cohen, et al 2003) and in creating Wang tiles using DNA (Lukeman 2002).

Rice's Theorem

Rice's theorem (Transactions AMS, 1953) shows that almost any problem one could come up with connected to Turing Machines is undecidable.

Theorem. Let `P` be a language such that there exists TM descriptions `langle M rangle in P` and ` langle M' rangle !in P`. Further assume that whenever we have two machines `M_1` and `M_2` such that `L(M_1) = L(M_2)`, then we have `langle M_1 rangle in P` iff `langle M_2 rangle in P`. Then `P` is undecidable.

Proof. Suppose we had a decider `R` for `P`. We show how to use `R` to build a decider for `A_{TM}`. Let `T_{emptyset}` be a TM which always rejects, so `L(T_{emptyset}) = emptyset`. We may assume `T_{emptyset} !in P`; otherwise, we carry out our argument using `bar P`. Because `P` is not trivial there exists a TM `T` with `T in P`. Using this machine consider the following decider `S` for `A_{TM}`:
`S =` "On input `langle M, w rangle`:

1. Use `M` and `w` to construct the following TM `M_w` :
   `M_w =` "On input `x`:
   1. Simulate `M` on `w`. If it halts and reject, reject. If it accepts, proceed to Stage 2.
   2. Simulate `T` on `x`. If it accepts, accept."
2. Use TM `R` to determine whether `langle M_w rangle in P`. If yes, accept. If no, reject."

Example Use of Rice's Theorem

• Consider the language `L={ langle M rangle| M mbox{is a TM and } 1011 in L(M)}`.
• This language contains some, but not all TM encodings.
• It further has the property that for any `M_1` and `M_2` such that `L(M_1) = L(M_2)`, that we have `langle M_1 rangle in L` iff `langle M_2 rangle in L`.
• Therefore, by Rice's Theorem it is undecidable.

Rice's Theorem Remarks

• Several variants of Rice's Theorem have been considered.
• Perhaps, the first was due to Greibach 1966 (Greibach's Theorem):
  Theorem. Let `C` be a class of languages that is effectively closed under concatenation with regular sets and union, and for which `=\Sigma^star` is undecidable for any sufficiently large fixed `\Sigma`. Let `P` be any nontrivial property, that is true for all regular sets and that is preserved under `/a`, where `a` is a single symbol. (That is, if `L` has the property `P`, so does `L``/ a = { w | wa in L }`.) Then `P` is undecidable for `C`.
• Variants of Rice's Theorem within the class NP can be found in Borchert and Stephan 2000 as well as Hemaspaandra and Thakur 2002.
• Connections between Rice's Theorem, program obfuscation, and the existence of one-way functions in cryptography can be found in Barak, et al., 2001.