Outline

• Randomized Walks for 2-SAT
• Quiz
• Randomized Approximation Algorithms
• Linear Programming based Approximation

Introduction

• Last week, we began talking about approximation algorithms for NP-complete problems.
• Given an NP-complete problem, say 3-SAT. We look at the associated optimization problem, in this case, trying to satisfy the most clauses. Then we try to come up with good algorithms for it. I.e., both `p`-time and a good approximation.
• Let `C` denotes our algorithm's solution. For 3-SAT this would be the number of clauses our algorithm satisfies. Let `C^{\star}` denote the best possible value. We defined `max(C/C^{star}, C^{star}/C)` as the approximation ratio of our algorithm.
• We gave p-time, 2-approximation algorithms for VERTEX-COVER and Euclidean TSP, however, we showed that for general TSP, if there was an a `m gt 0` such that it was `m`-approximable in `p`-time then we could solve HAM-CYCLE, and hence, `P=NP`.
• At the end of last day, we considered the SET-COVER problem: Given a set `X` and a set of subsets `F = {S | S subseteq X}` find the size of the smallest cover of `X` in `F`.
• We gave a greedy algorithm to find a set cover and we showed GREEDY-SET-COVER is a polynomial-time `r(n)`-approximation algorithm, where
  `r(n) = H(max{|S| : S in F})` on instances `(X,F)` or size `n`.
• Today, we start by considering a randomized algorithm for 2-SAT before consider randomized approximation algorithms.

Random Walks for SAT

• Consider the following algorithm for satisfiability:
  1. Start with any truth assignment `T`, and repeat the following `r` times:
     1. If there is no unsatisfied clause output "Satisfiable", halt.
     2. Otherwise, take any unsatisfied clause; pick any of its literals at random and flip its value
  2. After `r` repetitions reply "the formula is probably unsatisfiable"
• Is there a good value of `r` to choose so that this algorithm works?

Random Walks for 2SAT

Theorem. Suppose that the random walk algorithm with `r=2n^2` is applied to any satisfiable instance of 2SAT with `n` variables. Then the probability that a satisfying truth assignment will be discovered is at least `1/2`.

Proof. Let `T` be a truth assignment which satisfies the given 2SAT instance `I`. Let `t(i)` denote the number of expected repetitions of the flip step until a satisfying assignment is found starting from an assignment `T'` which differs in at most `i` positions from `T`. Notice:

1. `t(0) = 0`
2. If we find some other satisfying assignment, we do not need to continue.
3. Otherwise, we flip at least once, and we have a 50% chance of moving closer to the solution; 50% farther. So `t(i) le 1/2(t(i-1) + t(i+1)) + 1`
4. We also have `t(n) le t(n-1) + 1` (If every literal is wrong, we can only move closer).

The worst case is the when relation `t` of (3) and (4) hold as equations. `x(0)=0`; `x(n)=x(n-1)+1`; `x(i) = 1/2(x(i-1)+x(i+1))+1`

Proof Cont'd

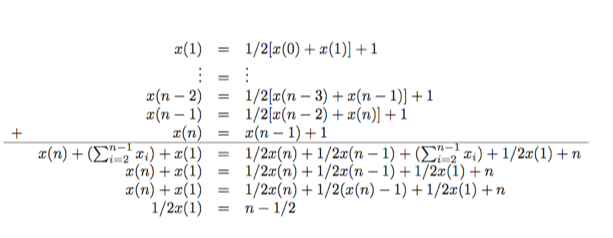
• As you can see above, adding all the `x(i)`'s together gives: `x(1) = 2n-1`.
• Then solving the `x(1)` equation for `x(2)` gives `4n-4`, and in general, `x(i) =2 i n-i^2`.
• Thus we have shown `t(i) le x(i) le x(n)=n^2`. Now consider the following lemma:
  Lemma (Markov Inequality). If `x` is a random variable taking nonnegative integer values, then for any `k > 0`, `Pr[x ge k cdot E(x)] le 1/k`.
  Proof. Let `p_i` be the probability that `x=i`.
  `E(x) = sum_i i cdot p_i = sum_(i le k cdot E(x)) i cdot p_i + sum_(i > k cdot E(x)) i cdot p_i > k cdot E(x) cdot Pr[x>k cdot E(x)]` Q.E.D.
• The theorem then follows taking `k=2`.

Quiz

Which of the following statements is true?

1. Our 2-approximation algorithm for VERTEX COVER made use of minimal spanning trees.
2. We showed if `P ne NP` then there is no p-time approximation algorithm for TSP.
3. We gave an 8/7 approximation algorithm for set cover based on an amortized analysis.

Randomized Approximation Algorithms

• We say a randomized algorithm for a problem has an approximation ratio of `r(n)` if for any input size `n`, the expected cost `C` of the solution produced by the randomized algorithm is within a factor of `r(n)` of the cost `C^star` of an optimal solution.
• We call a randomized algorithm that achieves an approximation ratio of `r(n)` a randomized `r(n)`-approximation algorithm.
• Let MAX-kSAT be the problem of determining given a `k`-CNF formula an assignment which makes as many clauses as possible evaluate to `1`.

Algorithm for MAX-3SAT

Theorem. Given an instance of MAX-3SAT with n variables and `m` clauses, the randomized algorithm that independently sets each variable to `1` with probability `1/2` and to `0` with probability `1/2` is an randomized `8/7`-approximation algorithm.

Proof. Define the indicator random variable `Y_i = I{`clause `i` is satisfied`}`. Since no literal appears more than once in the same clause, and since we assume that no variable and its negation appear in the same clause, the settings of the three literals are independent. A clause is not satisfied only if all three of its literals are set to `0`. We thus have:

1. `Pr{ mbox{clause } i mbox( is not satisfied ) } = 1/8`
2. `Pr{ mbox{clause } i mbox( is satisfied ) } = 7/8`.
3. `E[Y_i] = 7/8`.

Let `Y = sum_i Y_i`. Then
`E[Y] = E[sum_i Y_i] = sum_iE[Y_i] = sum_i 7/8 = (7m)/8`.
As `m` is an upper bound on the number of possible clauses that could be satisfied, this gives the result.

Weighted Vertex Cover

• The minimum-weight vertex cover problem is given a graph `G=(V, E)` and a positive weight function `w(v)` on vertices, find a vertex cover `V' subseteq V`, such that `w(V') = sum_(v in V') w(v)` is as small as possible.
• Our vertex cover algorithm from before treats all vertices equally and may return a very heavy cover, so a new algorithm is needed for this problem.
• We are going to give a linear programming-based algorithm to get a solution.

0-1 Program for Minimum Weight Vertex Cover

• In a linear program, we are trying to maximize or minimize a function of several variables, subject to a set of linear inequalities on those variables.
• In our case, to each vertex `v in V` associate a 0 or 1 valued variable `x(v)`. We put `v` in the vertex cover iff `x(v)=1`.
• The constraint that for any edge `(u,v)` one of `u` or `v` must be in the vertex cover, can be represented as the constraint `x(u) + x(v) ge 1`.
• This gives us the following 0-1 integer program for minimum weight vertex cover:
  minimize
  `sum_(v in V) w(v) x(v)`
  subject to
  `x(u) + x(v) ge 1` for each `(u,v) in E`
  `x(v) in {0, 1}` for each `v in V`.
• The special case where all the `w(v)` are 1 is the optimization version of the NP-hard vertex cover problem, so the above kinds of programs are hard to solve.

Using Relaxation to Approximately Solve Problems

• If instead of requiring `x(v) in {0,1}`, we only require `0 le x(v) le 1`, we obtain the following linear program:
  minimize
  `sum_(v in V) w(v) x(v)`
  subject to
  `x(u) + x(v) ge 1` for each `(u,v) in E`
  `x(v) le 1` for each `v in V`.
  `0 le x(v)` for each `v in V`.
• This is known as the linear programming relaxation of our 0-1 program.
• Notice any feasible solution (a setting to the variables that satisfies all the constraints) to the original 0-1 integer program is also a feasible solution to the linear program.
• So an optimal solution to the linear program gives a lower bound on the value of an optimal solution to the 0-1 integer program, and hence a lower bound on the optimal weight in the minimum weight vertex-cover problem.

Approximation Algorithm For Minimum Weight Vertex Cover

• We now use the linear program from the last slide together with rounding to get an approximation algorithm for minimum weight vertex-cover.

APPROX-MIN-WEIGHT-VC(G, w)
1 C = ∅
2 Compute x, an optimal solution to the 
  linear program of the previous slide
3 for each v ∈ V
4     if x(v) ≥ 1/2
5         C = C ∪ {v}
6 return C

• One can use the ellipsoid method to find an optimal solution to the linear program in `p`-time (`n^4L`, where `L` is the number of digits) (see Chapter 29 of the book). We will assume, we are just calling some software package that implements this.

APPROX-MIN-WEIGHT-VC is a 2-approximation algorithm

Theorem. APPROX-MIN-WEIGHT-VC is a polynomial time 2-approximation algorithm for the minimum-weight vertex-cover problem.

Proof. As we have already mentioned, line 2 in the algorithm can be done in p-time using the ellipsoid method. Lines 3-5 are linear time in the number of vertices, so the whole algorithm is p-time.

Let `C^star` be an optimal solution to a minimum-weight vertex-cover problem. Let `z^{\star}` be an optimal solution to the linear program described on the previous slides. Since an optimal cover is a feasible solution to the linear program, we have
`z^{\star} le w(C^star)`.
The Theorem follows from the following claim which we prove on the next slide:

Claim. The rounding of variables `x(v)` in APPROX-MIN-WEIGHT-VC produces a set `C` that is a vertex cover and satisfies `w(C) le 2z^{\star}`.

Proof of Claim

As one of our constraints is `x(u) + x(v) ge 1`, at least one `x(u)` or `x(v)` must be at least 1/2. Therefore, at least one of `u` or `v` is included in the vertex cover, and so every edge is covered.

Consider the weight of the cover. We have
`z^{\star} = sum_(v in V) w(v) x(v)`
`ge sum_(v in V; x(v) ge 1/2)w(v) x(v)`
`ge sum_(v in V; x(v) ge 1/2)w(v) 1/2`
`= sum_(v in C)w(v) 1/2`
`= 1/2 sum_(v in C)w(v)`
`= 1/2 w(C)`
So this gives:
`w(C) le 2z^{\star} le 2w( C^star)`
completing the proof.

The Optimization Version of Subset Sum

• In subset sum we are given a pair `(S,t)` where `S` is a set of positive integers `{x_1, ..., x_n}` and `t` is a positive integer and the goal is to find a subset of `S` which sums to `t`.
• We showed this problem was `NP`-complete last week.
• In the optimization problem, we wish to find a subset of `S` whose sum is a large as possible but is still `le t`.
• For example, we may have a ship that when loaded with more than `t` tonnes of goods will sink.
• We can imagine having `n` containers `{1, ..., n}` that need to be shipped such that container `i` have weight `x_i`.
• If we get paid by the tonne, we want to load as much as possible on the ship without sinking it.

An Exponential-time Exact Algorithm

• One way to solve the previous task is the following:

  bestS' = ∅
  bestW = 0
  foreach S' ⊆ S:
     w := ∑x ∈ S'x
     if w > bestW and w ≤ t:
          bestW := w
          bestS' := S'
  return bestS'
  

• As there are `2^(|S|)` subsets we would have to cycle over, this is an exponential time algorithm.
• We can do a little better than the above... namely, when computing the sum, if it ever exceeds `t`, we can skip to the next subset.
• We can thus modify the algorithm so that it iteratively computes `L_i`, the list of sums of all subsets of `{x_1, ..., x_i}` that do not exceed `t`, and then return the maximum value of `L_n`.

Improving the Exponential Time Algorithm

• If `L` is a list of positive integers and `x` is another positive integer, let `L +x` denote the list of positive integers obtained by increasing each element of `L` by `x`.
• So if `L = langle 1,2,3,5,9 rangle` then `L + 2 = langle 3, 4, 5, 7,11 rangle`.
• We use a similar notation for sets rather than lists:
  `S + x = {s +x | s in S}`.
• Suppose `L` and `L'` are sorted lists, let MERGE-LISTS(L, L') be the procedure which uses two counters to scan through the elements of `L` and `L'` once and outputs the sorted list with all the elements of each of these lists and with duplicates removed. As this is just one scan of the two lists, its runtime is `O(|L| + |L'|)`.
• Using this, our improved procedure for exact subset sum is:

  EXACT-SUBSET-SUM(S, t)
  Here S = {x[1], ... x[n]}
  1 n = |S|
  2 L[0] = (0)
  3 for i = 1 to n
  4     L[i] = MERGE-LISTS(L[i-1], L[i-1] + x[i])
  5     remove from L[i] every element that is greater than t
  6 return the largest element in L[n]
  

Example of Exponential Time Algorithm

• Let `P_i` denote the set of all values obtained by selecting a subset of `{x_1, ..., x_i}` and summing its members.
• For example, if `S = {1, 4, 5}`, then
  `P_1 = {0, 1}`
  `P_2 = {0, 1, 4, 5}`
  `P_3 = {0, 1, 4, 5, 6, 9, 10}`.
• Given the identity
  `P_i = P_(i-1) cup (P_(i-1) + x_i)`,
  by induction on `i`, we have that the list `L_i` is a sorted list containing every element of `P_i` whose value is not more than `t`.
• Unfortunately, the length of `L_i` can be as much as `2^i`, so this is an exponential time algorithm.
• If, however, `t` is polynomial in `|S|`, or if all the numbers in `S` are bounded by a polynomial in `|S|` then this is a `p`-time algorithm.