Introduction

Recall a language `L` was a set of strings over an alphabet, `A`, and a decision procedure for `L` is a procedure, which when given a string `x` outputs "Yes", if `x in L`, and "NO", otherwise.
`NP` is the class of languages that have polynomial time verification algorithms. That is, there is a p-time algorithm `A(x,y)` and a polynomial `q` for each `L in NP` such that `x in L` iff `exists y \leq q(|x|)[A(x,y) = 1]`.
We have been studying the hardest languages in `NP`, the `NP`-complete languages (NPC). `L in NPC` if `L in NP`, and for any `L' in NP` then is a `p`-time function `f` such that `x in L'` iff `f(x) in L`.
Thousands of problems have been shown to be `NP` complete: scheduling problems, fault detection in circuits, program optimization, clustering, deadlock avoidance, minesweeper, etc.
In this class, we have shown so far CIRCUIT-SAT, SAT, 3-SAT, CLIQUE, VERTEX COVER, HAM-CYCLE are `NP`-complete.
We showed CIRCUIT-SAT was in `NPC` by directly showing how to reduce an arbitrary language in `NP` to CIRCUIT SAT.
For all the other results, we showed how to reduce a problem which we know is in `NPC` to the target language we are trying to show is in `NPC`.
For example, for HAM-CYCLE, the problem of whether there is some permutation of the vertices of a graph such that there is an edge between each adjacent vertex in the permutation and between the first and last vertex in the permutation, we showed how to take an instance `langle G, t rangle` of VERTEX COVER and map it to an at most polynomial bigger instance `G'` of HAM-CYCLE.
We replaced each vertex `u` in `G` with a collection of widgets `W_{uv}` one for each of its neighbors and we added `t` additional nodes `s_t`.
We then added edges so that if and only if there were `t` nodes `u_1`, ..., `u_t` in the original graph such that any node is adjacent to at least one of them, then there would be a path in `s_1` to `W_{u_1v_1^{(1)}` then through this to `W_{u_1v_1^{(2)}}`, ..., `W_{u_1v_1^{(k)}}`, then from here to `s_2`, `W_{u_2v_2^{(1)}` etc. forming a Hamiltonian cycle.
Today, we continue to show `NP`-completeness results.

Traveling Salesman Problem

In this problem a salesman must visit `n` cities. Between each pair of cities `{i, j}` there is a cost `c_(ij)`.
We want to know if it is possible for the salesman to see each city exactly once (except twice for the start city) with cost less than `k`?
TSP = `{langle G, c, k rangle | G` is a complete graph, `c` is the cost matrix, and `k` is an integer such that the traveling salesman has a tour of cost at most `k}`.

Theorem. TSP is `NP`-complete.

Proof. First given a tour we can verify if it satisfies the desired properties in polynomial time. So it is in `NP`. To see completeness we reduce HAM-CYCLE to it. Given an instance `G = langle V, E rangle` of Hamiltonian cycle, we build an instance of TSP as follows: We first let `G'` be the complete graph on the same vertices. Then we set `c_(ij) = 0` if `{i, j}` is in `E` and `c_(ij) = 1` otherwise. Then `langle G', c, 0 rangle` is in TSP iff `G` was in HAM-CYCLE.

SUBSET-SUM

In the subset-sum problem we are given a finite set `S subset NN` and a target `t in NN`. We then ask: Is there a subset `S' subseteq S` whose elements sum to `t`?
For example, if `S = {1,2,7, 14, 49}` and `t=16`, then the subset `S' = {2, 14}` is a solution.
Formally,
SUBSET-SUM = `{langle S, t rangle | exists S' subseteq S, t= sum_(s in S') s}`.
We assume in the framing of this problem that we are encoding the numbers in binary.

NP-Completeness of SUBSET-SUM

Theorem. SUBSET-SUM is `NP`-complete.

Proof. To see SUBSET-SUM is in `NP` notice if we are given an instance `langle S, t rangle` of subset sum and a particular encoding of set of integers `langle S' rangle`, by linear scan for each element of `S'` we can check if it is in `S`. Further, by another scan of `S'` we can compute the sum of the elements in `S'` and then check if they are equal to `t`. This whole procedure would take at most` O(|langle S, t rangle +langle S' rangle|^2)` and so is a polynomial time verification procedure for SUBSET-SUM.

To show SUBSET-SUM is `NP`-hard, i.e., any language in `NP` reduces to it, it suffices to reduce 3SAT to SUBSET-SUM, as we already showed 3SAT is `NP`-complete. Suppose `phi(x_1, ..., x_n)` is an instance of 3SAT with clauses `C_1, ..., C_k`. WLOG, we can assume each clause has exactly three distinct literal, no clause has both a literal and its negation, and each variable appears in at least one clause.

The reduction creates two numbers in set `S` for each `x_i` and two numbers in `S` for each `C_j`. Numbers will be created in base 10, where each number contains `n + k` digits and each digit corresponds to either one variable or one clause. Proof continues next slide...

NP-Completeness of SUBSET-SUM cont'd

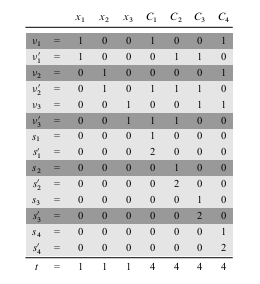
As we can see from the above picture we construct `S` and `t` by labeling each digit position by either a variable or a clause. The least significant `k` digits are labeled by clauses, and the most significant `n` digits are labeled by variables. In the picture above `phi = C_1 ^^ C_2 ^^ C_3 ^^ C_4`, where `C_1 = (x_1 vv neg x_2 vv neg x_3)`, `C_2 = (neg x_1 vv neg x_2 vv neg x_3)`, `C_3 = (neg x_1 vv neg x_2 vv x_3)`, and `C_4 = (x_1 vv x_2 vv x_3)`.

The target `t` has a `1` in each digit labeled by a variable and a `4` in each digit labeled by a clause.
For each variable `x_i`, there are two integers `v_i` and `v'_i` in `S`. Each has a `1` in the digit labeled by `x_i` and `0`'s in the other variable digits. If literal `x_i` appears in clause `C_j`, then the digit labeled by `C_j` in `v_i` contains a `1`. If literal `neg x_i` appears in clause `C_j`, then the digit labeled by `C_j` in `v'_i` contains a `1`. All other digits are labeled `0`.
For each clause `C_j`, there are two integers `s_j` and `s'_j` in `S`, Each has `0`'s in all digits other than the one labeled by `C_j`. For `s_j`, there is a `1` in the `C_j` digit, and `s'_j` has a `2` in this digit.

NP-Completeness of SUBSET-SUM Cont'd Some More

The maximum sum of digits in any digit position is at most `6`, so we don't have to worry about carries when we add numbers in `S`. `S` contains `2n + 2k` values each with `n +k` digits, where the time to produce a digit is polynomial in `n+k`, each digit of the target can be computed in constant time, so the whole reduction from `phi` to the `S` described above is `p`-time.

Suppose `phi` is satisfiable. If `x_i = 1` in this assignment include `v_i` in `S'`; otherwise include `v'_i` in `S'`. The sum of the `x_i` digit positions in `S'` will be `1` as we are only including one of the two `v_i`'s and all other `v_j`'s have `0` in the `x_i` digit position.

If we sum a `C_j` digit position from the elements so far added to `S'` we would get either `1`, `2`, or `3` depending on how many variables in the assignment satisfy this clauses. We can then add either `s_j` or `s'_j` or both to `S'` to ensure we get a sum of `4`. Hence, we have shown there exists an `S'` which achieves the target.

Suppose we have have constructed `S` and `t` as above, and there is an `S'` that achieves the target sum. Then to satisfy the `x_i` digit columns we must have exactly one of `v_i` or `v'_i` in `S'`. From which we can get an assignment for `phi`. The fact that the `C_j` column sum targets were achieved will ensure this is a satisfying assignment.

Quiz

Which of the following statements is true?

There exist `NP`-hard languages which are not in `P`.
We showed in class CLIQUE is in `P`.
Our proof that HAM-CYCLE is NP-complete relied on the four-color theorem.

Approximation Algorithms, Performance Ratios

Since it seems hard to find exact solutions to the optimization problems associated with a given `NP`-complete problem, it is natural to ask if one can get approximate solutions in polynomial time?
We say an algorithm for a problem has an approximation ratio of `r(n)`, if for any input of size `n`, the cost `C` of the solution produced by the algorithm is within a factor of `r(n)` of the cost `C^star` of the optimal solution. That is, `max(C/C^star, C^star/C) le r(n)`.
We call an algorithm that achieves an `r(n)`-approximation ratio an `r(n)`-approximation algorithm.
Some `NP`-complete problems have a trade-off between the approximation ratio and the run time.
An approximation scheme for an optimization problem is an algorithm that takes both an instance of the problem as well as a constant `epsilon` and then runs a `(1 + epsilon)`-approximation on the instance.
If for any `epsilon`, the approximation scheme run in `p`-time, then it is called a polynomial time approximation scheme.
We say that an approximation scheme is a fully `p`-time approximation scheme if it is an approximation scheme and its run time is `p`-time in both `1/epsilon` and the instance size `n`. For example, the scheme might have a running time of `O((1/epsilon)^2n^3)`.

The Vertex Cover Problem

The optimization problem associated with VERTEX-COVER is to find the least vertex cover of a instance graph `G`.
The following algorithm takes a graph `G` and outputs a vertex cover within twice the optimal.

APPROX-VERTEX-COVER(G)
1 C=∅
2 E'= E[G]
3 while E' ≠ ∅
4    let {u, v} be an arbitrary edge of E'
5    C = C ∪ {u, v}
6    Remove from E' every edge incident with either u or v
7 return C.

Analysis of APPROX-VERTEX-COVER

Theorem. APPROX-VERTEX-COVER is a p-time 2-approximation algorithm.

Proof. First, the algorithm runs in time `O(|V| +|E|)`, as we delete two vertices and at least one edge each time through the loop.

The set `C` returned by the algorithm is a vertex cover, since each edge that is removed is covered by some vertex in `C`. And the loop continues till no edges left.

To see that the cover returned is at most twice the optimal, let `A` denote the set of edges which were picked in line 4. In order to cover the edges in `A`, any vertex cover (including the optimal `C^star`) must include at least one endpoint of each edge in `A`. No two edges in `A` share an endpoint, so no two edge from `A` are covered by the same vertex from `C^star`. So `|C^star | ge |A|`. On the other hand `|C| = 2|A|`.

Approximating the Traveling Salesman Problem

The optimization problem associated with TSP is to find a tour of least cost.
Here is a 2-approximation algorithm for this problem when the triangle inequality holds on the distances between cities.

APPROX-TSP-TOUR(G, c)
1. Select a vertex r to be a root vertex
2. Compute the minimal spanning tree for G from root r using Prim's algorithm
3. Let L be the list of vertices visited in a pre-order tree walk of T
4. return the Hamiltonian cycle H that visits the vertices in order L.

Subroutines used by our algorithm

Recall in a pre-order traversal of a graph starting from some node, we visit each child we have not yet visited, and then visit the current node.
Recall Prims algorithm contructs a minimal spanning tree from a tree so far, denoted `A`, which at the start of the algorithm is the empty tree.
We maintain a priority queue of all the vertices not in A.
The priority, `v.key`, for a vertex `v` in the queue is the least weight of any edge connecting `v` with `A`. If no such edge exists than it is `infty`.
Let `v.pi` be the parent of `v` in the tree. Rather than explicitly have an `A` we use this parent structure to get the tree when the algorithm terminates.

Here is the pseudo-code:

MST-PRIM(G, w, r) // r is a starting node to grow the tree from
01 for each u in G.V
02    u.key = infty
03    u.pi = NIL
04 r.key = 0
05 r.pi = 0;
06 Q = MAKE-QUEUE(G.V) //will have all vertices
07 while Q != 0
08     u = EXTRACT-MIN(Q)
09     for each v in G.adj[u]
10        if v in Q  and u.key + w(u, v) < v.key
11            v.pi = u
12            v.key = u.key + w(u,v) //call appropriate DECREASE-KEY

Analysis of APPROX-TSP-TOUR

Theorem. APPROX-TSP-TOUR is a p-time 2-approximation algorithm for TSP with triangle-inequality holding on the cost function.

Proof. The minimal spanning tree algorithm runs in time `O(|V|^2)`. The remaining step take at most `O(|G|)` time.

Let `H^star` denote the optimal tour of the vertices. Since we can obtain a spanning tree from any tour by deleting an edge, we have `c(T) le c(H^star)` where `T` is our minimal spanning tree. A full walk `F` of `T` lists the vertices when they are first visited and also whenever they are returned to after a visit to a subtree. So `c(F) = 2c(T) le 2c(H^star)`. A full walk is typically not a tour since it lists some vertices twice.

On the other, the `H` returned by the algorithm is a tour and satisfies `c(H) le c(F)`, since it is obtained by deleting vertices from the full walk and since the triangle inequality holds. We are using the triangle inequality as if we have a sequence `a b c` in the full walk and delete `b`, our tour we want that the cost does not rise.

TSP and SUBSET-SUM are NPC, Approximation Algorithms

Outline