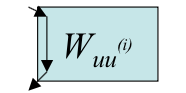Outline
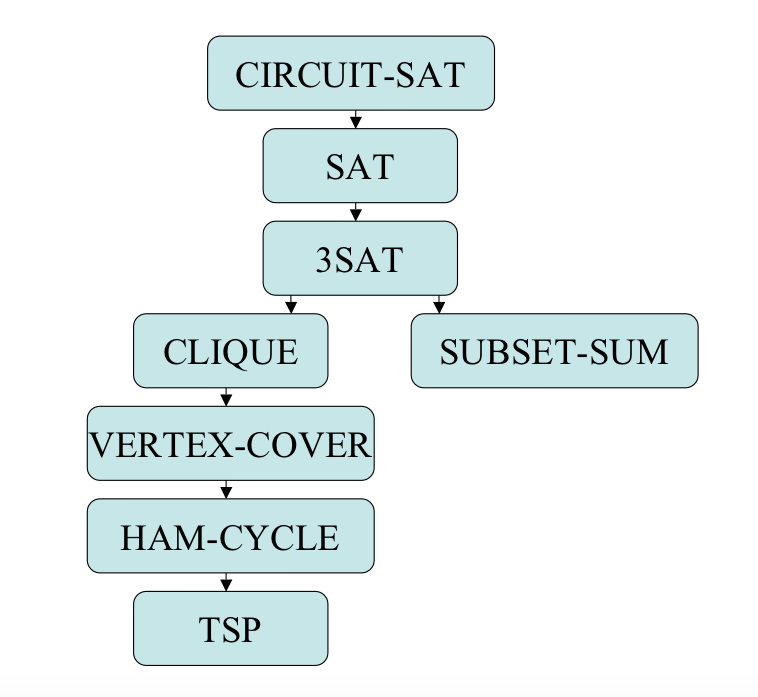
- NP-completeness Reductions We Will Show
- CLIQUE
- VERTEX-COVER
- In-Class Exercise
- HAM-CYCLE
- TSP
- SUBSET-SUM
Introduction
- On Monday, we were talking about
the classes `P` and `NP` and about `NP`-completeness.
- We said a language was in `P` if it has a polynomial time decision procedure (i.e., an algorithm
that runs in `p`-time in its input size that outputs "yes" if in language and "no" if not).
- We said a language `L` was in `NP` if there is a polynomial time verification algorithm `A(x,y)` and a polynomial
`q` such that `x in L` iff there exists `y` such that `|y| leq q(|x|)` and `A(x,y)` outputs 1.
- We said a language `L` is `p`-time reducible to another language `L'`, written `L leq_p L'`, if there
is a polynomial time computable map `f` from strings to string such that `x in L` iff `f(x) in L'`.
- A language `L` is said to be `NP`-complete if it is in `NP` and any other language in `NP` is `p`-time reducible
to `L`.
- We have shown several problems related to satisfiability to be `NP`-complete: CIRCUIT-SAT, SAT, 3SAT.
- Today, we exhibit several more `NP`-complete languages: CLIQUE, VERTEX-COVER, HAM-CYCLE, TSP,
SUBSET-SUM, the last of which will serve as a starting point for approximation algorithms.
Reductions We Will Show
CLIQUE
- A clique in an undirected graph `G=(V, E)` is a subset
`V' subseteq V` of vertices in which each pair of vertices from `V'` is connected by an edge.
- CLIQUE = `{langle G, k rangle | G ` is a graph with a clique of size `k}`.
Theorem. CLIQUE is `NP`-complete.
Proof. First CLIQUE is in `NP` because we can just guess a set of more
than `k` vertices and check for each possible edge between these vertices. Next we show how to
reduce 3SAT to CLIQUE. Let
`F = C_1^^C_2... ^^ C_k`
be an instance of 3SAT. For each `C_r= (l_1^r vv l_2^r vv l_3^r )`, we put a
triple of vertices into our graph `G`, `v_1^r, v_2^r, v_3^r`. We put an edge
between vertices `v_i^r` and `v_j^s` if they are in different triples
and their corresponding literals are not negations of each other.
Let `(G, k)` be the output instance of CLIQUE. Notice if there is a
satisfying assignment to `F` then if we look at the corresponding
vertices `v_j^r` of at least one satisfied literal/clause, it will
be a CLIQUE of size `k` in `G`. As there are no edges between vertices
coming from the same clause, any CLIQUE of size `k` has to have at
least one vertex `v_j^r` for each `1 le r le k`. Choosing an assignment so
that the corresponding literals for each `v_j^r` evaluates to true gives
a satisfying assignment. So the reduction works.
CLIQUE Example
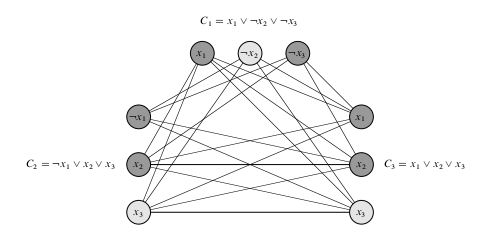
- Suppose we had the 3SAT instance `phi = C_1 ^^ C_2 ^^ C_3` where
`C_1 = (x_1 vv neg x_2 vv neg x_3)`, `C_2 = ( neg x_1 vv x_2 vv x_3)`, and `C_3 = (x_1 vv x_2 vv x_3)`
- Given this formula, the reduction from the previous slide would compute the
graph above.
- Notice if we set `x_2` to false and `x_3` true, the original formula is made true regardless of
the value of `x_1`.
- This corresponds to the clique of size 3 given by the white vertices in the above.
- Consider the assignment which sets all of the variables false. This makes the formula false.
In this case, there is no edge from `neg x_2` to `neg x_3` so it is not a clique.
VERTEX-COVER
- A vertex cover in an undirected graph `G=langle V, E rangle` is a
subset of the vertices `V'` such that each edge in `G` is connected to a vertex in `V'`.
- VERTEX-COVER=`{langle G, k rangle` : graph `G` has a vertex cover of size `k}`
Theorem. VERTEX-COVER is `NP`-complete.
Proof. To see it is in `NP` notice if we guess a set of `k` edges
we can check if it is a vertex cover in polynomial time. To see it is `NP`-complete
we reduce CLIQUE to this problem. Let `bar(G)` denote the complement of a graph
`G= langle V, E rangle`, that is, the
graph with the same vertices, but with edges `{i, j}` iff `{i, j}` is not an
edge of `G`. Then notice `G` has a clique of size `k` iff `bar(G)` has a vertex
cover of size `|V| - k`.
In-Class Exercise
- For each `n ≥ 1`, give an example graph on `n+1` vertices that has a vertex cover of size `1`.
- A `p`-time isomorphism is a `p`-time reduction which is one-to-one and onto and whose inverse is `p`-time computable. Argue the reduction of the last slide is an `p`-time isomorphism.
- What instances of CLIQUE would map to your graphs above?
- Post your solution to the Apr 24 In-Class Exercise Thread.
Hamiltonian Cycles
- Recall a Hamiltonian cycle is a permutation of the vertices
`v_(i_1),..., v_(i_n)` of a graph `G` so that there is an edge between
`{v_(i_j) , v_(i_j+1)}` for each `j` as well an edge `{v_(i_n) , v_(i_1)}`.
- Let HAM-CYCLE be the language `{langle G rangle | G` contains a Hamiltonian cycle`}`.
Theorem. HAM-CYCLE is `NP`-complete.
Proof. First, given a permutation of the vertices, we can in
polynomial time verify whether or not it is a Hamiltonian cycle. So HAM-CYCLE is in `NP`.
To see it is `NP`-complete, we show VERTEX-COVER `le_p` HAM-CYCLE. Given a graph `G` and
an integer `k`, we need to make a new graph `G'` which has a Hamiltonian cycle iff
the original had a vertex cover of size `k`...
More NP-Completeness Proof of HAM-CYCLE
We will make use of the following widget `W_(uv)` to build a new graph `G'` from `G`:
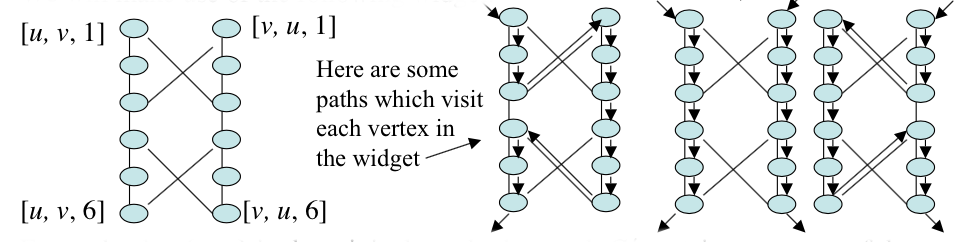
The middle path in our example paths above will be used if `u` and `v` are both in cover of `G`.
For each edge `{u, v}` in the original graph, the graph `G'` contains one copy of the widget
`W_(uv)` (i.e, `W_(uv)` and `W_(vu)` are the same widget) and we denote the edges of the widget by
`[u, v, i]` or `[v, u, i]` according to if they are on the left or right side. Only the tops and
bottoms of widgets will be connected to the rest of the graph `G'`. In our construction, a
cycle must visit each widget, and there are exactly three different ways (as shown above) one could
visit all the vertices of the widget: start on the left side, the right side, or do the two sides
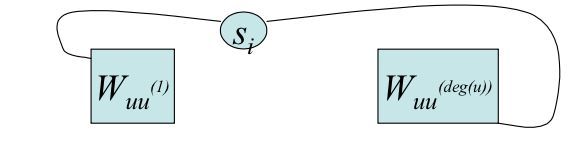
separately. In addition to the vertices of the widgets, we will have selector vertices,
`s_1,..., s_k`. The edges chosen in these selector vertices will correspond to the `k` vertices of the
vertex cover in `G`. We also have two additional types of edges besides those in the widgets that
we describe on the next slide.
Connecting Widgets and Selector Vertices/Edges
- For each `u in V` of `G`, let `u^{(i)}` denote the vertices connected to `u` by an edge in `G`.
To `G'`, we add edges to form a path containing all widgets
corresponding to edges `{u, u^((i))}`. To do this we add the edges:
`{{[``u, u^((i)), 6``], [``u, u^((i+1)), 1``]``} | u in V}`
to `G'`. So we can construct a path from `[u, u^((1)), 1]` to `[u, u^((deg(u))), 6]` using
these additional edges.
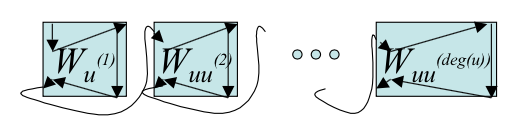
If both `u` and `u^((i))` are in a vertex cover of `G` then we traverse a widget as
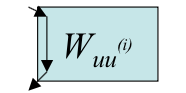
- The second kind of additional edges are of the form
`{\{s_i,[u,u^((1)) ,1]\} | u` is in `V` and `1 le i le k} cup`
`qquad {\{s_i, [u,u^((deg(u))) ,6]\} | u` is in `V` and `1 le i le k }`.
Conclusion HAM-CYCLE is NP-Complete
- If `G= langle V, E rangle` then notice the size of a widget is constant and we have `|E|` widgets.
- We also have only k selector vertices.
- Of the additional edges described on the previous slide, there are at most sum of the degrees vertices of the first type.
- There are at most `2k|V|` additional edges of the second type.
- So in all the new graph `G'` will be polynomial size in `G`.
- Suppose `G` has a vertex cover `{u_1,.. u_k}`. A Hamiltonian cycle in `G'`
can be obtained by starting at `i=1` and for each `i` thereafter follow
`s_i` to `[u_i, u_i^((1)),1]` and then the path from the previous slide to `[u_i, u_i^((deg(u_i))),6]`.
Then from there one can follow the edge `{s_(i+1), [u_i, u_i^((deg(u_i))), 6]}`. Finally,
one can following the edge `{s_k, [u_k, u_k^((deg(u_k))), 6]}` back to the start.
- Since each edge in `G` is incident with one vertex in the vertex cover each
widget will have all of its vertices hit by this path if there is cover.
- On the other hand, if there is a Hamiltonian cycle in `G'` then
`V^(star) ={ u in V | {s_j, [ u, u^((1)), 1]}` is in the cycle for some `1 le j le k}`
will be a vertex cover of size `k` in `G`.
HAM-CYCLE Reduction Example
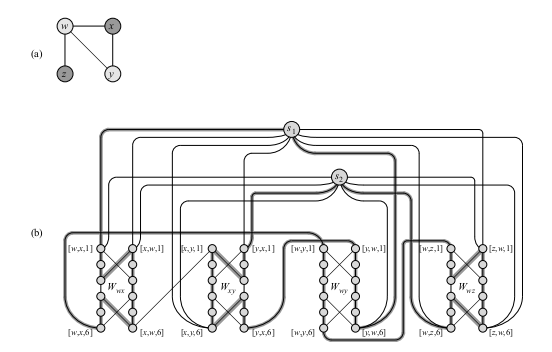
- Give the instance of VERTEX-COVER of graph (a), our reduction will produce the graph (b) (some of the
edges to and from selector vertices have not been drawn).
- The fact that the lightly-shaded vertices in (a) correspond to a VERTEX is transformed to highlighted path
in (b) which is a Hamiltonian cycle.