Investment Strategies

An on-line trading application might represent a portfolio as an account with a list of investments. Adding a new investment to the portfolio involves decrementing the balance to provide funds for the new investment. An object representing the investment is then added to the portfolio's list. Of course how much money should be spent on the new investment depends on the investment strategy used. For example, a safe strategy might invest smaller amounts on high risk investments such as lottery tickets and larger amounts on low risk investments such as real estate and blue chip stocks.

Here's the static structure of our financial application:

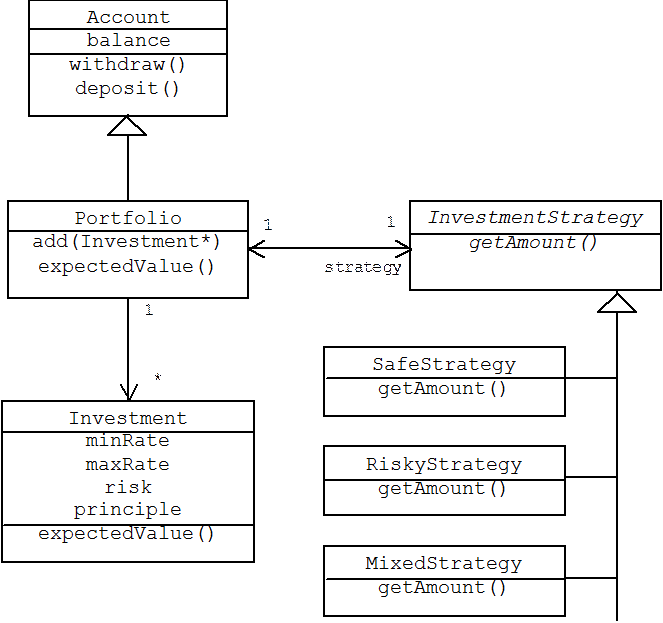
Four attributes describe an investment: the principle ( i.e., the amount initially invested); the maximum rate of return; the minimum rate of return (this is a number between -100% and the maximum rate of return); and the risk (this is a number between 0 and 1 indicating the probability of the lower rate of return). The expected value of an investment is simply the weighted sum of the maximum and minimum returns:

double Investment::expectedValue()
{
   double value =
      principle * (maxRate * (1 - risk) + minRate * risk);
   return value;
}

Of course the expected value of a portfolio is its balance plus the expected values of its investments:

double Portfolio::expectedValue()
{
   list<Investment>::iterator p;
   double value = getBalance();
   for(p = investments.begin(); p != investments.end(); p++)
      value += (*p).expectedValue();
   return value;
}

Before adding a new investment to a portfolio, the associated investment strategy is consulted to determine the amount that should be invested:

void Portfolio::add(Investment inv)
{
   double amt = strategy->getAmount(inv);
   if (0 < amt && amt <= getBalance())
   {
      inv.setPrinciple(amt);
      withdraw(amt);
      investments.push_back(inv);
   }
}

Of course the getAmount() function is a pure virtual function in the abstract InvestmentStrategy base class:

class InvestmentStrategy
{
public:
   virtual double getAmount(Investment inv) = 0;
   void setPortfolio(Portfolio* p) { pf = p; }
protected:
   Portfolio* pf;
};

The actual implementation is specified in derived classes, and of course one derived class might implement this function quite differently from another.

For example, suppose a client defines the following investments. (The Investment constructor arguments specify the maximum rate of return, minimum rate of return, and risk, respectively. The principle is initially $0.)

Investment  lotteryTicket(50000, -1, .99999),
            bond(1.2, 1.1, .1),
            hiTechStock(4, -.5, .6),
            blueChipStock(1.5, 0, .6),
            junkBond(2, -1, .4),
            realEstate(2, -.1, .2);

Next, two portfolios are created, one that uses a safe investment strategy, another that uses a risky strategy:

Portfolio p1(1000, new SafeStrategy());
Portfolio p2(1000, new RiskyStrategy());

Copies of the same investments are added to each portfolio:

p1.add(lotteryTicket);
p1.add(hiTechStock);
p1.add(blueChipStock);
p1.add(junkBond);
p1.add(realEstate);

p2.add(lotteryTicket);
p2.add(hiTechStock);
p2.add(blueChipStock);
p2.add(junkBond);
p2.add(realEstate);

However, the expected value of p1 is larger than the expected value of p2. This difference arises because p2 invested heavily in lottery tickets, junk bonds, and high-tech stocks according to its risky strategy, while p1 invested more heavily in  real estate and blue chip stocks according to its safe strategy. (Of course the actual values of the portfolios will depend on fate, karma, and luck.)