Partonomy
Classifying Part-Whole Relationships
An important category of relationships (i.e., associations) have the form:
Object X is part of object Y
For example:
Engine X is part of car Y
These are called part-whole, meronymic, or partonomic relationships.
Philosophers classify part-whole relationships according to how they combine the following three properties:
C = configurational = parts have a functional/structural relationship to each other or whole
H = homogeneous = parts same kind as whole
I = invariance = parts can't be separated from the whole
For example, a
sub-category of partonomic relationships are those that are configurational,
non-homogeneous, and non-invariant (CHI). Thus, there is a total of
eight possible categories of patonomic relationships. Six are common, and two
are represented in UML.
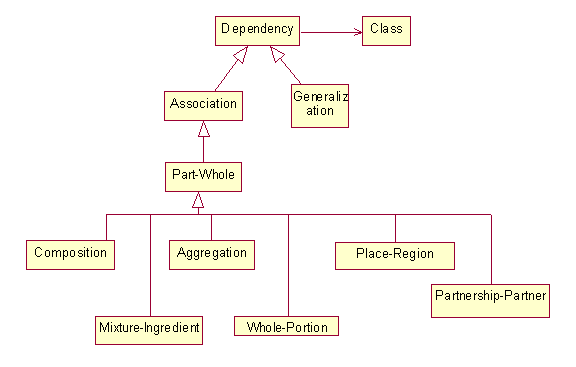
Composition or Assembly/Component Aggregation (CHI)
An engine is part of a car.
A piston is part of an engine.
Aggregation or Container/Member Aggregation (CHI)
A car is part of a fleet of cars.
Other types of part-whole relationships
Mixture/Ingredient Aggregation (CHI)
Flour is a part of a loaf of bread.
Metal is part of a car.
Whole/Portion Aggregation (CHI)
A slice of bread is part of a loaf of bread.
Place/Region Aggregation (CHI)
Partnership/Partner (CHI)
Part-Whole Relationships in UML
We can represent the categories of Part-Whole relationships using a UML class diagram:
Transitivity Problem
Assume we represent the relationship X is part of Y by:
X is part of Y
Assume:
X is part of Y and Y is part of Z
Can we infer:
X is part of Z
In other words, is the is part of relationship transitive?
Generally, transitivity fails unless both is part of relationships have the same CHI type as defined above.
For example, the first inference is valid, but not the second:
piston part of engine
engine part of car
piston part of car
engine part of car
car part of fleet
engine part of fleet
Non Part-Whole Relationships
Topological Inclusion
the customer is in the store
Classification Inclusion (is-a)
"Moby Dick" is a book
Attribution
Smith is 5 feet tall
Attachment
Feet are attached to legs
Ownership
Smith owns a bicycle
The Composite Design Pattern
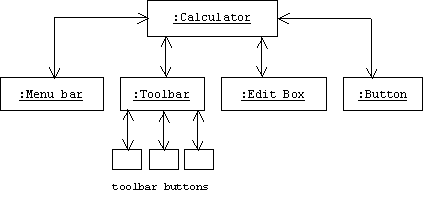
A calculator is an example of a composite object. We can treat it as an individual object that encapsulates its components: the menu bar, toolbar, buttons, labels, and boxes, or, when it's convenient, we can ignore the calculator and treat its components as individual objects.
Of course some of the calculator's components are also composites. For example, the toolbar is a composite consisting of several buttons. Sometimes it's convenient to think of a calculator as a tree-like structure:
Composites are so common, that they are included in many pattern catalogs:
Reference
James Odell; Six Different Kinds of Composition; Journal of Object-Oriented Programming Vol 5, No 8. January 1994.