Language Processors

The two types of language processors we are interested in: interpreters and compilers.

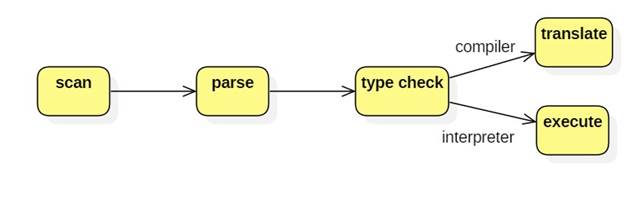
Typically, programmers interact with an interpreter through a console window running a REPL (read-execute-print loop). The programmer enters an expression and the interpreter prints the value:

-> 2 + 3 * 4
14
-> "bat" + "man"
"batman"
-> square(10)
100
->

A compiler reads a program from one or more files, then translates the program into one or more files of assembly language instructions for a particular hardware platform. The assembly language files can be linked and assembled into an executable file of machine language instructions:

load reg[0], 3
load reg[1], 4
mul reg[2], reg[0], reg[1]
load reg[0], 2
add reg[3], reg[0], reg[2]

Notes

·       An assembler is a translator that translates assembly language programs to machine language programs.

·       A cross-compiler translates one high-level language into another. For example: C++ to Java.

·       A de-compiler translates assembly language into a high-level language. This might be useful if the source code of a program was lost.

Scanning

·       Initially an expression/program is just a string.

·       A scanner converts the string into a sequence of tokens.

·       Examples of tokens include: numbers, identifiers (i.e., names), punctuation marks, and operator symbols.

token ::= number | identifier | operator | punctuation | etc.

·       Of course, the scanner throws a syntax exception if an illegal token is encountered.

·       Example:

scan("3 + 2 * 53") = ["3", "+", "2", "*", "53"]

·       The set of all legal tokens is defined by a regular expression. For example:

o   A number is one or more digits optionally followed by a decimal point followed by one or more digits:

         number ::= [0-9]+("."[0-9]+)?

Parsing

·       A parser uses a formal grammar to transform an input expression from a list of tokens into a tree (unless a syntax error is detected).

·       The tree tells the execution module in which order the sub-expressions should be executed.

·       For example, here's a formal grammar for a simple language called SOP (Sums of Products):

o   A sum is one or more products separated by plus signs:

     sum ::= product ~ ("+" ~ product)*

o   A product is one or more terms separated by multiply signs:

     product ::= term ~ ("*" ~ term)*

o   A term is a number or a sum in parentheses:

     term ::= number | "(" ~ sum ~ ")"

o   A number is an optional sign followed by one or more digits:

     number ::= ("+" | "-")? ~ [0-9]+

Parsing "2 * 3 + 5" using the SOP grammar:

parse("2 * 3 + 5", SOP)

produces the tree:

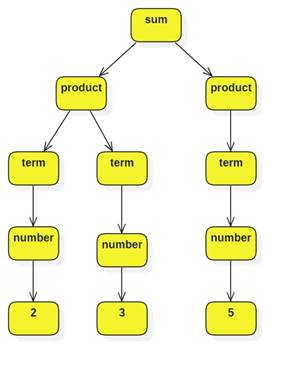
We can represent this as a Lisp-like expression (+ (* 2 3) 5)

Execution

·       Execution uses an environment to transform an expression in the form of a tree into a value.

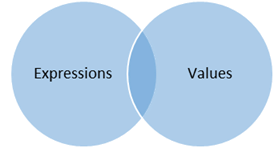
·       The Expression-Value Dichotomy is one of the most important distinctions in programming languages. It is the distinction between expressions (programmer input) and values (computer output). The intersection of these two domains are literals: expressions that are also values, like numbers, Booleans, and characters.

                                           

·       For now, we can think of an environment as a symbol table that associates names to values:

·       For example:

execute(parse(scan("x * pi + z"), SOP?), env) = execute((+ (* x pi) z), env) = 319.0

Terminology

·       Syntax refers to the grammatic structure of an expression, while semantics refers to the behavior of an expression when it is executed.

·       Meta-language refers to the implementation language of a language processor, while the language being processed is called the object language.

Type Checking

·       Like parsing, type checking uses rules such as:

o   f(x) has type B if x has type A and f is a function with domain A and range B

      f(x): B :- x: A, f: A=>B                              

o   x has type B if x has type A and A is a subtype of B

      x: B :- x: A, A <: B

·       For example:

sin(PI): Double because PI: Double and sin: Double => Double

"hello": Object because "hello": String and String extends Object

not(3): Error because not: Boolean => Boolean, but 3: Integer

Translation

A translator translates an expression into an equivalent sequence of assembly language instructions.

For example, the assignment statement:

x = 3 + 2 * 5

might be translated to the sequence:

load reg[0], 5
load reg[1], 2
mul reg[2], reg[0], reg[1]
load reg[0], 3
add reg[3], reg[0], reg[2]
store reg[3], x

Notes:

·       Of course different types of processors have different assembly languages, so a programming language might need many translators.

Formal Specification

·       Formal Specification of Programming Languages