Top-Down Design

The basic idea behind procedural programming is top down design: when main() gets too long—say more than half a page –we break it up into calls to loosely coupled, coherent supporting functions. We apply the same idea to the supporting functions. We repeat this process until there are no more supporting functions to be defined.

Example: Computing Volumes of Capped Pipes

Assume a plumbing supply manufacturer assembles pipes capped at both ends:

The assemblies have different lengths (l) and diameters (d). The manufacturer would like a program able to execute the commands:

vol DIAM LEN
area DIAM LEN

where

DIAM = d = the pipe's diameter
LEN = l = the pipe's length

Let's reuse our control loop. This means we must implement an appropriate execute function. This function will fetch the diameter and length, then, depending on the command, compute the desired result:

double execute(string cmmd)
{
double diam, len;
cin >> diam >> len; // fetch dimensions
if (diam <= 0 || len <= 0)
{
cerr << "Error: dimensions must be positive\n";
return 0;
}
if (len <= diam)
{
cerr << "Error: length must be larger than diameter\n";
return 0;
}
if (cmmd == "vol") return pipeVolume(len, diam);
else if (cmmd == "area") return pipeArea(len, diam);
else
{
cerr << "Error: unrecognized command: " << cmmd << endl;
cin.sync(); // flush buffer
return 0;
}
}

Notice that we computed the volume of the pipe by calling a function named pipeVolume() and the area of the pipe by calling pipeArea.. Are these standard C++ library functions? It might be; it's worth a check, but alas, they are not. No worries, we'll define our own:

double pipeVolume(double l, double d)
{
return ???;
}

double pipeArea(double l, double d)
{
return ???;
}

Note that we can choose any names we want for our parameters, as long as there are two and they are of type double (because that's what the caller expects). Following the modularity principle, we look for some way to break pipeVolume() into calls to loosely coupled, coherent supporting functions. (pipeArea will be left as an exercise.) We use the physical geometry of the pipe as our guide. The pipe is assembled out of a cylinder of radius = d/2 and length = l – d and two hemispherical caps, which, when glued together, form a sphere of radius = d/2. The volume of our pipe is simply the sum of the cylinder volume and the sphere volume:

double pipeVolume(double l, double d)
{
return cylinderVolume(l - d, d/2) + sphereVolume(d/2);
}

Perhaps cylinderVolume() and sphereVolume() are standard C++ library functions. Again, it's worth checking, again we're disappointed, and again we must define our own:

double cylinderVolume(double len, double rad)
{
return ???;
}

double sphereVolume(double rad)
{
return ???;
}

The volume of a cylinder is the area of its circular base times its length:

double cylinderVolume(double len, double rad)
{
return len * circleArea(rad);
}

Is circleArea() in the C++ library? No, but the area of a circle is simply pi times the radius squared:

double circleArea(double rad)
{
return pi * square(rad);
}

Surely square() is in the standard library. Nope:

double square(double x) { return x * x; }

Pi must also be defined, but we will also need pi to compute the sphere's volume. If we define pi as a local variable of circleArea(), i.e. inside circleArea()'s block, then it won't be visible inside sphereVolume(). Even if we make pi a local variable of main() it won't be visible inside sphereVolume(). The solution is to make pi a global variable. A global variable is defined outside of all function blocks, including main()'s. the scope of a global variable is the entire program:

const double pi = acos(-1);

Of course sphereVolume() isn't in the C++ library, so we must define it. According to my geometry book the volume of a sphere is:

V = 4/3 pr³

It seems wasteful to recalculate the constant 4/3 p each time sphereVolume() is called. By defining it as a global variable it will be calculated once at the beginning of the program:

const double fourThirdsPi = pi*4.0/3.0; // warning: 4/3 = 1

Here is our implementation of sphereVolume():

double sphereVolume(double rad)
{
return fourThirdsPi * cube(rad);
}

What about cube()? It too must be defined:

double cube(double x) { return x * square(x); }

Now we can build (i.e. compile and link) and test our program:

type "quit" to quit
-> vol 5 20
359.974
-> vol 10 50
3665.19
-> vol 20 5
Error: length must be larger than diameter
0
-> vol -9 30
Error: dimensions must be positive
0
-> cost 12 34
Error: unrecognized command: cost
0
-> quit
bye
Press any key to continue

Here's a dependency graph for our application:

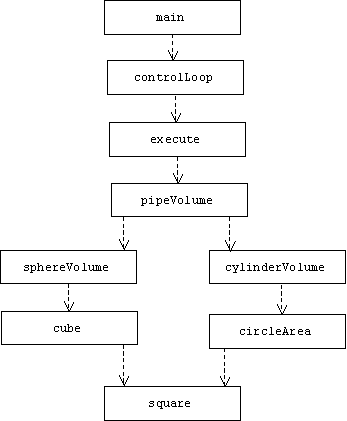
Note that we can eliminate the dependency of cube() on square() by redefining cube() as follows:

double cube(double x) { return x * x * x; }

This actually makes cube() more reusable because we only need to add cube() to a new project. We don't need to remember that square must also be added.

Here's an alternative implementation of pipeVolume(). It is correct, but would you want to maintain it?

double pipeVolume(double u, double k) { return u *
helper1(k) –
helper2(k)
+ helper3(k);} // Wally was right!

The three "helper" functions are not cohesive, hence not reusable:

double helper1(double x) { return 3.1416 * d * d / 4; }
double helper2(double x) { return d * helper1(d); }
double helper3(double x) { return helper2(d) * 2 / 3; }