Arrays and Pointers

Arrays

An array is a named group of several consecutive variables of the same type. Each of the component variables is accessed from the array name and an index number.

Assume SIZE is an integer constant:

const int SIZE = 3;

The following declaration creates three arrays, each consisting of three variables of type double:

double vec1[SIZE], vec2[SIZE], vec3[SIZE];

We can initialize these arrays using a for loop. Be careful, array indices start at 0, so the maximum valid index is SIZE – 1 = 2:

for(int i = 0; i < SIZE; i++)
{
vec1[i] = 2 * i + 1;
vec2[i] = i/2;
vec3[i] = 1;
}

Here is a picture of what's going on in the computer's memory:

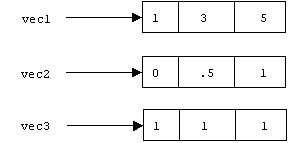
We can add the entries in vec1 to the corresponding entries in vec2 and store them in vec3 using a for loop:

for(int i = 0; i < SIZE; i++)
vec3[i] = vec1[i] + vec2[i];

Another for loop prints vec3:

for(int i = 0; i < SIZE; i++)
cout << vec3[i] << ' ';

Producing the output:

1 3.5 6

We can introduce Vector as an alternative name for length three arrays of doubles by using a typedef declaration, but the syntax is a little tricky:

typedef double VECTOR[SIZE];

Now we can simply declare vec1, vec2, and vec3 as VECTORs:

VECTOR vec1, vec2, vec3;

We can also initialize arrays in their declarations:

double vec4[3] = {100, 200, 300};

Of course we can also define arrays of arrays. This might be a good way to represent matrices:

double mat1[SIZE][SIZE], mat2[SIZE][SIZE];

We need a nested for loop to initialize these:

for(int i = 0; i < SIZE; i++)
for(int j = 0; j < SIZE; j++)
{
mat1[i][j] = 3 * i + j + 1;
mat2[i][j] = 2 * mat1[i][j];
}

Each row of one of our matrices is an ordinary array:

for(int i = 0; i < SIZE; i++)
vec3[i] = mat1[1][i] * mat2[i][1];

Pointers

Each variable has a unique address in the computer's memory. We can discover the address of a variable x using the address of operator: &x. For example, on my computer executing the statements:

int nums[3] = {100, 200, 300};

for(int i = 0; i < 3; i++)

cout << "&nums[" << i << "] = " << &nums[i] << '\n';

produces the output:

&nums[0] = 0012FF6C

&nums[1] = 0012FF70

&nums[2] = 0012FF74

Addresses, also called pointers, are usually given in hexadecimal notation. Notice that difference between two consecutive pointers is 4. That's because on my computer:

sizeof(int) = 4 (bytes)

If we change nums to an array of short ints, then the output produced is:

&nums[0] = 0012FF70

&nums[1] = 0012FF72

&nums[2] = 0012FF74

Differences between consecutive pointers is now 2 because on my computer:

sizeof(short) = 2 (bytes)

Although pointers look like integers, they are not. For example, it's illegal to store a pointer in an integer variable:

int x = 42;
int y = &x; // error

Instead, pointers must be stored in pointer variables. The type of all pointers to ints is called int*:

int x = 42;
int* y = &x; // ok

The syntax of a pointer declaration is a little tricky. Officially, a declaration has four parts:

SPECIFIER BASE_TYPE DECLARATOR INITIALIZER;

The specifier (e.g. const) and the initializer (e.g. = { 100, 200, 300 }) are optional. The base type is any valid C++ type name: int, float, vector<string>, etc. The declarator is a name and, optionally, some declarator operators. For example, recall the declaration of the nums array:

int nums[3] = {100, 200, 300};

This declaration has no specifier. The base type is int, the initializer is = {100, 200, 300} and the declarator consists of the name, nums, and the declarator operator [3]. The syntax is complicated because it suggests nums is an integer variable, but that's not the case.

As it turns out, even though * appeared next to the base type in:

int* y = &x;

It is also a declarator operator. C++ simply ignores the spaces. We could have written:

int *y = &x;

This can cause problems. For example, if we attempt to declare two pointers, we can get in trouble:

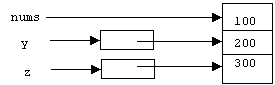
int* y = &nums[1], z = &nums[2]; // error: z is an int!

The correct syntax is:

int *y = &nums[1], *z = &nums[2]; // ok

Here's a picture representing the definitions we have at this point:

There's more confusion to come. What can we do with a pointer? Two things. We can dereference a pointer. This means we can discover the value stored inside the variable it points to. What's confusing is the syntax. We use the same operator used to declare the pointer type:

cout << *y; // prints 200
cout << *z; // prints 300

It's important to initialize pointers when they are declared. Otherwise, the pointer will contain some garbage value. Dereferencing a pointer containing a garbage value is the most common cause of programs crashing:

int *p; // forgot to initialize
cout << *p; // error, p doesn't point to anything

What if you don't have anything to initialize a pointer with at the point where it is declared? In this case initialize the pointer with 0, the null pointer:

int* p = 0;

Of course dereferencing the null pointer will also cause a program to crash, but at least we can check for the null pointer before dereferencing:

if (p) cout << *p; // ok

The other thing we can do is pointer arithmetic. For example:

cout << y << '\n'; // prints 0012FF70
y = y + 1;
cout << y << '\n'; // prints 0012FF74
cout << *y << '\n'; // prints 200

Notice, incrementing a pointer by 1 really increments it by sizeof(int).

Array Pointer Duality

There is a close relationship between pointers and arrays: arrays are constant pointers. C++ translates the expression:

nums[i];

into:

*(nums + i);

Here's another way to traverse an array. Note the similarity with iterators:

for(int* p = nums; p != nums + 3; p++)
*p = *p + 1;

Constant Pointers

Mixing the const specifier with pointer declarations creates four combinations. Assume the following declarations are made:

int x = 42;
int *a = &x;
const int *b = &x;
int const *c = &x;
const int const *d = &x;

Here is what you can and can't do with these pointers:

*a = 0; // ok
a++; // ok

*b = 0; // error, b points to a constant
b++; // ok

*c = 0; // ok
c++; // error, c is a constant

*d = 0; // error, d points to a constant
d++; // error, d is a constant

Heap Variables

The computer's memory is divided into four segments:

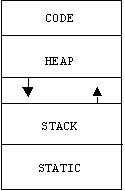
Local variables and parameters are allocated in the stack. Global variables are allocated in the static segment. Binary instructions are allocated in the code segment. The computer manages allocation and deallocation of variables in these segments, however, the programmer can allocate and deallocate variables in the heap segment while the program is running.

The new() operator allocates variables in the heap. It returns a pointer to the allocated variable:

int *p = new int(0);
double *q = new double(3.14);

The delete() operator deallocates heap variables so they can be reallocated later:

delete p;
delete q;

All of this would be pretty uninteresting if it weren't also possible to create array variables in the heap:

int* p = new int[50]; // p points to a heap array of length 50
for(int i = 0; i < 50; i++)
p[i] = i;

Use the delete[] operator to delete an array:

delete[] p;

A heap array is also called a dynamic array because, unlike ordinary arrays, they can be expanded. For example, to add one more element to p we can write:

int* temp = new int[100];
for(int i = 0; i < 50; i++)
temp[i] = p[i];
delete[] p;
p = temp;
p[50] = 50;

Examples

Example: Arrays as Parameters

An array-type variable declaration must declare the size of the array. This can be done using an array initializer or by placing a size inside the brackets:

int mt1[] = {78, 93, 45, 18, 88};
int mt2[10];

Of course in the second case the array must be filled using other means:

for(int i = 0; i < 10; i++)
mt2[i] = i * i;

An array-type parameter declaration never declares the size of the array. Instead, this is traditionally indicated by a second parameter:

double avg(int scores[], int size)
{
int total = 0;
for(int i = 0; i < size; i++)
total += scores[i];
return double(total)/double(size);
}

void print(int vals[], int size)
{
cout << "( ";
for(int i = 0; i < size; i++)
cout << vals[i] << ' ';
cout << ")";
}

Executing the following statements:

cout << "avg1 = " << avg(mt1, 5) << endl;
cout << "avg2 = " << avg(mt2, 10) << endl;

print(mt1, 5); cout << endl;
print(mt2, 10); cout << endl;

produces the following output:

avg1 = 64.4
avg2 = 28.5
( 78 93 45 18 88 )
( 0 1 4 9 16 25 36 49 64 81 )

Example: Algorithms

Traditionally, the next topic should be a lengthy discussion of algorithms for searching, sorting, and transforming arrays. Fortunately, the C++ standard library provides generic functions for doing most of these tasks. We begin by including the header file containing these generic algorithms:

#include <algorithm>
using namespace std;

The reader will need to consult documentation on these functions as only a few are covered here. They are also discussed at greater length in the chapter of the standard library.

Most of these functions expect the start and end of the array to be specified using pointers. For example, here's how an array can be sorted:

sort(mt1, mt1 + 5);
print(mt1, 5); cout << endl; // prints ( 18 45 78 88 93 )

We can search an array using the find function. The following statements:

int* p = find(mt2, mt2 + 10, 25);
if (p != mt2 + 10) cout << "found = " << *p << endl;
else cout << "not found\n";
p = find(mt2, mt2 + 10, 26);
if (p != mt2 + 10) cout << "found = " << *p << endl;
else cout << "not found\n";

produce the output:

found = 25
not found

Of course the pointers don't need to point to the beginning and end of the array. They can point to the middle of the array if desired. The following statements:

reverse(mt2, mt2 + 5);
print(mt2, 10); cout << endl;

produce the output:

( 16 9 4 1 0 25 36 49 64 81 )

Some library functions expect another function as a parameter. For example, assume the following three functions have been defined:

bool even(int n) { return n % 2 == 0; }
int cube(int n) { return n * n * n; }
void printNum(int i) { cout << i << ' '; }

We could redefine our print function using the for_each library function:

void print2(int vals[], int size)
{
cout << "( ";
for_each(vals, vals + size, printNum);
cout << ")";
}

The following statements:

print2(mt1, 5); cout << endl;
print2(mt2, 10); cout << endl;

produce the output:

( 18 45 78 88 93 )
( 16 9 4 1 0 25 36 49 64 81 )

The count_if function counts the number of items that pass a test, which is provided as a parameter. The following statement:

cout << "count = " << count_if(mt2, mt2 + 10, even) << endl;

produces the output:

count = 5

The transform function has the signature:

transform(srcStart, srcEnd, destStart, transformer)

where:

srcStart = start of source array
srcEnd = end of source array
destStart = start of destination array
transformer = function used to transform array members

The algorithm will figure out where the end of the destination array will be. We can identify the source and destination arrays if we want to transform an array in place. For example, the statements:

transform(mt2, mt2 + 10, mt2, cube);
print2(mt2, 10); cout << endl;

produce the output:

( 4096 729 64 1 0 15625 46656 117649 262144 531441 )

Example: Dynamic Arrays

A common task is to allow users to add and remove items from a array. Since we can't anticipate how many items will eventually end up in the array, we use a dynamic array. In the following example, we reuse our CUI control loop to allow users to add and remove names of cities (sorry, no white space allowed). Here are the commands:

add CITY
rem CITY
display

Here's a sample run:

type "quit" to quit
-> add LA
done
-> add SF
done
-> add Boston
done
-> add LA
done
-> add NYC
done
-> add Atlanta
growing the cities array
done
-> add Fresno
done
-> display
LA SF Boston LA NYC Atlanta Fresno
done
-> rem LA
done
-> display
SF Boston NYC Atlanta Fresno
done

Our program begins with a few pre-processor directives:

#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
#define BLOCK_SIZE 5

We use global variables to hold important data:

int capacity = BLOCK_SIZE;
int size = 0;
string* cities = new string[BLOCK_SIZE];

Here's our execute function:

string execute(string cmmd)
{
string city;
if (cmmd == "add")
{
cin >> city;
grow();
cities[size++] = city;
}
else if (cmmd == "rem")
{
cin >> city;
string* end = cities + size;
string* newEnd = remove(cities, end, city);
size -= int(end - newEnd);
}
else if (cmmd == "display")
{
for_each(cities, cities + size, displayCity);
cout << endl;
}
else
{
cerr << "Error: unrecognized command: " << cmmd << endl;
cin.sync(); // flush buffer
}
return "done";
}

Displaying a city is trivial:

void displayCity(string city)
{
cout << city << ' ';
}

The grow function grows the cities array in necessary:

void grow()
{
if (capacity <= size)
{
cout << "growing the cities array\n";
capacity += BLOCK_SIZE;
string* temp = new string[capacity];
for(int i = 0; i < size; i++)
temp[i] = cities[i];
delete[] cities;
cities = temp;
}
}

Vectors

Arrays have two problems. First, C++ does not automatically validate indices. Instead, the program just crashes, or worse, memory is corrupted:

double vec[3] = {100, 200, 300};
vec[4] = 0; // oops!

Second, arrays can't expand to accommodate more elements. A length three array is always a length three array.

To solve these problems the standard C++ library includes a vector class. Actually, vector is not a class, it's a template for generating classes. For example, here is how we would declare different types of vectors:

vector<double> vec1, vec2, vec3;
vector<vector<double> > mat1, mat2;
vector<char> msg1, msg2, msg3, msg4;

(Note the space after the second angle bracket in the middle declaration. This is necessary to prevent confusion with the right shift operator.)

We can add as many elements as we want to vec1:

vec1.push_back(7);
vec1.push_back(42);
vec1.push_back(19);
vec1.push_back(100);
vec1.push_back(-13);

We can access the members of vec1 using subscripts:

int n = vec1.size();
for(int i = 0; i < n; i++)
vec1[i] = vec1[i] * 2;

Unfortunately, the subscript operator, [], doesn't validate index bounds, we need the at() function encapsulated by vec1 for that:

try
{
cout << vec1.at(500); // oops!
}
catch(out_of_range e)
{
cerr << e.what() << '\n';
}

To make vectors available to our programs, we must include the vector header file:

#include <vector>
using namespace std;

Iterators

Officially, vectors, in fact all of the container templates, use iterators as abstract pointers. We aren't allowed to know what an iterator is, but here's how one is declared:

vector<double>::iterator p;

All vectors encapsulate iterators that point to the first element and just beyond the last element:

vec1.begin(); // points to beginning of vec1
vec1.end(); // points to just beyond the end of vec1

An iterator can be incremented or decremented using the ++ and -- operators. The element an iterator p points to can be accessed by dereferencing the iterator using the unary * operator. Putting all this together, here's another way to traverse vec1:

for(p = vec1.begin(); p != vec1.end(); p++)
cout << *p << ' ';

Example: Using Algorithms with Vectors

We repeat our scores example using vectors. Of course we must remember our include directives:

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

Here is how the vectors are declared and initialized:

vector<int> mt1, mt2;
mt1.push_back(78);
mt1.push_back(93);
mt1.push_back(45);
mt1.push_back(18);
mt1.push_back(88);

for(int i = 0; i < 10; i++)
mt2.push_back(i * i);

The vector versions of average and print don't need to have the sizes of the vectors passed as parameters. This can be determined by calling the size function:

double avg(vector<int> scores)
{
int total = 0;
for(int i = 0; i < scores.size(); i++)
total += scores[i];
return double(total)/double(scores.size());
}

void print(vector<int> scores)
{
cout << "( ";
for(int i = 0; i < scores.size(); i++)
cout << scores[i] << ' ';
cout << ")";
}

The following statements:

cout << "avg1 = " << avg(mt1) << endl;
cout << "avg2 = " << avg(mt2) << endl;
print(mt1); cout << endl;
print(mt2); cout << endl;

produce the output:

avg1 = 64.4
avg2 = 28.5
( 78 93 45 18 88 )
( 0 1 4 9 16 25 36 49 64 81 )

We saw earlier that the generic functions in the standard library generally required three inputs: a pointer to the start of the source, a pointer to the end of the source, and sometimes a function to process or test the individual members. The generic functions are so generic that the source can be a vector (or a list, map, set, etc.) and iterators can be pointers.

Here's the vector version of print2:

void print2(vector<int> vals)
{
cout << "( ";
for_each(vals.begin(), vals.end(), printNum);
cout << ")";
}

Executing the statements:

vector<int>::iterator p = find(mt2.begin(), mt2.end(), 25);
if (p != mt2.end()) cout << "found = " << *p << endl;
else cout << "not found\n";

p = find(mt2.begin(), mt2.end(), 26);
if (p != mt2.end()) cout << "found = " << *p << endl;
else cout << "not found\n";

reverse(mt2.begin(), mt2.begin() + 5);
print2(mt2); cout << endl;

cout << "count = "
cout << count_if(mt2.begin(), mt2.end(), even) << endl;

transform(mt2.begin(), mt2.end(), mt2.begin(), cube);
print2(mt2); cout << endl;

sort(mt1.begin(), mt1.end());
print2(mt1); cout << endl;

produces the output:

found = 25
not found
( 16 9 4 1 0 25 36 49 64 81 )
count = 5
( 4096 729 64 1 0 15625 46656 117649 262144 531441 )
( 18 45 78 88 93 )