Emergence

State Space

Agent States

Agents can be stateful. This means that an agent can have an internal state that changes over time. For example, the state of an agent could be a model of the environment stored in the agent's memory. As the agent learns new things about its environment, it gradually improves this model.

The state space of an agent is the set of all possible states the agent can have. For example, if the state of an agent is its position and momentum, and if these are both real numbers between -1 and 1, then the state space of the agent would be:

AgentStates = [-1, 1] x [-1, 1]

ABS- Micro States

An agent-based system (ABS) is also stateful. In this case we must distinguish between its microstate and its macro-state. The microstate of an ABS is the list of agent states for all agents in the system. (We assume the agents have some natural order.) The Micro-State Space for an ABS is the set of all possible microstates. If there are N agents, and if all agents have the same agent state space, then the microstate space of the ABS would be the set of all N-dimensional vectors over the agent space:

MicroStates = AgentStates^N

ABS- Macro States

Sometimes the microstate space of an ABS can be partitioned into macro-states. In statistical mechanics every microstate has a probability of occurring:

probability: MicroStates -> [0, 1]

A macro-state corresponds to all microstates s such that probability(s) = p for some fixed value of p.

Of course any function f can be used to define a partition of microstates into macro-states.

Macro-states often have observable properties like temperature, color, and firmness.

Example

Assume the state of an agent in an artificial society is his financial statement: income, investments, expenses, etc. The microstates of the society consist of the aggregation of the financial statements of all of its members. The macro-states might correspond to the average income of the society. Economic phenomena like inflation and recession might be considered macro-macro-states.

Behavior

Assume the state of agent A at time t is:

state_A(t)= s_t

If the agent is born at time t = 0 and dies at time t = N, then the list of states:

(s₀, s₁, s₂, ..., s_N)

is called the agent's trajectory or behavior.

In a similar way can define the microstate and macro-state behaviors/trajectories of an ABS.

Behavioral Patterns

The behavior of an agent or an ABS might exhibit a pattern. For example, a behavior might contain a repeating sequence of states. Patterns can be simple or complicated. These issues are elaborated on in Cascades.

Emergent Behavior

One problem of dynamical systems theory is relating the microstate behavior of a cascade to its macro-state behavior and vice-versa. In a sense this problem is analogous to integration (deducing global behavior from local behavior) and differentiation (deducing local behavior from global behavior).

Sometimes the macro-state behavior of an ABS exhibits a pattern that seems unrelated to the microstate behavior. In these cases we say that the macro-state pattern emerges from the microstate behavior.

Example: Mosaics

The concept of emergence can also be applied to mapping microstates to macro-states. Knowing the microstate often doesn't help us to know the macro-state. For example, we can think of a mosaic as a collection of monochromatic tiles (the agents). Only when we step back far enough from the mosaic do we see the macro-state: a photo of the Matterhorn!

Example: Science

Physics studies the properties (mass momentum, spin, etc.) of subatomic particles. A complete description of the microstate/behavior of the world would include the state of every particle.

Chemistry studies the macro-state/behavior of the world: the chemical properties of atoms and molecules.

Biology studies the macro²-state/behavior of the world: the biological properties of cells and organisms.

Psychology studies the macro³-state/behavior of the world: the properties of brains and minds.

Sociology studies the macro4-state/behavior of the world: the properties of societies of brains and minds.

Example: The Law of Large Numbers (LLN)

Assume every agent in a population of N agents is assigned a random value between 1 and 6. Let V_N be the average of these values. The Law of large Numbers states that as N increases, V_N will approach the expected value:

(1 + 2 + 3 + 4 + 5 + 6)/6 = 21/6 = 3.5

We can demonstrate this with a simple NetLogo program. Each time the "update 100x" button is pressed, 100 random numbers are added to a list. The value of V_N is plotted against the value of N. Here's the graph as N approaches 121:

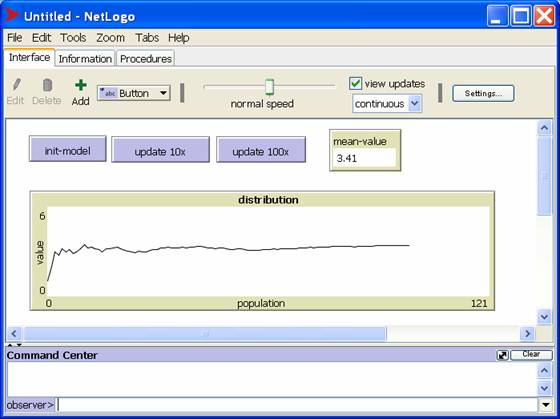
Note that V_N varies wildly for small values of N, but as N gets larger, the graph begins to level out.

As N approaches 900, we see that V_N gets very close to 3.5:

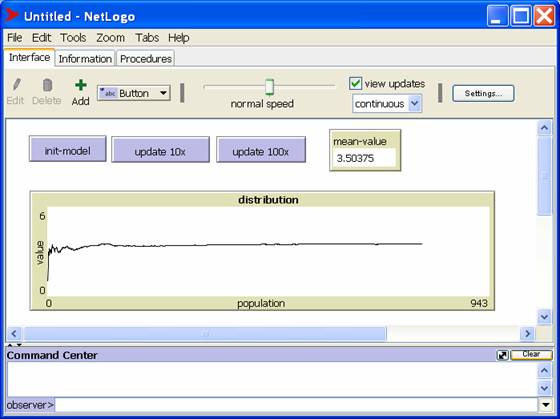
The Law of Large Numbers is a simple yet pervasive example of emergence. No agent actually has the value 3.5, yet as more agents are added to the population, their values begin to cancel each other out, so V_N, the macro-state, begins to converge to 3.5.

More Examples

Computers

Brains

Example: Power Laws

Consider the formula:

freq(x) = # of agents with state = x

In NetLogo:

to-report freq[x]
report count agents with [state = x]
end

We can consider the graph (or histogram) of freq(x) to be a snapshot of the macro-state of some system.

For example, we would expect freq(x) to be almost constant in a population in which states are randomly distributed. In other words, there should be N agents in state 1, N in state 2, etc.

We would expect the graph of freq(x) to be a bell curve if states were distributed using random-normal.

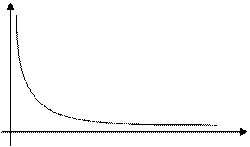
In some important natural cases freq(x) has the general form:

freq(x) = a * x^-k

This is called the power law or inverse exponential.

In this case the graph has the form:

Zipf's Law

A concordance gives the word frequency of some document, The Harvard Shakespeare Concordance, for example.

If we order the words in a concordance according to frequency, then according to Zipf's Law, the frequency of the word in position k will be approximately:

freq(k) = k^-1

Pareto's Law

Pareto's Law, also called the 80-20 law, says 80% of the effects come from 20% of the causes.

For example, 80% of the sales come from 20% of the customers, 80% of the work is done by 20% of the people, 80% of the crimes are committed by 20% of the criminals, 80% of the wealth belongs to 20% of the people, etc.

The Pareto Distribution is a power law. For example, let the state of an agent be his wealth, then

freq(x) = # of agents with wealth > x

is approximated by the power law:

freq(x) = x^-k

More Examples

Here are some other examples from nature that follow the power law distribution:

magnitudes of earthquakes

city sizes

file sizes

sizes of forest fires

sizes of oil fields

etc.

Example: Tipping Points, Phase Transitions, Self-Organized Criticality (SOC)

A phase is a set of similar macro-states.

Example: solid, liquid, and gas are the phases of matter.

Example: sitting and standing are the phases of an audience.

In a complex system SOC occurs when micro-behavior naturally leads to a macro-state that is critical in the sense that something that happens at the micro-level can cause a phase transition.

Adding grains of sand to a sand pile is an example. As the sand pile reaches a certain angle of repose, adding another grain can cause an avalanche. Furthermore, an avalanche can cause avalanches in neighboring piles. This can lead to a cascade of avalanches. If we graph the number of grains displaced, we get a power law distribution:

freq(x) = frequency of an avalanche in which x grains of sand are displaced = x^-k

The phenomenon was first applied to sociology when sociologists noticed white flight from neighborhoods when the number of non-white families reached a critical number.

Model Library

All of the models exhibit emergence. Try these

biology/termites

social science/distribution of wealth

social science/El Farol