Outline

• Set Cover Approximation
• Randomized Walks for 2-SAT
• Quiz
• Randomized Approximation Algorithms

Introduction

• Last week, we began talking about approximation algorithms for NP-complete problems.
• Given an NP-complete problem, say 3-SAT. We look at the associated optimization problem, in this case, trying to satisfy the most clauses. Then we try to come up with good algorithms for it. I.e., both `p`-time and a good approximation.
• Let `C` denotes our algorithm's solution. For 3-SAT this would be the number of clauses our algorithm satisfies. Let `C^{\star}` denote the best possible value. We defined `max(C/C^{star}, C^{star}/C)` as the approximation ratio of our algorithm.
• We gave p-time, 2-approximation algorithms for VERTEX-COVER and Euclidean TSP, however, we showed that for general TSP, if there was an a `m gt 0` such that it was `m`-approximable in `p`-time then we could solve HAM-CYCLE, and hence, `P=NP`.
• We start today by looking the SET-COVER problem and use it as an example where we can get an approximation, but it is not to within a constant factor.

The Set Covering Problem

• Set covering was one of the 21 `NP`-complete problems given by Karp in 1972.
• It models a variety of resource selections problems.
• An instance `(X, F)` of the set covering problem consists of a finite set `X` and a family of subsets of `X`, `F`, such that every element of `X` belongs to at least one subset of `F`. I.e., `X = cup_(S in F) S`.
• We say that a subset of `S in F` covers its elements.
• The set cover optimization problem is to find a minimum-sized subset `C subseteq F` whose members cover all of `X`. I.e., `X = cup_(S in C) S`.
• In the above picture, we have a set `X` of 12 elements, and we have a set `F = {S_1, ..., S_6}` of subsets of `X`. The set `C={S_3, S_4, S_5}` is a minimal cover.
• The NP-complete decision problem is to determine if `(X, F)` has a set cover of size `k`.

Example Uses of Set Cover

• Suppose `X` represents a set of skills that are needed to solve a problem.
• `F` might be a set of people each of which have some of these skills.
• We might want to find a team `C` of as few people as possible that together have all the skills needed to solve the problem.
• As another example, you could imagine trying to come up with a summary for a document based on the smallest set of sentences in the document that contain all the distinct words in the document.

Greedy Algorithm For Set Covering

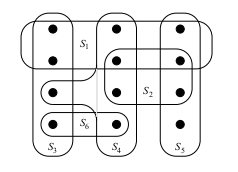
One can give a greedy algorithm for finding a cover by picking the set `S` at each stage that covers the greatest number of remaining elements that are uncovered.

GREEDY-SET-COVER(X, F)
1 U := X
2 C := ∅
3 while U ≠ 0
4     select an S ∈ F that maximizes {S ∩ U}
5     U := U - S
6     C := C ∪ {S}
7 return C

Approximation Result for Set Cover

Let `H(d) = sum_(i=1)^d 1/i` denote the `d`th harmonic number, defining `H(0) = 0`.

Theorem. GREEDY-SET-COVER is a polynomial-time `r(n)`-approximation algorithm, where
`r(n) = H(max{|S| : S in F})` on instances `(X,F)` or size `n`.

Proof. GREEDY-SET-COVER deletes at least one `S` from `F` in each iteration and the select step is at most quadratic time, so the algorithm will be polynomial time in the instance size.

To see that GREEDY-SET-COVER is an `r(n)`-approximation algorithm, we assign a cost of `1` to each set selected by the algorithm, distribute this cost over the elements covered for the first time, and then use these costs to derive the desired relationship between the size of an optimal set cover `C^star` and the size the cover `C` returned by the algorithm...

Proof of Approximation Result for Set Cover cont'd

Let `S_i` denote the `i`th set selected by GREEDY-SET-COVER. We spread the cost of selecting `S_i`, 1, evenly among the elements covered for the first time by `S_i`. Let `c_x` denote the cost allocated to element `x in X`. If `x` is covered by `S_i`, then
`c_x = 1/(|S_i - (S_1 cup S_2 cup ... cup S_(i-1))|)`.
At each step of the algorithm, 1 unit of cost is assigned, and so
`|C| = sum_(x in X)c_x`.
The cost of the optimal cover is `sum_(S in C^star)sum_(x in S)c_x`,
and as each `x in X` is in at least one `S in C^star`, we have
`sum_(S in C^star)sum_(x in S)c_x ge sum_(x in X)c_x = |C|` (**).

We will show the theorem follows from the following claim:

Claim.`sum_(x in X)c_x le H(|S|)` for all `S in F`.

(Proof of Theorem from Claim). From (**) and the claim, we have
`|C| le sum_(S in C^star) H(|S|)`
`le |C^star| cdot H(max{|S| : S in F})`

Proof of Element Cover Cost Claim

Consider any `S in F` and `i = 1, ..., |C|`. Let
`u_i = |S - (S_1 cup S_2 cup ... cup S_(i))|`.
We define `u_0 = |S|`. Let `k` be the least index such that `u_k = 0`. At `k`, each element in S will be covered by at least one of `S_1, ... S_k`. We have `u_(i-1) ge u_i`, and that `u_(i-1) - u_i` elements of `S` are covered for the first time by `S_i`. Thus,
`sum_(x in S)c_x = sum_(i = 1)^k(u_(i-1) - u_i) cdot 1/(|S - (S_1 cup S_2 cup ... cup S_(i -1))|)`
Observe that
`|S_i - (S_1 cup S_2 cup ... cup S_(i - 1))| ge |S - (S_1 cup S_2 cup ... cup S_(i - 1))| = u_(i - 1)`
because we chose `S_i` greedily. This gives
`sum_(x in S)c_x le sum_(i = 1)^k(u_(i-1) - u_i) cdot 1/(u_(i-1))`
`= sum_(i=1)^k sum_(j = u_i + 1)^(u_(i-1))1/(u_(i-1))`
`le sum_(i=1)^k sum_(j = u_i + 1)^(u_(i-1)) 1/j` (because of the start condition of sum, `j le u_(i-1)`)
`= sum_(i=1)^k ( sum_(j = 1)^(u_(i-1)) 1/j - sum_(j = 1)^(u_(i)) 1/j)`
`= sum_(i=1)^k (H(u_(i-1)) - H(u_i))`
`= H(u_0) - H(u_k)` (telescoping series)
`= H(u_0) - H(0)`
`= H(u_0)`
`=H(|S|)`, proving the claim.

Random Walks for SAT

• Consider the following algorithm for satisfiability:
  1. Start with any truth assignment `T`, and repeat the following `r` times:
     1. If there is no unsatisfied clause output "Satisfiable", halt.
     2. Otherwise, take any unsatisfied clause; pick any of its literals at random and flip its value
  2. After `r` repetitions reply "the formula is probably unsatisfiable"
• Is there a good value of `r` to choose so that this algorithm works?

Random Walks for 2SAT

Theorem. Suppose that the random walk algorithm with `r=2n^2` is applied to any satisfiable instance of 2SAT with `n` variables. Then the probability that a satisfying truth assignment will be discovered is at least `1/2`.

Proof. Let `T` be a truth assignment which satisfies the given 2SAT instance `I`. Let `t(i)` denote the number of expected repetitions of the flip step until a satisfying assignment is found starting from an assignment `T'` which differs in at most `i` positions from `T`. Notice:

1. `t(0) = 0`
2. If we find some other satisfying assignment, we do not need to continue.
3. Otherwise, we flip at least once, and we have a 50% chance of moving closer to the solution; 50% farther. So `t(i) le 1/2(t(i-1) + t(i+1)) + 1`
4. We also have `t(n) le t(n-1) + 1` (If every literal is wrong, we can only move closer).

The worst case is the when relation `t` of (3) and (4) hold as equations. `x(0)=0`; `x(n)=x(n-1)+1`; `x(i) = 1/2(x(i-1)+x(i+1))+1`

Proof Cont'd

• As you can see above, adding all the `x(i)`'s together gives: `x(1) = 2n-1`.
• Then solving the `x(1)` equation for `x(2)` gives `4n-4`, and in general, `x(i) =2 i n-i^2`.
• Thus we have shown `t(i) le x(i) le x(n)=n^2`. Now consider the following lemma:
  Lemma (Markov Inequality). If `x` is a random variable taking nonnegative integer values, then for any `k > 0`, `Pr[x ge k cdot E(x)] le 1/k`.
  Proof. Let `p_i` be the probability that `x=i`.
  `E(x) = sum_i i cdot p_i = sum_(i le k cdot E(x)) i cdot p_i + sum_(i > k cdot E(x)) i cdot p_i > k cdot E(x) cdot Pr[x>k cdot E(x)]` Q.E.D.
• The theorem then follows taking `k=2`.

Quiz

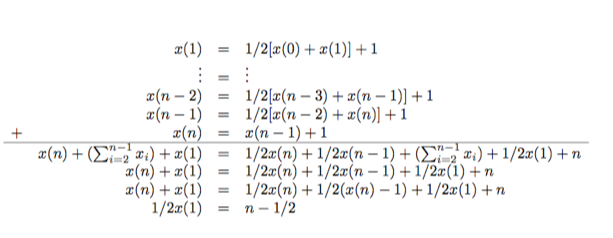
Which of the following statements is true?

1. To show TSP was NP-complete in-class we used a reduction from SUBSET-SUM.
2. Our 2-approximation algorithm for VERTEX COVER made use of minimal spanning trees.
3. We showed if `P ne NP` then there is no p-time approximation algorithm for TSP.

Randomized Approximation Algorithms

• We say a randomized algorithm for a problem has an approximation ratio of `r(n)` if for any input size `n`, the expected cost `C` of the solution produced by the randomized algorithm is within a factor of `r(n)` of the cost `C^star` of an optimal solution.
• We call a randomized algorithm that achieves an approximation ratio of `r(n)` a randomized `r(n)`-approximation algorithm.
• Let MAX-kSAT be the problem of determining given a `k`-CNF formula an assignment which makes as many clauses as possible evaluate to `1`.

Algorithm for MAX-3SAT

Theorem. Given an instance of MAX-3SAT with n variables and `m` clauses, the randomized algorithm that independently sets each variable to `1` with probability `1/2` and to `0` with probability `1/2` is an randomized `8/7`-approximation algorithm.

Proof. Define the indicator random variable `Y_i = I{`clause `i` is satisfied`}`. Since no literal appears more than once in the same clause, and since we assume that no variable and its negation appear in the same clause, the settings of the three literals are independent. A clause is not satisfied only if all three of its literals are set to `0`. We thus have:

1. `Pr{ mbox{clause } i mbox( is not satisfied ) } = 1/8`
2. `Pr{ mbox{clause } i mbox( is satisfied ) } = 7/8`.
3. `E[Y_i] = 7/8`.

Let `Y = sum_i Y_i`. Then
`E[Y] = E[sum_i Y_i] = sum_iE[Y_i] = sum_i 7/8 = (7m)/8`.
As `m` is an upper bound on the number of possible clauses that could be satisfied, this gives the result.