Introduction

We have been talking about Parallel Random Access Machines as a model for parallel processing.
A PRAM consists of a shared set of integer registers and a collection of processors with access to these registers, using the same instruction set and running the same program, but each with its own set of integer accumulators and program counter.
On Monday, we introduced the complexity classes `NC^k` for decision procedures that can be carried out on a PRAM using polynomial in the input size `n` many processors and at most `O(log ^k n)` depth. We said `NC = cup_k NC^k`.
We also gave one-sided and zero error randomized variants of these classes `RNC` and `ZNC`.
Then we gave a ZNC algorithm for sorting called BoxSort and analyzed its complexity.
Today, we look at a second randomized PRAM algorithm, this time for computing a maximal independent set in a graph.

Maximal Independent Set

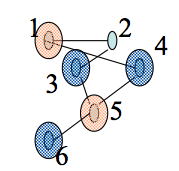
Let `G = (V,E)` be an undirected graph with `n` vertices and `m = Omega(n)` edges. A subset `I` of `V` is said to be independent in `G` if no edge in `E` has both ends in `I`.
Equivalently, if `Gamma(v)` is the set of vertices connected to `v`, then `I` is independent if for all `v in I`, `Gamma(v) cap I = emptyset`.
An independent set is maximal if it is not a proper subset of another independent set in `G`.
The red nodes and the blues nodes in the graph above are two different maximal independent sets in the same graph. Notice the blue set has more nodes.
The problem of finding a maximum independent set (the independent set with the most nodes) is NP-hard.

In contrast the finding a maximal independent set is `O(m)` time:

Greedy MIS:
Input: Graph G(V,E) with V = {1,..,n}
Output A maximal I contained in V.
1. I := emptyset
2. For v=1 to n do
3.     If Gamma(v) intersect I = emptyset then I := I union {v}.

Analysis of Greedy MIS

Greedy-MIS is very sequential in nature.
For the graph on the last slide the algorithm outputs the Maximal Independent Set (MIS) {1,3,6}.
Notice the two other independent sets we had previously drawn are {1,5} and {3, 4, 6}. According to dictionary (lexicographical) order {1, 3, 6} is before {1,5} is before {3, 4, 6}.
It turns out Greedy-MIS always outputs the lexicographically first MIS (LFMIS).
LFMIS is a P-complete problem (with respect to log-time poly- processor PRAM reductions) (Cook 1985).
So it is known that an NC algorithm for LFMIS would imply P=NC. (This is an open problem. In English, it asks does every poly-time algorithm have a good parallel one?)
We will describe an RNC algorithm for MIS and later show how to derandomize it to an NC algorithm.
The maximal set we output won't typically be the lexicographically first one.

Towards a Parallel MIS Algorithm

Consider the following variant of Greedy MIS, where, we after setting `I = emptyset` in the for loop, we do:
```
1. Pick any vertex v
2. Add v to I 
3. Delete v and Gamma(v) from the graph.
```
Choosing `v` to be the lowest numbered vertex present in the graph is the Greedy MIS algorithm.
The basic idea of our parallel algorithm is to generalize this to find an independent set `S`, add `S` to `I` and delete `S` and `Gamma(S)`.
We want to choose an independent set such that `S cup Gamma(S)` is large to keep the number of iterations small.
To do this we ensure the number of edges incident to `S cup Gamma(S)` is a large fraction of the total remaining edges.
To find such an `S`, we pick a large random set of vertices `R` contained in `V`. `R` won't usually be independent. If we bias the sampling in favor of vertices with low degree, we can hope that few will have both endpoints in `R`. For those edges which have both endpoints in `R`, we delete the one of lower degree. This gives an independent set.

Parallel MIS

Input: G=(V,E)
Output: A maximal independent set I contained in V
1. I := emptyset
2. Repeat {
   a) For all v in V do in parallel
         If d(v) = 0 then add v to I and delete v from V.
         else mark v with probability 1/(2d(v)).
   b) For all (u,v) in E do in parallel
         if both u and v are marked
             then unmark the lower degree vertex.
   c) For all v in V do in parallel
         if v is marked then add v to S
   d) I := I union S
   e) Delete S union Gamma(S) from V and all incident edges from E 
   } Until V is empty.

In-Class Exercise

Step-by-step simulate the execution of this algorithm by hand on the graph we gave on slide 4.
Use coin flips as needs to handle places where randomness is used.
Please post your solutions to the Mar 2 In-Class Exercise Thread.

Analysis of Parallel MIS

The Parallel MIS algorithm and the analysis we give are due to (Luby 1986).
Each iteration of the above takes `O(log n)` time on an EREW PRAM with `O(n+m)` processors.
We want to bound the number of iterations we do.
Call a vertex `v` good if it has at least `(d(v))/3` neighbors of degree no more than `d(v)`; otherwise, the vertex is bad. An edge is good if one of its endpoints is good and is bad otherwise.
A good vertex is quite likely to have one of its lower degree neighbors in S and so is likely to be deleted from `V`.
We argue that the number of good edges is large, and since good edges are likely to be deleted, a large number of edges will be deleted each iteration.

More Analysis of Parallel MIS

Lemma*. Let `v` in `V` be a good vertex with degree `d(v) > 0`. Then, the probability that some vertex `w in Gamma(v)` gets marks is at least `1- exp(-1/6)`.

Proof. Each vertex `w in Gamma(v)` is marked independently with probability `1/(2d(w))`. Since `v` is good, there exist `(d(v))/3` vertices in `Gamma(v)` with degree at most `d(v)`. Each of these is marked with probability at least `1/(2d(v))`. Thus, the probability none of these neighbors is marked is at most: `(1 - 1/(2d(v)))^((d(v))/3) le e^((-1)/6)`.

Here we are using that `(1 + a/n)^n <= e^(a)` and that the remaining neighbors of `v` can only help increase the probability under consideration.

Yet More Analysis of Parallel MIS

Lemma**. During any iteration, if a vertex `w` is marked then it is selected to be in `S` with probability at least `1/2`.

Proof. The only reason a marked vertex `w` becomes unmarked and hence not selected for `S` is if one of its neighbors of degree at least `d(w)` is also marked. Each such neighbor is marked with probability at most `1/(2d(w))`, and the number of such neighbors is at most `d(w)`. Hence, we get the probability that a marked vertex is selected to be in `S` is at least:
`1 - Pr{exists x in Gamma(w) mbox( such that ) d(x) ge d(w) mbox( and x is marked )}`
`ge 1 - |{x in Gamma(w)| d(x) ge d(w)}| times 1/(2d(w))`
`ge 1 - sum_(x in Gamma(w))1/(2(d(w))`
`= 1 - d(w) times 1/(2(d(w))`
`= 1/2`

Even More Analysis of Parallel MIS

Lemma#. The probability that a good vertex belongs to `S cup Gamma(S)` is at least `(1- exp(-1/6))/2`.

Proof. Let `v` be a good vertex with `d(v) > 0`, and consider the event `E` that some vertex in `Gamma(v)` does get marked. Let `w` be the lowest numbered marked vertex in `Gamma(v)`. By Lemma **, `w` is in `S` with probability at least `1/2`. But if `w` is in `S`, then `v` belongs `S cup Gamma(S)` as `v` is a neighbor of `w`. By Lemma *, the event `E` happens with probability `1- exp(-1/6)`. So the probability `v` is in `S cup Gamma(S)` is thus `(1- exp(-1/6))/2`.

Parallel MIS - Distributed Algorithms

Outline