Outline

• Axis Angle Representation of Rotations
• In-Class Exercise
• Quaternions and Spherical Linear Interpolation

Introduction

• On Monday, we started talking about the matrices needed to place an object in a VR scene and then eventually render the scene for each eye.
• We said how to do translations in 3D: `(x, y, z) mapsto (x + x_t, y + y_t, z + z_t)`
• We said how to represents 2D points `(x,y)` as complex numbers `x + iy` and then convert these to polar coordinates `re^{i theta}`.
• We said that a counter-clockwise rotations in the complex plane by `phi`, can be done by multiplying each point in a scene `e^{i phi}`.
• If we write out this operation as a `2 times 2` matrix we get: `((cos phi, -sin phi),(sin phi, cos phi))`.
• We then said in 3D any rotation can be described in terms of a product of rotations about the `x` (pitch), `y` (yaw), `z` (roll), the matrices for which were easily described in terms of `2 times 2` rotation matrices.
• Finally, we said that we can combine a 3D rotation and a translation into a single `4 times 4` homogeneous transformation matrix `T_{rb}` as:
  
• Today, we start by looking at the Axis-Angle Representation of rotations.

Axis-Angle Representations of Rotations

• Currently, our description of rotation in 3D is as a product of three matrices: `R(alpha, beta, gamma) = R_y(alpha)R_x(beta)R_z(gamma)`.
• This product has nine matrix entries determined by only the three rotation parameters and the operations are not commutative.
• To understand how any 3D rotation is given by three rotations as above, notice any rotation in 3D fixes an axis (Euler's Rotation Theorem), and so can be described by the axis of rotation, followed by the angle to rotate.
• The axis can be determined by a fixed vector on the unit sphere. Such a point can be described by its longitude and latitude.
• So we can imagine we do our rotation about the unit `z` vector, then rotating the `z` vector so it points along the axis we wanted to rotate.
• We can use a rotation about `x` to map the `z` vector to a given latitude, then we can rotate about `y` to move to a give longitude.
• Combinations of `x` pitch and `y` yaw rotations can cause problems, basically, because the poles on the unit sphere have every possible longitude. These combinations can cause rotating objects in a scene to get stuck in a phenomena, known as gimbal lock.
• This problem is avoided if we can stick to viewing rotations as purely axis and angle.
• This representation is also better if we want to spherically linearly interpolate (slerp) between two angles, such as when we want to rotate a car wheel.

Quaternions

• Quaternions are a generalization of complex numbers which can be used to provide to represent our axis angle description of rotations.
• Quaternions were first described by Hamilton in 1843 and were used by Maxwell when he first gave his equations for eletromagnetism.
• Vectors in physics were championed by Oliver Heaviside who recast Maxwell's equations in a simplified form using them. This became more popular, and in non-math settings, quaternions fell out of favor except for things like early 5D attempts at quantum gravity.
• A quaternion is a 4-tuple of real numbers, on which we will define suitable operations.
• We write a quaternion as:
  `[[w],[hat bb c]]`
  where `w` is a scalar and `hat bb c` is a coordinate 3-vector. We are using the hat on the `c` so we don't confuse it with a 4-vector.
• A quaternion of the form `[[0],[hat bb c]]` is called pure, and can be thought as the quaternionic setting notion corresponding to a pure imaginary number in the complex number setting.

Quaternion Rotations

• To represent a rotation of `theta` degrees about a unit length axis `hat bb k` we use the quaternion:
  `[[cos(theta/2)],[sin(theta/2)hat bb k]]`
  It turns out the dividing by 2 in the rotation makes the quaternion operations that we'll describe work out properly.
• Notice a rotation of `-theta` about the axis `- vec bb k` gives us the same quaternion.
• Also, a rotation `theta + 4 pi` about an axis `vec bb k` gives us the same quaternion.
• One thing that will slightly complicate our power operation is that a rotation of `theta + 2pi` about an axis `vec bb k` gives us the negated quaternion
  `[[-cos(theta/2)],[-sin(theta/2)hat bb k]]`

Some Special Cases and Terminology

• The quaternions
  `[[1],[hat bb 0]], [[-1],[hat bb 0]]`
  represent the identity rotation matrix.
• The quaternions
  `[[0],[hat bb k]], [[0],[-hat bb k]]`
  represent a 180-degree rotation about `hat bb k`.
• Any quaternion of the form:
  `[[cos(theta/2)],[sin(theta/2)hat bb k]]`
  has a norm (square root of the sum of squares of the four entries) of 1.
• Conversely, any such unit norm quaternion can be interpreted as a unique rotation matrix.

Operations

• Multiplication of a quaternion by a scalar is defined as:
  `alpha [[w],[hat bb c]] = [[alpha w],[alpha hat bb c]]``
• Multiplication of two quaternions is defined by:
  `[[w_1],[hat bb c_1]][[w_2],[hat bb c_2]] = [[(w_1w_2 - hat bb c_1 cdot hat bb c_2)],[(w_1hat bb c_2 + w_2hat bb c_1 + hat bb c_1 times hat bb c_2)]]`.
  Here `cdot` is dot product and `times` is cross product.
• This seemingly strange multiplication has the property that if `[w_i, vec bb c_i]^t` represent rotation matrices `R_i` then their product represents the `R_1R_2`. This can be verified by direct (not necessarily intuitive) calculation.
• The length of a quaternion is `||[w, hat bb c ]^t|| = sqrt(w^2 + x^2 + y^2 + z^2)` where `hat bb c = (x,y,z)`.
• We defined scalar multiplication of quaternions as `alpha [w, x, y, z]^t = [alpha w, alpha x, alpha y, alpha z]^t = [alpha w, alpha hat bb c ]^t`.
• So letting `u = 1/(||[w, hat bb c ]^t||)[w, hat bb c ]^t`. We see any quaternion can we written in the form `s cdot u` where `s` is a scalar length and `u` is a quaternion of length `1`, a unit quaternion. This is similar to the fact that every complex number `z` can be written in polar form `z = r e^(i theta)`.
• Given a unit norm quaternion its inverse can be shown to be:
  `[[cos(theta/2)],[sin(theta/2)hat bb k]]^(-1) = [[cos(theta/2)],[-sin(theta/2)hat bb k]]`

In-Class Exercise

• Consider the two quaternions: `[[1],[2],[3],[4]]`, and `[[-2],[1],[2],[1]]`.
• What is each quaternion's length?
• What is their quaternionic product?
• Represent a rotation by `pi/2` about `(1,1,1)` as a quaternion.
• Post your solutions to the Feb 20 In-Class Exercise Thread.

Pauli matrices

• We can exponentiate matrices by plugging them into the Taylor series for `e^x := sum_(n=0)^(infty) x^n/(n!)`.
• One of the ways of showing `e^(i theta) = cos theta + i sin theta` is by using the Taylor series for `e^(i theta)`, `cos theta = 1 - x^2/(2!) + x^4/(4!) + cdots`, and `sin theta = x - x^3/(3!) + x^5/(5!) + cdots`
• Pauli in the 1940s, while trying to modify the Schrodinger equation to work for the electron, re-invented the quaternions. In his notation, we imagine a quaternions `[w, x, y, z]^t` as being the complex matrix given by summing:
  `w[[1,0],[0,1]] + i x[[1,0],[0, -1]] + i y[[0,-i],[i,0]] + i z[[0,1],[1,0]]`
• One can verify that the matrix one gets multiplying two quaternions represented as above behaves as our quaternionic multiplication of the last slide.
• Moreover, if we take a unit quaternion `u = [w, hat bb c ]` let `theta = sqrt(c_x^2 +c_y^2 +c_z^2)` be the length of the pure part, and let `bb hat k = 1/theta hat bb c`,
• Then if we plug the matrix for `[0, bb hat c]^t` into the Taylor expansions, `e^([0, bb hat c]^t/2) = cos (theta/2) + sin (theta/2)bb hat k` where `w = cos (theta/2)`. So `u = e^([0, bb hat c]^t/2)`.
• So it makes sense to write unit quaternions as `[[cos(theta/2)],[sin(theta/2)hat bb k]]`.

Rotations with quaternions

Claim. Let `bb hat u` be a direction in `RR^3`, let `theta` be an angle, let `q = [[cos(theta/2)],[sin(theta/2)hat bb u]]`. Let `bb v` be any coordinate vector in `RR^3` written as pure quaternion. Let `R_(theta, bb hat u)` denote a rotation by angle `theta` about `bb hat u`. Set `bb w = R_(theta, bb hat u) bb v`. Then:
`q bb{v} q^(-1) = bb{w}`.

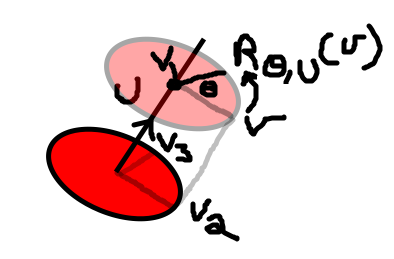
Proof. Given `bb v` let `bb v_1` denote the projection of `bb v` along `hat bb u` and let `bb v_2` denote the portion of `bb v` perpendicular to `hat bb u`. Finally, let `bb v_3 = bb v_1 times bb v_2` complete our coordinate system be the direction we are turning with `R_(theta, bb hat u)`. Note the map `bb v mapsto q bb{v} q^(-1)` is linear so
`q bb{v} q^(-1) = q bb{v_1} q^(-1) + q bb{v_2} q^(-1) = ||bb v_1||q hat bb{u} q^(-1) + q bb{v_2} q^(-1)`. So it suffices to show:

1. `q hat bb{u} q^(-1) = hat bb u`. The axis of rotation is unchanged.
2. `q bb{v_2} q^(-1) = R_(theta, hat bb u) bb v_2` for `bb v_2` perpendicular to `bb u`.

To see (1), let c and s denote the sine and cosine of `theta/2` notice:
`q hat bb{u} q^(-1) = [c, s hat bb u]^t[0, hat bb u]^tq^(-1)`
`= ([0 - s hat bb u cdot hat bb u, c hat bb u + s hat bb u times hat bb u]^t)q^(-1)`
`=( [-s, c hat bb u]^t)q^(-1)`. Notice multiplying the first `q` rotates `[0, hat bb u]` so not pure, multiplying by `q^(-1)` will reverse this.
`=( [-s, c hat bb u]^t)( [c, -s hat bb u]^t)`, using def for inverse from last day.
`=[-cs + cs hat bb u cdot hat bb u, s^2 hat bb u + c^2 hat bb u - cs hat bb u times hat bb u]^t`
`=[-cs + cs, (s^2 + c^2)hat bb u]^t`
`=[0, hat bb u]^t = hat bb u` as desired (we are abusing notation, identifying `[0, hat bb u]^t` with `hat bb u`).

For (2), a similar direct computation is done. We first multiply `q bb{v_2}` to get `[0, c bb v_2 + s bb v_3]^t`. Notice for the multiplying by `q` for this component only performs half of the rotation we want in the desire direction. Multiplying by `q^(-1)` will rotate the rest of the way. It is when we multiply this by `q^(-1)` that we make use of our angle formulas `cos theta = c^2 -s^2` and `sin theta = 2cs` to get that `q bb{v_2} q^(-1) = R_(theta, hat bb u) bb v_2`.

Powering

• Given a unit quaternion representing a rotation. We can determine a `hat bb k` via normalizing the last three entries of the quaternion. Then we can determine `theta` using arctangent. This will give a unique `theta/2 in [-pi, pi]` and so a unique `theta in [-2pi, 2pi]`.
• As,
  `[[cos(theta/2)],[sin(theta/2)hat bb k]] = e^([0, hat bb c]^t/2)`
• It makes sense that we could power the exponential via:
  `(e^([0, hat bb c]^t/2))^alpha = e^([0, alpha hat bb c]^t/2)`,
  a nice Taylor series of matrices.
• If one works out how this affects the quaternion one gets one finds:
  `[[cos(theta/2)],[sin(theta/2)hat bb k]]^alpha = [[ cos((alpha theta)/2)],[sin((alpha theta)/2)hat bb k]]`
• As `alpha` goes from `0` to `1`, we get a series of angles between `0` and `theta`.
• If `cos(theta/2) > 0` we get `theta/2 in [-pi/2, .. pi/2]` and so `theta in [-pi, pi]`. So we can use `alpha in [0,1]` to interpolate the short way between orientations.
• If `cos(theta/2) < 0 ` then `|theta| in [pi, 2pi]` and we will interpolate the long way which is somewhat unnatural. Because of this, in this situation where the first coordinate of the quaternion is negative, we will negate the quaternion before applying the power operation.

Slerping

• Suppose we want to interpolate between two rotations `R_0` and `R_1`.
• Notice first a linear combination of the two matrices `R_0` and `R_1`, say `alpha R_0 + (1 - alpha) R_1` is not usually a rotation, so we don't wan to interpolate this way.
• On the other hand, suppose these two matrices correspond to the quaternions:
  `[[cos(theta_0/2)],[sin(theta_0/2)hat bb k_0]]`, `[[cos(theta_1/2)],[sin(theta_1/2)hat bb k_1]]`.
• Then to do interpolation we just need to compute:
  `([[cos(theta_1/2)],[sin(theta_1/2)hat bb k_0]] [[cos(theta_0/2)],[sin(theta_0/2)hat bb k_1]]^(-1))^alpha [[cos(theta_0/2)],[sin(theta_0/2)hat bb k_0]]`.
• This is often called spherical linear interpolation or slerping.
• Unit norm quaternions are simply points on the unit sphere in `RR^4`. When we do interpolation as above, we are simply moving along the great arc connecting these two quaternions on that sphere.