Introduction

On Monday, we gave an algorithm for first order theorem proving: (1) Prenexify the negation of formula (move quantifiers `forall` and `exists` to front of formula) to prove and as well all formulas in knowledge base, (2) Herbrandize the formula (replace `forall exists` blocks with new function symbols) to get rid of quantifiers, (3) drop remaining `forall` block and convert resulting formula with no quantifiers to CNF, (4) make clauses and use resolution algorithm such as DPLL together with unification algorithm to try to find a refutation.
The last topic we covered Monday was unification, the process of trying to a substitution for the variables in two atomic formulas to make them the same formula. For example, `A(t(f(x_1),y_1), z_2)` and `A(x_2, g(y_2))` can be made the same under the substition `{x_2 |-> t(f(x_1), y_1), z_2 |-> g(y_2)}`
We will give an example of this algorithm in action in a moment.
Before we do, we return to look at Prolog, this time in the first order setting. As in the propositional setting Prolog's restriction to consider only Horn formulas will make the process of goal (proof) finding much more efficient...

Prolog Example

Prolog uses unification. Consider the Prolog program:

num(0).
num(s(X)) :- num(X).

Prolog is case sensitive. Variables must begin with a capital letter, otherwise, Prolog assumes one is referring to a constant or function symbol.

Notice in the above, the clauses now involve first-order, atomic formulas, this is the setting in which most people write their Prolog programs.

From the Prolog prompt we can then do a query like:

|?- num(Y).

It will unify Y with 0 initially and say

Y = 0

To indicate that num(Y) can be made true if we set Y = 0. If we type `n`, we are indicating we don't want that solution and it will try to resatisfying the statement with a different substitution. i.e., it is as if we did the query num(Y), not(Y = 0). To this Prolog, will now make use of the second rule and return:

Y = s(0)

If Prolog did occurs checks then the following kind of query would fail:

|?- num(s (s (X)))

Example of Unify's Execution

Let's return to the unification algorithm from the end of last day. As an example of unify in action, consider:

x' = g(h(x, y), z)
y' = g(w, t(v))

Initially, S, the substitution list is (). Since x' and y' are both terms, we return

Unify((h(x, y), z), (w, t(v)), Unify(g(a, b), g(a, b), ()))

Notice that a, b are new variable names. The second Unify will return S = (), since both g(a, b) are the same thing.

So now we try to unify two lists (h(x, y), z), (w, t(v)).

So we will do Unify( (z), (t(v)), Unify (h(x, y), w, S)). S is still ().

Now we call Unify-var (w, h(x,y), S).

This statement will return (w |-> h(x, y)). We now need to unify (z) and (t(v)) with respect to the substitution (w |-> h(x,y)). When we get the final recursive answer, we will have ( (z |-> t(v)), (w |-> h(x,y)) )

Example of Theorem Proving Process

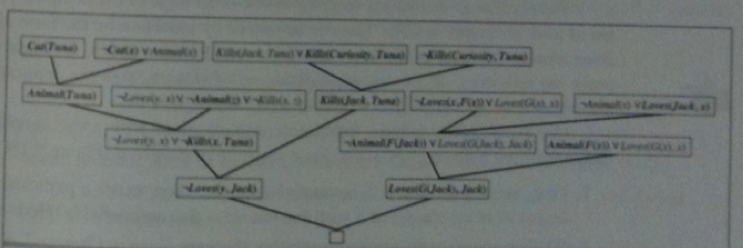
The example images below show going from an English riddle to first-order logic formulas expressing that riddle then Skolemizing and converting to clauses for `KB ^^ neg alpha`, then giving a resolution refutation:

In-Class Exercise

For the example of the last slide, work out how the formula A before the two clauses A1 and A2.
Show how the unification algorithm would unify clause E and F so that resolution could be applied.
Post your solution to the Nov 9 In-Class Exercise Thread.

Equality

So many knowledge bases make use of an equality predicate, `=`, that people have studied this predicate and how to handle it in detail.
One simple approach that people had before people tried to do theorem proving was to just add equality axioms to the knowledge base:
`(forall x) x = x`
`(forall x, y) x = y => y = x`
For any predicate symbol `P`, and substitution slot in this symbol:
`(forall x, y) (x=y ^^ P(..., x, ...)) => P(..., y, ...)`
For any function symbol `f` and substitution slot in this symbol:
`(forall x, y) x=y => f(..., x, ...) = f(..., y, ...).`
The above approach can entail adding lots of axioms to our knowledge base.
For theorem proving, it is often more convenient to add fixed and simple rules of inference which have an equivalent effect. For resolution systems, one rule that works is:
For any terms `r, s, t` where `t` appears somewhere in literal `M_i`, and where `r` and `t` can be unified via `theta`:
`(L_1 vv ...vv L_k vv r=s, qquad M_1 vv ...vv M_n)/(SUB(SUBST(theta, r), SUBST(theta, s), SUBST(theta, L_1 vv ...vv L_k vv M_1 vv ...vv M_n)).`
The above inference is called paramodulation, the special case without `L_i`'s is called demodulation.
An example use of this inference is if `theta = {x mapsto A, y mapsto B}`, then:
`(R(y) vv F(A,y)=y, qquad P(F(x,B),x) vv Q(x))/(R(B) vv P(B,A) vv Q(A))`