Pipeline Architecture

A pipe is a message queue. A message can be anything. A filter is a process, thread, or other component that perpetually reads messages from an input pipe, one at a time, processes each message, then writes the result to an output pipe. Thus, it is possible to form pipelines of filters connected by pipes:

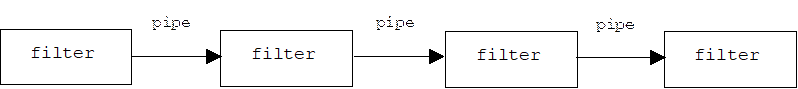
The inspiration for pipeline architectures probably comes from signal processing. In this context a pipe is a communication channel carrying a signal (message), and filters are signal processing components such as amplifiers, noise filters, receivers, and transmitters. Pipelines architectures appear in many software contexts. (They appear in hardware contexts, too. For example, many processors use pipeline architectures.) UNIX and DOS command shell users create pipelines by connecting the standard output of one program (i.e., cout) to the standard input of another (i.e., cin):

% cat inFile | grep pattern | sort > outFile

In this case pipes (i.e.,  "|") are inter process communication channels provided by the operating system, and filters are any programs that read messages from standard input, and write their results to standard output.

LISP programmers can represent pipes by lists and filters by list processing procedures. Pipelines are built using procedural composition. For example, assume the following LISP procedures are defined[1]. In each case the nums parameter represents a list of integers:

// = list got by removing even numbers from nums
(define (filterEvens nums) ... )

// = list got by squaring each n in nums
(define (mapSquare nums) ... )

// = sum of all n in nums
(define (sum nums) ... )

We can use these procedures to build a pipeline that sums the squares of odd integers:

Here's the corresponding LISP definition:

// = sum of squares of odd n in nums
(define (sumOddSquares nums)
   (sum (mapSquare (filterEvens nums))))

Pipelines have also been used to implement compilers. Each stage of compilation is a filter:

The scanner reads a stream of characters from a source code file and produces a stream of tokens. A parser reads a stream of tokens and produces a stream of parse trees. A translator reads a stream of parse trees and produces a stream of assembly language instructions. We can insert new filters into the pipeline such as optimizers and type checkers, or we can replace existing filters with improved versions.

There's even a pipeline design pattern:

Pipes and Filters [POSA]

Other Names

Pipelines

Problem

The steps of a system that processes streams of data must be reusable, re orderable, replaceable, and/or independently developed.

Solution

Implement the system as a pipeline. Steps are implemented as objects called filters. Filters receive inputs from, and write outputs to streams called pipes. A filter knows the identity of its input and output pipes, but not its neighboring filters.

Filter Classification

There are four types of filters: producers, consumers, transformers, and testers. A producer is a producer of messages. It has no input pipe. It generates a message into its output pipe. A consumer is a consumer of messages. It has no output pipe. It eats messages taken from its input pipe. A transformer reads a message from its input pipe, modulates it, then writes the result to its output pipe. (This is what DOS and UNIX programmers call filters.) A tester reads a message from its input pipe, then tests it. If the message passes the test, it is written, unaltered, to the output pipe; otherwise, it is discarded. (This is what signal processing engineers call filters).

Filters can also be classified as active or passive. An active filter has a control loop that runs in its own process or thread. It perpetually reads messages from its input pipe, processes them, then writes the results to its output pipe. An active filter needs to be derived from a thread class provided by the operating system:

class Filter extends Thread { ... }

An active filter has a control loop function. Here's a simplified version that assumes the filter is a transformer:

void controlLoop()
{
   while(true)
   {
      Message val = inPipe.read();
      val = transform(val); // do something to val
      outPipe.write(val);
   }
}

When activated, a passive filter reads a single message from its input pipe, processes it, then writes the result to its output pipe:

void activate()
{
   Message val = inPipe.read();
   val = transform(val); // do something to val
   outPipe.write(val);
}

There are two types of passive filters. A data-driven filter is activated when another filter writes a message into its input pipe. A demand-driven filter is activated when another filter attempts to read a message from its empty output pipe.

 Dynamic Structure: Data-Driven

Assume a particular data-driven pipeline consists of a producer connected to a transformer, connected to a consumer. The producer writes a message to pipe 1, the transformer reads the message, transforms it, then writes it to pipe 2. The consumer reads the message, then consumes it:

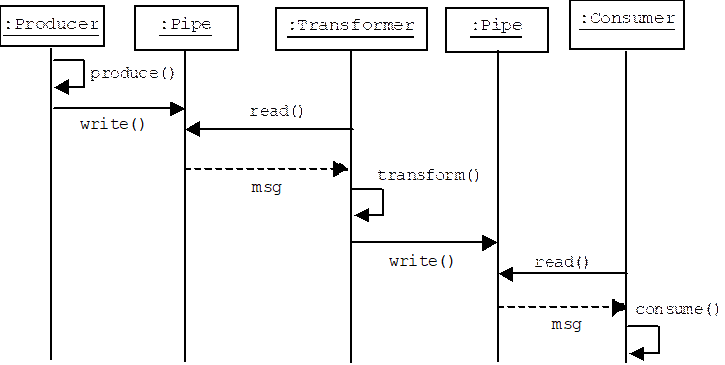
 Dynamic Structure: Demand-Driven

A data-driven pipeline pushes messages through the pipeline. A demand-driven pipeline pulls messages through the pipeline. Imagine the same set up using demand-driven passive filters. This time read operations propagate from the consumer back to the producer. A message is produced and written to pipe 1. The transformer reads the message, transforms it, then writes it to pipe 2. This message is the value returned by the consumer's original call to read():

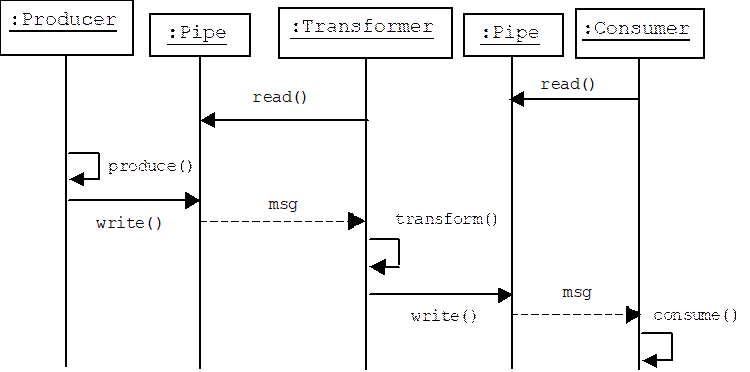
A Problem

Both diagrams reveal a design problem. How does the transformer know when to call pipe1.read()? How does the data-driven consumer know when to call pipe2.read()? How does the demand-driven producer know when to produce a message? Active filters solve this problem by polling their input pipes or blocking when they read from an empty input pipe, but this is only feasible if each filter is running in its own thread or process.

We could have the producer in the data-driven model signal the transformer after it writes a message into pipe 1. The transformer could then signal the consumer after it writes a message into pipe 2. In the demand-driven model the consumer could signal the transformer when it needs data, and the transformer could signal the producer when it needs data. But this solution creates dependencies between neighboring filters. The same transformer couldn't be used in a different pipeline with different neighbors.

Our design problem fits the same pattern as the problem of how the reactor in Chapter 2 communicates with its unknown monitors. We solved that problem by making the reactor a publisher and the monitors subscribers. We can use the publisher-subscriber pattern here, too. Pipes are publishers and filters are subscribers. In the data-driven model filters subscribe to their input pipes. In the demand-driven model filters subscribe to their output pipes.