List Processing in
Scala
Support for processing immutable lists seems to be a tradition in functional programming languages. It began with LISP, which saw symbol manipulation (i.e., processing lists of symbols) as the key to artificial intelligence.
Basic List Stuff
A list is an ordered collection of non-unique elements.
An immutable list can't be modified.
The following session shows some of the basic operations for building and dissecting lists.
scala> val fibs = List(1, 1, 2, 3, 5)
fibs: List[Int] = List(1, 1, 2, 3, 5)
scala> fibs.toSet
res0: scala.collection.immutable.Set[Int] = Set(1, 2, 3, 5)
scala> for(f <- fibs) print(f)
11235
scala> for(i <- 0 until fibs.size) print(fibs(i))
11235
scala> fibs == List(1, 1, 2, 3, 5)
res3: Boolean = true scala> val fibs2 = fibs ++ List(8, 13, 21)
fibs2: List[Int] = List(1, 1, 2, 3, 5, 8, 13, 21)
scala> fibs
res4: List[Int] = List(1, 1, 2, 3, 5)
Notes:
· Fibs contains two 1s. When we convert fibs to a set, one of the 1s disappears. That's because elements in sets must be unique.
· Like all collections, we can traverse lists using a for-loop.
· We access the i-th element of fibs using function call notation: fibs(i).
· List equality is logical (do they have the same elements?) not literal (do they have the same address in memory?).
· Appending elements to a list is non-destructive. I.e., it doesn't change the original list.
scala> fibs2.reverse
res5: List[Int] = List(21, 13, 8, 5, 3, 2, 1, 1)
scala> fibs2.take(3)
res6: List[Int] = List(1, 1, 2)
scala> fibs2.drop(3)
res7: List[Int] = List(3, 5, 8, 13, 21)
scala> fibs2 :+ 34
res8: List[Int] = List(1, 1, 2, 3, 5, 8, 13, 21, 34)
scala> fibs2.contains(7)
res9: Boolean = false
scala> fibs2.indexOf(8)
res10: Int = 5
scala> fibs2.last
res11: Int = 21
List Processing 1.0: head, tail, cons, and Nil
Under the hood all list processing boils down to a few simple operations: head, tail, cons, and Nil. We can think of this as the assembly language level of list processing.
In memory, fibs is a linked list consisting of five cells.
Each cell has two fields: head and tail. The head of a cell contains a list element. The tail contains a pointer to the next cell.
The tail of the last cell contains Nil, the empty list.
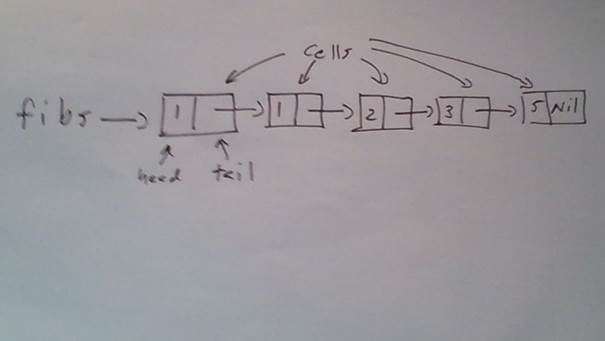
Here's a brief session with cons (::), head, tail, and Nil:
scala> val fibs = 1::1::2::3::5::Nil
fibs: List[Int] = List(1, 1, 2, 3, 5)
scala> fibs.head
res15: Int = 1
scala> fibs.tail
res16: List[Int] = List(1, 2, 3, 5)
scala> fibs.tail.tail.head
res19: Int = 2
List Processing 2.0
There are generally four ways to process a list: iteration, traditional recursion, tail recursion, and pipelines.
List Processing
3.0: Map, filter, and reduce
How would you write a function that filters even numbers from a list of integers?
Easy: if the head of the list is even, cons it onto the result of recursively filtering evens from the tail, otherwise return the result of recursively filtering evens from the tail.
How would you write a function that filters prime numbers from a list of integers?
Easy: if the head of the list is prime, cons it onto the result of recursively filtering primes from the tail, otherwise return the result of recursively filtering primes from the tail.
How would you write a function that filters palindromes from a list of strings?
Easy: if the head of the list is a palindrome, cons it onto the result of recursively filtering palindromes from the tail, otherwise return the result of recursively filtering palindromes from the tail.
Notice that it's nearly the same algorithm. Only the type of list members (Int, String) and the property to be filtered (even, prime, palindrome) is different.
Unfortunately, traditional strong type systems like Pascal's, required programmers to actually write three separate functions.
Fortunately, modern type systems like Scala's allow programmers to write a single function parameterized by both the type of the list members (T) and the property to be filtered:
def filter[T](pred: T=>Boolean, vals: List[T]): List[T] = {
if (vals == Nil) Nil
else if (pred(vals.head))
vals.head::filter(pred, vals.tail)
else filter(pred, vals.tail)
}
Notes:
· How would you implement filter using iteration? Tail recursion?
· The property to be filtered is represented as a Boolean-valued function (sometimes called a predicate):
pred: T=>Boolean // = true if argument has the property
For example, the following predicate detects even numbers:
def isEven(x: Int) = x % 2 == 0;
Here's a sample call to filter:
scala> ages
res24: List[Int] = List(21, 13, 12, 44, 18, 19)
scala> filter(isEven _, ages)
res25: List[Int] = List(12, 44, 18)
scala> ages
res26: List[Int] = List(21, 13, 12, 44, 18, 19)
Notes:
· We pass isEven _ to filter. The underscore tells Scala that isEven is being treated like data rather than being called.
· Notice that filtering elements from a list is non-destructive.
· How would you filter numbers divisible by 3 from a list?
· How would you filter long strings from a list?
Without variables, functional programming lends itself to parallel computing. It's fair to say that the rise of Big Data was made possible by the map-reduce architecture employed by Hadoop and other engines designed to analyze large, unstructured data sets.
Given a unary function, map applies it to each element in a list, returning the list of results. (Of course this is done in parallel in Hadoop.)
The reduce function combines the members of a list into a single value given a binary combiner function.
For example, assume the following declarations have been made:
def avg(nums: List[Double]): Double = {
if (nums.length == 0) throw new
Exception("length = 0")
var sum = 0.0
for(i <- nums) sum += i
sum / nums.length
}
def max(x: Double, y: Double) = if (x < y) y else x
val exam1: List[Double] = List(100, 95, 86, 42)
val exam2: List[Double] = List(35, 73.1, 80, 43.9)
val exam3: List[Double] = List(66, 80, 23.9, 55)
val exams = List(exam1, exam2, exam3)
We can use map and reduce to get the largest average of all of the exams:
scala> exams
res48: List[List[Double]] = List(List(100.0, 95.0, 86.0, 42.0), List(35.0,
73.1, 80.0, 43.9), List(66.0, 80.0, 23.9, 55.0))
scala> exams.map(avg _).reduce(max _)
res49: Double = 80.75
Hey, wait a minute. Does this mean that filter is also built-in? Yup:
scala> ages.filter(isEven _)
res51: List[Int] = List(12, 44, 18)
Problems to contemplate:
· Implement map and reduce using tail recursion.
Stream Processing
A streaming video can be viewed as a potentially infinite sequence of images.
An input device can be viewed as a potentially infinite sequence of characters.
Such sequences can be represented in Scala as streams (now called lazy lists).
Internally, a stream is represented as a linked list of cells representing some prefix of the sequence. However, the tail of the last cell is a promise to compute more cells if they're needed.
For example:
scala> val nums = LazyList(10, 20, 30, 40, 50)
val nums: scala.collection.immutable.LazyList[Int] = LazyList(<not
computed>)
scala> nums.head
val res0: Int = 10
scala> nums
val res1: scala.collection.immutable.LazyList[Int] = LazyList(10, <not
computed>)
scala> nums.tail.head
val res2: Int = 20
scala> nums
val res3: scala.collection.immutable.LazyList[Int] = LazyList(10, 20, <not
computed>)
Notes:
· Nums is a finite stream. Logically, it consists of five elements.
· However, it is implemented as a single cell, Stream(10, ?), where ? represents a promise to compute more cells if needed.
· The tail of this cell is the cell Stream(20, ?), where ? represents a promise to compute still more cells if needed.
· When we re-inspect nums we now see two cells, the ones just computed.
· A promise is a thunk (remember these from lazy evaluation?) A thunk is a frozen function call. In this case the thunk represents the ability to compute the next cell of the stream.
We can define infinite streams by a kind of backwards recursion:
scala> def makeFibs(fib1: Int, fib2: Int): Stream[Int] = fib1
#:: makeFibs(fib2, fib1 + fib2)
makeFibs: (fib1: Int, fib2: Int)LazyList[Int]
scala> val fibs = makeFibs(1, 1)
fibs: Stream[Int] = Stream(1, ?)
Notes:
· makeFibs is a recursive function. It calls itself, but there is no base case. Each call has bigger inputs than the last.
· a #:: b is stream-cons. It creates a cell with head = a and tail = a thunk that will compute b when thawed.
· In other words, the fatal recursive call doesn't happen. Instead, it gets put on ice for later.
Inspecting the fifth element of the stream, fibs(4), executes the recursive call four times. So now the first five elements of the stream have been thawed out:
scala> fibs(4)
res56: Int = 5
scala> fibs
res57: LazyList[Int] = LazyList (1, 1, 2, 3, 5, ?)
They're all there:
scala> fibs(10)
res43: Int = 89
scala> fibs(20)
res45: Int = 10946
scala> fibs(30)
res46: Int = 1346269
scala> fibs(40)
res47: Int = 165580141
scala> fibs(50)
res49: Int = -1109825406
Don't believe me? Try this:
Scala> for(fib <- fibs) print(fib + ", ")
(Save your work, first!)
We can also use map and filter on streams:
scala> val evenFibs = fibs.filter((n: Int)=>n%2 == 0)
evenFibs: scala.collection.immutable. LazyList [Int] = LazyList (2, ?)
scala> evenFibs(5)
res2: Int = 2584
But not reduce. (Why?)