Recursion vs. Iteration

How many bricks does it take to build a staircase of height n?

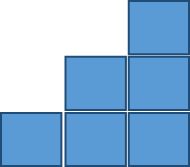
The number of bricks required is called a triangle number because staircases are roughly right triangles.

It should be clear that:

tri(n)
= # of bricks needed to construct a staircase of height n
= 1 + 2 + ... + n

For example:

tri(3) = 1 + 2 + 3 = 6

There are four ways to implement the triangle function.

Classical Recursion

def tri(n: Int): Int = if (n == 0) 0 else n + tri(n - 1)

Note: The return type of recursive functions in Scala must be declared. Why?

Let's trace a call:

tri(4)
4 + tri(3)
4 + 3 + tri(2)
4 + 3 + 2 + tri(1)
4 + 3 + 2 + 1 + tri(0)
4 + 3 + 2 + 1 + 0
4 + 3 + 2 + 1
4 + 3 + 3
4 + 6
10

Note that the trace (called a computation) has length 10 and width 5. These numbers grow in proportion to the size of the input. The length corresponds to the runtime and the width corresponds to the memory needed. Thus the runtime and space complexity of this algorithm in O(n).

Iteration

def tri(n: Int): Int = {
    var result = 0
    for(count <- 0 to n) result = result + count
    result
}

Note that the runtime complexity of this algorithm is still O(n) because we will be required to iterate n times. However, the space complexity is only O(1). Only memory for the variables count and result are needed. These get used over and over again.

Tail Recursion

When a tail recursive function calls itself there are no pending operations that need to be performed on the return value. In other words, the return value of the recursive call is the return value of the function itself. Some compilers and interpreters are optimized to reuse the same stack frame on each recursive call.

For example, the following implementation if tri isn't recursive, but its internal helper function is tail recursive:

def tri(n: Int) = {
   //@tailrec
   def helper(count: Int, result: Int): Int =
      if (n < count) result else helper(count + 1, result + count)
   helper(0, 0)
}

Notes

·       The helper function is imitating the iteration in the previous implementation.

·       Scala automatically optimizes tail recursive functions to reuse stack frames, so strictly speaking, the @tailrec annotation isn't necessary. (In my version of Scala Eclipse it isn't even recognized!) However, if the annotation is used and if the compiler can't perform the optimization—perhaps because the programmer mistakenly believes the implementation is tail recursive, a warning will be issued.

Let's trace a call:

tri(4)
helper(0, 0)
helper(1, 0)
helper(2, 1)
helper(3, 3)
helper(4, 6)
helper(5, 10)
10

Notice that the length of the computation is 8, and the width is 1. Like the iterative solution, the runtime complexity is O(n) but the space complexity is O(1).

Closed Form

Recursive implementations usually arise from the Divide and Conquer strategy, which breaks a problem into simpler sub-problems, solves these recursively, then combines their solutions into the answer of the original problem. In many situations this is the simplest way to solve a problem. (Think of implementing an interpreter or compiler without using recursion!) Finding an iterative solution can be hard, which is why tail recursion is attractive. In languages like Haskell iteration doesn't exist because it requires an implicit or explicit loop control variable, and variables are forbidden.

Finding a closed form solution—requiring neither recursion nor iteration is really difficult. It's analogous to solving a differential equation. At age six Fredrick Gauss realized that:

1 + 2 + 3 + ... + n = (n + 1) + (n – 1 + 2) + (n – 2 + 3) + ... = (n + 1) + (n + 1) + (n + 1) + ... = n * (n + 1)/2

Implementing this formula:

def tri(n: Int) = n * (n + 1) / 2

Note that both the runtime and space complexity of this algorithm is O(1).

Notes:

·       Avoid unnecessary syntax in Scala. Examples include semicolons, curly braces, return statements, and declaring the return type of a function. There is one exception to this last item: you must declare the return type of a recursive function. Why?

·       Practice writing tail recursive functions by first writing an iterative version and then converting the for-loop into a helper function. Make the loop control variable and the result into parameters. (Warning: you many need additional parameters.) Here's a template you can follow:

def tailRecursiveWraper(n: Int) = {
   @tailrec
   def helper(count: Int, result: Int): Int =
      if (n < count) result else helper(count + 1, newResult)
   helper(initCount, initResult)
}

·       In this template you only need to replace newResult and initResult. Typically, initResult and initCount will be 0 or 1 for arithmetic functions. The newResult slot will be filled with some sort of simple function call that computes the new result from count and result:

update(count, result)