NetLogo Review
The following procedures assume the ABS framework is being used to initialize and update turtles and patches.
Random Turtles
Assume a turtle has an attribute called luck:
turtles-own [luck]
Of course some turtles are luckier than others. Luck is randomly distributed through the population. This means that if luck is a number between 0 and 100, then on average the luck of a turtle will be about 50. We can use NetLogo's random number generator to generate random numbers:
to init-turtle
set luck random 101
Let's calculate the average luck for the population:
observer> print mean [luck] of turtles
51.85
Other turtle attributes can also be random:
to init-turtle
set luck random 101
setxy random-xcor random-ycor
; set heading random 360 ; not needed,
heading already random
; set color random 140 ; not needed, color already random
set size 1 + random 3
set shape one-of shapes
end
Here's a screen shot:
Turtle movement can also be random:
to update-turtle
rt random 360
fd random 5
end
Local Knowledge
The behavior of a society can be complex and interesting even though the behavior of the members agents, (turtles and patches) is simple and based on local knowledge. For example, prices can reach equilibrium across many markets even though agents are only aware of prices in nearby markets.
How does a turtle obtain local knowledge?
Assume every turtle has attributes called fitness and vision:
turtles-own [fitness vision]
Vision determines how far a turtle can see (literally or metaphorically). Fitness determines a turtle's health (literal or metaphorical).
Of course not everyone is endowed with the same vision or fitness:
to init-turtle
set vision random 5
set fitness random 101
end
The in-radius Procedure
When a turtle (or a patch) updates itself, it can use the in-radius procedure to collect all of the nearby turtles and patches into sets:
to update-turtle
let turtles-near turtles in-radius vision
The with Procedure
A turtle might like to mate with (fight with, deal with, etc.) nearby turtles that are reasonably fit. A turtle can use the with procedure to filter undesirables from a set of turtles or patches:
to update-turtle
let turtles-near turtles in-radius
vision
let candidates turtles-near with [fitness > 50]
The other Procedure
The updating turtle wants to avoid mating with himself. A turtle can use the other procedure to eliminate itself from the set of candidates:
to update-turtle
let turtles-near turtles in-radius
vision
let candidates turtles-near with
[fitness > 50]
let non-self-candidates other candidates
The one-of Procedure
Any candidate might be a suitable mate (opponent, partner, etc.) A turtle can select a random candidate using the one-of procedure:
to update-turtle
let turtles-near turtles in-radius
vision
let candidates turtles-near with
[fitness > 50]
let non-self-candidates other candidates
let candidate one-of non-self-candidates
Feeling Brave?
You can combine all of the above into a single line if you're brave:
to update-turtle
let candidate one-of other turtles
in-radius vision with [fitness > 50]
The nobody Constant
It's possible that a turtle is isolated and there are no suitable candidates near. Before mating, a turtle should make sure that the selected candidate actually exists. This can be done by comparing the candidate to the nobody constant:
to update-turtle
let candidate one-of other turtles
in-radius vision with [fitness > 50]
if candidate != nobody
[
mate-with
candidate
]
The of Procedure
A turtle can use the hatch procedure to create a new turtle:
hatch 1
[
set vision ???
set fitness ???
]
Suppose the vision and fitness of the offspring should be the averages of the vision and fitness of both parents. We can use the of procedure to report properties of turtles:
to mate-with [mate]
let mother-fitness [fitness] of mate
let mother-vision [vision] of mate
let father-fitness [fitness] of self
let father-vision vision
hatch 1
[
set vision (mother-vision +
father-vision) / 2
set fitness (mother-fitness +
father-fitness) / 2
]
There are two interesting things to note in this procedure. First, the following two constructs are equivalent:
let father-vision [vision] of self
let father-vision vision
This is because self refers to the turtle executing the containing block of instructions, but any unqualified reference to a turtle attribute refers to the attribute of the turtle executing the containing block of instructions.
Second, inside of the hatch block it is the hatchling, not the parent, which executes the instructions. Here vision and fitness refer to the child's vision and fitness.
The myself Constant
If we decided to move the expression [fitness] of self into the hatchling's block, then we would need to change self to myself:
to mate-with [mate]
let mother-fitness [fitness] of mate
let mother-vision [vision] of mate
let father-vision vision
hatch 1
[
set vision (mother-vision + father-vision)
/ 2
set fitness (mother-fitness + [fitness]
of myself) / 2
]
This is because myself refers not to the turtle executing the containing block, but to the turtle that asked the turtle to execute this code.
The ask Procedure
Mating is tiring business. Suppose we end our procedure by decrementing the fitness of each parent. The father (not sure why I decided that the executing turtle was the father, at other times this turtle will be the mother to some other father) simply decrements his fitness, but must ask the mother (i.e., the mate) to decrement her fitness:
to mate-with [mate]
let mother-fitness [fitness] of mate
let mother-vision [vision] of mate
let father-vision vision
hatch 1
[
set vision (mother-vision + father-vision)
/ 2
set fitness (mother-fitness + [fitness]
of myself) / 2
]
set fitness fitness – 10
ask
mate [set fitness fitness - 10]
end
Life
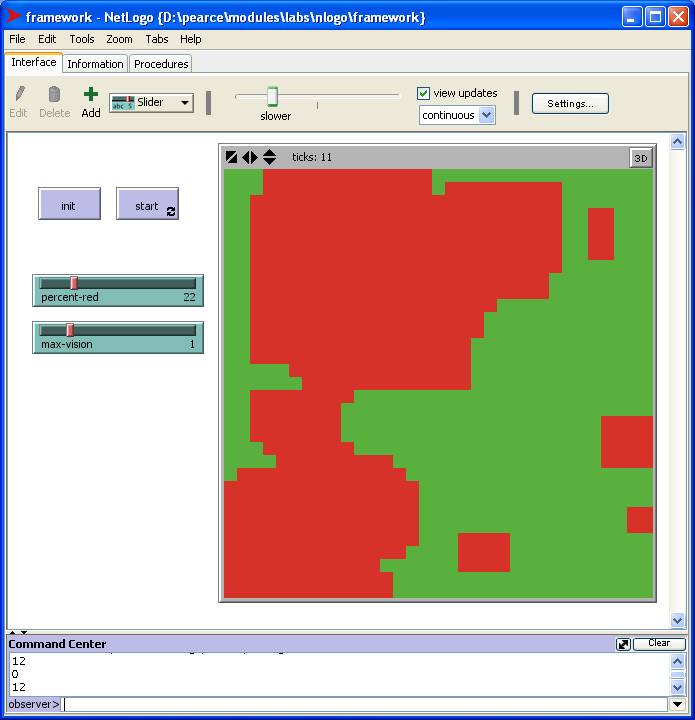
In the game of life a certain percentage of patches are initially red, the rest are green. A patch updates itself by counting the numbers of nearby red and green patches. A patch is nearby if it is within the updating patches range of vision. If the majority of nearby patches are green, then the updating patch turns green, otherwise it turns red.
Allow users to adjust the initial number of red patches as well as the maximum range of vision.
Here's a screen shot:
Death
At the beginning of the game of death 15 turtles have random sizes from 1 to 5. The turtles move around randomly. A turtle picks a random nearby opponent. Each turtle picks a random number less than or equal to its size. The turtle with the largest random number grows in size by one, the other turtle shrinks by one. If a turtle shrinks to size 0, then it dies. The game ends when there is only one turtle left.
Here's a screen shot: