Conway's Game of Life

The Game of Life was invented by British mathematician John Conway and was popularized in Martin Gardner's Mathematical Games column in the October 1970 issue of Scientific American. The Game of Life is not actually a game. It is a powerful computational model that simplifies John Von Neumann's Cellular Automaton (CA) model.

The NetLogo version of Life is derived from BAM, the basic agent model. There are no turtles. Each patch (patches are called cells in a CA) is either alive or dead. This is determined by a Boolean attribute:

patches-own [alive?]

Living patches are white. Dead patches are black.

Initially, the user can use mouse clicks to specify which patches are alive or he can use a slider to specify the percentage of patches that are alive and let the computer randomly decide which patches are alive.

A patch updates itself by first counting the number of neighbors that are alive. NetLogo has three reporters that make this easy:

neighbors = the set of eight neighbors of the active cell

count AGENT-SET = the number of members in AGENT-SET

AGENT-SET with [CONDITION] = the subset of AGENT-SET with CONDITION = true

Here's how we put these together:

to update-patch
let num-living-neighbors count neighbors with [alive?]

Note: If horizontal and vertical wrapping are both turned on, then every cell has exactly eight neighbors.

A living patch dies if it has too few (< 2) or too many living neighbors (> 3). That's okay. A dead patch can be reincarnated if it has exactly three living neighbors.

Here's the code:

life.nlogo

Here's the actual model.

Handling Mouse Clicks

One point of interest in the model is the toggle-alive button. This repeatedly calls the pick-alive procedure, which calls the mouse-down? reporter. This reporter returns true if the mouse button happens to be down and stores the coordinates of the mouse in the pre-defined mouse-xcor and mouse-ycor global variables:

to pick-alive
if mouse-down?
[
ask patch mouse-xcor mouse-ycor
[
ifelse alive?
[
expire
]
[
reincarnate
]
; set was-alive? alive?
]
]
end

Concurrency

The ask command is sequential. In other words, the command:

ask patches [CMMD1 CMMD2 CMMD3]

asks the first patch to execute the entire block of three commands, then the second patch, then the third, etc.

This means that in the above version of Life patches expire or are reincarnated sequentially. However, in Conway's original model patches are updated concurrently. To see how this makes a difference, consider an initial set up in which all patches are dead except a row of three.

All three patches quickly die in the sequential version of Life, but in the concurrent version the middle cell remains alive while its north and south neighbors take turns living and dying with the east and west neighbors:

We can simulate concurrent Life by keeping track of the current and previous state of a patch:

patches-own [alive? was-alive?]

Before any patch updates its alive? attribute, all patches must update their was-alive? attribute:

set was-alive? alive?

One way to achieve this is to make update-patch a two-phase procedure. On even ticks it updates was-alive? on odd ticks it updates alive?

to update-patch
ifelse ticks mod 2 = 0
[
set was-alive? alive?
]
[
; update alive?
]
end

Concurrent ask

NetLogo provides a simulated concurrent version of ask:

ask-concurrent patches [CMMD1 CMMD2 CMMD3]

In this version each patch executes CMMD1. After all patches have executed CMMD1, then each patch executes CMMD2, etc.

Note: This rule only applies to commands that update non-local variables. There are a few other exceptions, too.

We can replace

ask patches [update-patch]

in update-model with:

ask-concurrent patches [set was-alive? alive? update-patches]

Here's the concurrent version:

Generaling the Rules of Life

Every patch can be viewed as a simple two state machine:

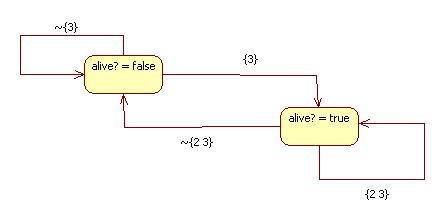
During each cycle a patch transitions from the "alive? = false" state to the "alive? = true" state only if num-living-neighbors is in the set {3}. If it's in the complement of this set: ~{3} = {0 1 2 4 5 6 7 8}, then the patch remains in the "alive? = false" state. If a patch is in the "alive? = true" state, then it transitions to the "alive? = false" state only if num-living-neighbors is in the set ~{2 3} = {0 1 4 5 6 7 8}, otherwise the state remains unchanged.

We can generalize the rules of Life by defining two subsets of the set {0 1 2 3 4 5 6 7 8}. The born-again set contains all of the numbers of living neighbors that cause a patch to change state from "alive? = false" to "alive? = true". The stay-alive set consists of all of the numbers of living neighbors that cause a patch in the "alive? = true" to stay in that state.

Here's a diagram:

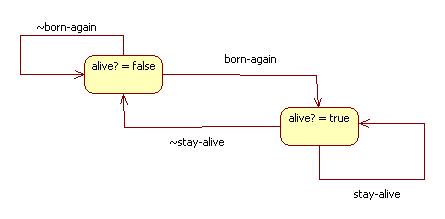
For example, in the standard game of life we have:

born-again = {3}
stay-alive = {2 3}

We denote this rule B3S23.

Here are a few interesting rules:

HighLife = B36S23

Seeds = B2S

Sierpinski = B1S12 (starrt from a single live cell)

Majority = B5678S1234

Try these rules out using the generalized model: