Language Processors
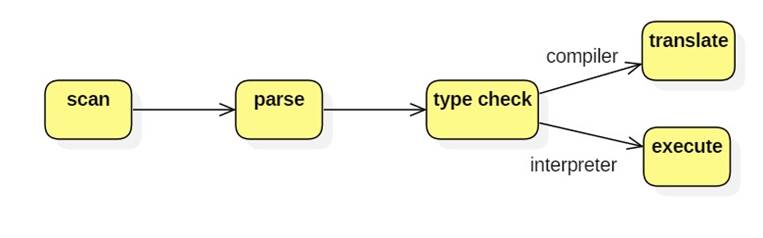
Language processors often use a pipeline architecture, where the output of one processing phase is the input to the next.
The two main types of language processors we are interested
in: are interpreters and compilers. (Other types include assemblers, cross
compilers, and de-compilers.)
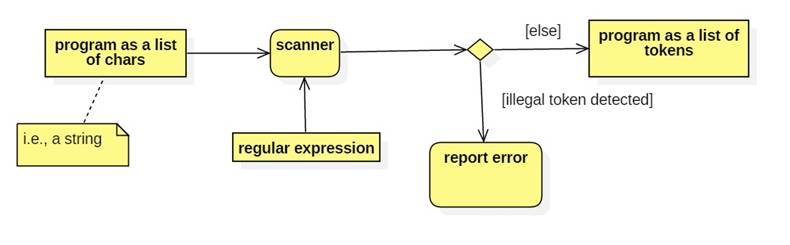
The Scan Phase
Notes:
·
Scanners are similar to spell checkers. They
scan the input program for illegal words or tokens.
· A token is a string that has a meaning or function within a program. Examples of tokens include identifiers (i.e., names like pi, x, and sqrt), literals (numbers, Booleans, chars), operator symbols (+, *, =, etc.) and punctuation symbols (parentheses, semicolons, periods, etc.)
· The set of legal tokens for a language is specified using a regular expression instead of the dictionary a spell checker would use.
· A regular expression is a string that defines a pattern that other strings may or may not match.
Example
The tokens of a language typically include literal values such as integers and doubles.
An integer is a zero or any string of digits that doesn't begin with a zero. Non-zero integers may optionally be preceded by a plus or minus sign.
We can define this pattern in Scala as follows:
scala> val
intPattern = "0|(\\+|-)?[1-9][0-9]*"
intPattern: String = 0|(\+|-)?[1-9][0-9]*
Notes:
| = or
? = optional
* = iterate 0 or more times
[0-9] = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
[1-9][0-9]* = a non-zero digit followed by 0 or more digits
\\+ = literal + (not the regular expression quantifier +, which means iterate 1
or more times)
We can now test various strings to see if they match this pattern:
scala> "123".matches(intPattern)
res4: Boolean = true
scala> "-123".matches(intPattern)
res5: Boolean = true
scala> "+123".matches(intPattern)
res6: Boolean = true
scala> "0123".matches(intPattern)
res7: Boolean = false
The Parse Phase
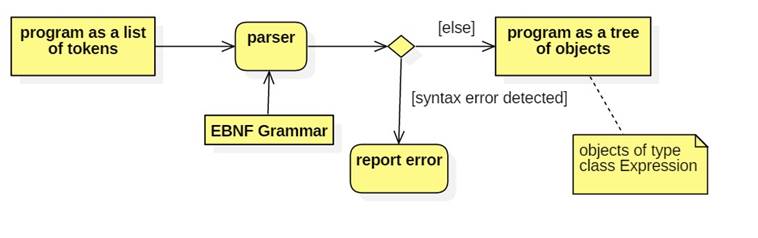
· If scanners are like spell checkers, then parsers are like grammar checkers.
· The parser produces an internal representation of the program in the form of a tree.
· The nodes of the tree (including the root) represent expressions. Child nodes represent sub-expressions of their parent nodes.
Example
The ICalc language allows users to declare names for integers and to call library functions:
-> def x = add(3, 2)
OK
-> mul(x, add(4, 7))
55
First, a class hierarchy of expressions must be defined and implemented:
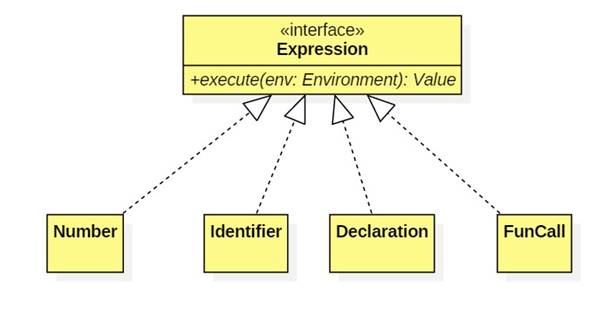
Second, grammar rules must be defined. These specify the structure of grammatically correct expressions:
expression ::= number | declaration | funcall | identifier
number ::= 0|[1-9]~[0-9]*
identifier ::= [a-zA-Z]~[a-zA-Z0-9]*
declaration ::= "def" ~ identifier ~ "=" ~ expression
funcall ::= identifier ~ "(" ~ operands ~ ")"
operands ::= (expression ~ ("," ~ expression)*)?
Often parsers can automatically be generated from these bits of information using tools such as YACC, ANTLR, or Scala's parser combinators.
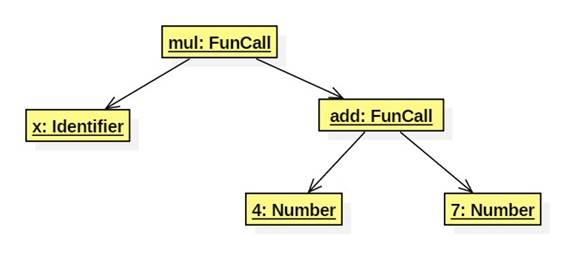
Given the input string "mul(x, add(4, 7))", a scanner might turn it into the token list
["mul", "(", "x", ",", "add", "(", "4", ",", "7", ")", ")"]
The parse would convert this list into the tree:
Notes:
· EBNF = Extended Bachus-Naur Form, this is a type of grammar (similar to context-free grammars) initially developed by Bachus and Naur for Algol60.
· An EBNF grammar rule has the form:
expression-type ::= pattern
· The patterns used in an EBNF grammar are similar to regular expressions. They employ the pattern-generating operations such as |, ?, +, *, and ~ (which means "followed by"). The big difference is that EBNF grammars can use nested recursion. For example, the operands of function calls may themselves be function calls. This is too complex for regular expressions to describe.
The Type Check Phase
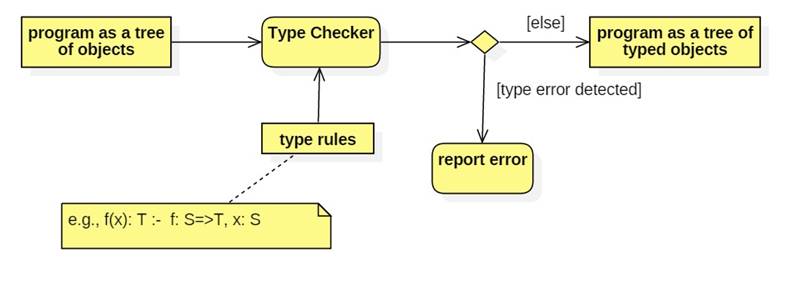
· Starting from the bottom of the expression tree, the type checker associates a type with each node.
·
The type of an expression is the type of the
value it will produce when it is executed. Static type checking figures this
out without executing the expression. Thus, programmers can learn of their type
errors before their program runs.
· One possible type is the failure type, FAIL. If any node in the parse tree has type FAIL, then the root of the tree will also have type FAIL. This indicates that the tree contained a type error.
· Modern type checkers use automated inference to deduce the type of a tree from a set of type rules.
Example
The rule:
f(x): T :- x: S, f: S=>T
asserts that we may infer f(x) is of type T, if we can prove that x is of type S and f is a function of type domain S with range T.
If we have proven that isEven: Int => Boole and that age: Int, then we can use this rule to infer that isEven(age) is of type Boole.
On the other hand, if age: Char, then we must infer that isEven(age): FAIL.
Another Example
Polymorphic type systems include the subsumption rule:
x: S :- x: T, T <: S
This states that x has type S if x has type T and T is a subtype of S. For example, if Rectangle is a subtype of Shape (Rectangle <: Shape), and x is a Rectangle (x: Rectangle), then we can use x in contexts where Shapes are expected. In other words, x also has type Shape (x: Shape).
The Execution Phase
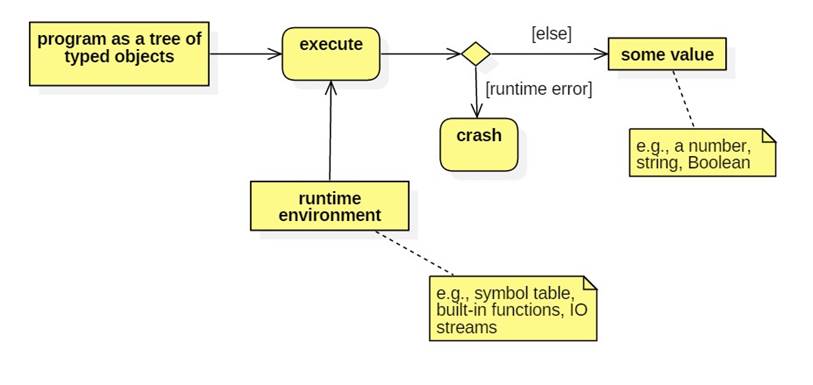
Executing an expression produces a value:
-> mul(x, add(4, 7))
55
We can think of expressions as programmer queries and values as computer-generated answers.
Like expressions, values can be organized into class hierarchies:
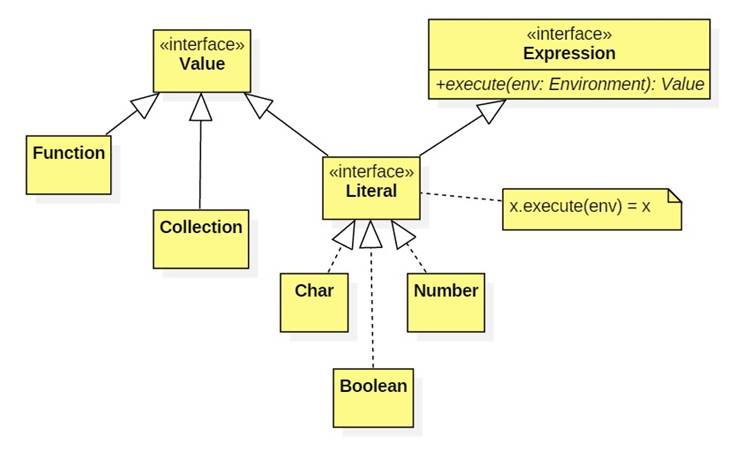
The various implementations of the execute method in the expression subclasses specifies the meaning, behavior, or semantics of the expression.
The Translation Phase
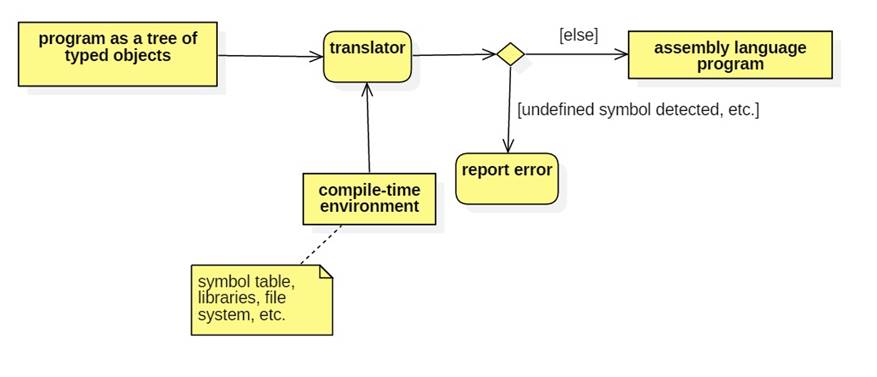
A translator generates an assembly language program from the typed parse tree.
This involves assigning values to memory locations and resolving identifiers that may be used in one part of the program but defined in another.
Example
The expression
mul(x, add(4, 7))
might be translated into a sequence of register machine instructions as:
mov r[0], 4
mov r[1], 7
add r[1], r[0], r[1]
mov r[0], x
mul r[1], r[0], r[1]
Or into a sequence of stack machine instructions as:
push 4
push 7
add
push x
mul
Formal Specification
· Formal Specification of Programming Languages