The Processor

The processor (also called the central processing unit or CPU in case there is just one) is the engine of the computer (and memory the gas tank). Just as a car engine repeatedly moves each piston up and down, the processor repeatedly performs the fetch-execute cycle:

1. fetch next instruction from memory
2. fetch needed data from memory
3. execute instruction
4. store result back in memory
5. goto 1

How many cycles can be completed in a second? Lots, one cycle per second is called a Hertz or Hz. The speed of a Pentium processor is measured in hundreds of megahertz (MHz). One MHz is a million cycles per second!

What types of instructions can a processor execute? Surprisingly simple ones.

Arithmetic

A processor can add, multiply, subtract, and divide integers represented as bit strings. (Byte arithmetic was covered in Bits and Bytes. A processor simply provides a hardware implementation of these algorithms.)

Here's the format of a typical add instruction (though the format may vary among different types of processors).

add X Y

In this instruction X and Y are addresses. The processor executes this instruction as follows:

1. fetch the number stored at memory location X: num1 = memory.read(X)
2. fetch the number stored at memory location Y: num2 = Y or memory.read(Y)
3. add num1 and num2: result = num1 + num2
4. set the carry or overflow flags if necessary
5. store the result back to memory location X: memory.write(X, result)

If we think of an address as a bit string, and if we code operations (add, sub, mul, div, etc.) as bit strings (called opcodes), then the entire instruction can be encoded as a bit string:

Since an instruction is simply a bit string, and since a program is a sequence of instructions, then an entire program—Halo, Linux,, Photoshop—is just a string of bits.

Move

The move instruction allows us to move data around in memory.

move X Y (move data stored at address Y to address X)

A variation allows us to store constants to memory locations:

store X C (store constantc C at address X)

Logic

Sick of philosophical debates turning into shouting matches, Gottfried Leibniz, the co-inventor of calculus (along with Newton), came up with the idea of a reasoning calculus: a mathematical system for determining if propositions were true or false. With it, philosophical debates could be reduced to number crunching:

The only way to rectify our reasonings is to make them as tangible as those of the Mathematicians, so that we can find our error at a glance, and when there are disputes among persons, we can simply say: Let us calculate, without further ado, to see who is right.

Leibniz's dream took a huge step forward a century later when the British mathematician George Boole set aside the definitions of true and false and took them to be arbitrary but distinct values:

true = 1
false = 0

He developed not a calculus of reasoning, but an algebra of reasoning. In this algebra—later called Boolean Algebra-- addition was interpreted as the OR operation, multiplication the AND operation, and negation as the NOT operation.

For example, assume a university admissions office accepts an applicant if he or she is not a felon and is either a good (GPA > 3.0) in-state student or an excellent (GPA > 3.5) out-of-state student. We can represent the admission criterion symbolically as:

F = "Applicant is a felon"

R = "Applicant is a resident"

G = "Applicant is a good student"

E = "Applicant is an excellent student"

Admit = NOT F AND ((R AND G) OR (NOT R AND E))

We can go a step further and represent the admissions criterion as an expression in Boolean Algebra:

Admit = -F * ((R * G) + (-R * E))

Now suppose a particular applicant is not a felon (F = false = 0), is not a resident of the state (R = false = 0), and has a GPA of 3.9 (G = E = true = 1). Substituting in the equation we get:

Admit = -0 * ((0 * 1) + (-0 * 1))

The laws of Boolean Algebra are similar to the laws of regular algebra with a few exceptions. Here are a few:

-0 = 1 and -1 = 0
1 + 1 = 1

Simplifying our formula we get:

Admit = -0 * ((0 * 1) + (-0 * 1)) = 1 * (0 + 1) = 1 * 1 = 1 = true

On other words, the applicant should be admitted.

Boole's algebra might have remained a mathematical curiosity except that it turned out to be the foundation of all of computer science.

To begin, it is very easy to implement the Boolean operations as components made out of a few transistors. These are called logic gates. Here is a circuit representing the admissions criterion:

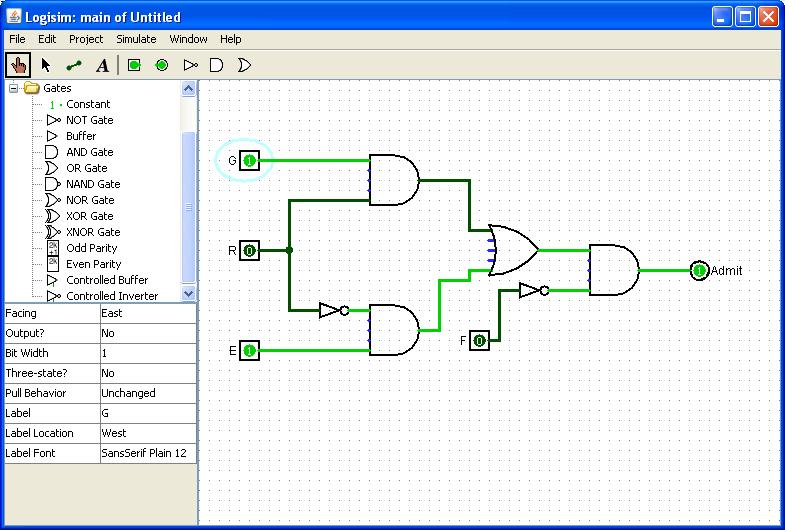
We could use this design to build a microchip that could be used to process applications.

But of course we don't need to build a microchip. All programming languages have instructions for the logical operators AND, OR, and NOT.