Recursive Functions
In Top Down Design functions are implemented in terms of supporting functions, which may or may not exist. Those that do not exist are implemented in terms of their supporting functions, and so on. It seems strange to implement a function using functions that don't exist, but we have faith that eventually these functions will exist.
A bigger test of faith is recursion, in which a function is one of its own supporting functions. This works as long as the calls involve simpler inputs. Here's the general form:
int f(int n)
{
�� if (n == 0)
����� return init;
�� else
����� return combine(n, f(n - 1));
}
where
f(0) = init = the initial or base value
combine(a, b) = any combination of a and b
We can trace the computation generated by calling this function to see why recursion works:
f(3)
combine(3, f(2))
combine(3, combine(2, f(1)))
combine(3, combine(2, combine(1, f(0))))
combine(3, combine(2, combine(1, init)))
combine(3, combine(2, u))
combine(3, v)
w
The base case, f(0) = init, prevents the recursion from an infinite descent into the negative integers.
For example, assume we want to count the number of bricks needed to build a staircase n steps high. This staircase is four steps high and is made out of 10 bricks:
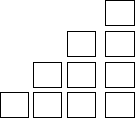
Recursive functions solve recursive problems. A recursive problem is a problem that can be reduced to a simpler problem that's a smaller version of the original problem. For example, notice that we can saw off the last column of our staircase:
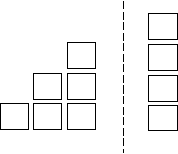
This leaves a column of n bricks plus a staircase that's n - 1 bricks tall. We can compute the number of bricks needed to build the smaller staircase by recursion.
Step I: We begin by naming our function:
bricks(n) = # of bricks needed to build a staircase n steps tall
Step II: Figure out our base case, f(0):
bricks(0) = 0 = # of bricks needed to build a staircase 0 steps tall
Step III: We ask:
How can we compute bricks(n) assuming we can call bricks(n - 1)?
Well, if we saw the last column of bricks off of our staircase, then we can call bricks(n - 1) to get the number of bricks required to build the smaller staircase, then we add the n bricks that we sawed off:
n + bricks(n - 1)
Step IV: Putting it all together we have:
int bricks(n)
{
�� if (n == 0)
����� return 0;
�� else
����� return n + bricks(n - 1);
}
We can trace a few calls to see if and how our recursion works:
bricks(4)
4 + bricks(3)
4 + 3 + bricks(2)
4 + 3 + 2 + bricks(1)
4 + 3 + 2 + 1 + bricks(0)
4 + 3 + 2 + 1 + 0
4 + 3 + 2 + 1
4 + 3 + 3
4 + 6
10
Iterative Solutions
The great advantage of recursion is the powerful recursive assumption we got to make in Step III. Imagine writing a compiler without using recursion. The disadvantage of recursion is inefficiency. Notice that the larger the input, the taller the computation. The taller the computation, the fatter it gets in the middle. The fatter it gets in the middle, the more memory consumed.
An iterative solution, if we can find one, only uses a constant amount of memory, regardless of the size of the input. It usually takes a leap of insight to find an iterative solution. For example, notice that
bricks(n) = 1 + 2 + 3 + ... + n (= n-th triangle number)
This implies we can create an accumulator to compute bricks(n). In general, an accumulator is a loop of the form:
for(int i = 0; i <= n; i++)
�� accum = combine(i, accum);
where initially:
accum = init;
In our case, the new implementation of bricks is:
int bricks(int n)
{
�� int accum = 0;
�� for(int i = 0; i <= n; i++)
����� accum = i + accum;
�� return accum;
}
Closed Solutions
Of course the number of trips through our for loop will depend on the size of the input. It takes time to execute the body of a loop, therefore, the bigger the input, the longer it will take to compute an answer, even if the amount of memory consumed is constant.
If we are very clever and very lucky, we can find a closed solution that involves neither recursion nor iteration. For example, notice that:
1 + 2 + 3 + ... + n = (n + 1) + ((n - 1) + 2) + etc = n * (n + 1)/2
For example:
bricks(4) = 4 * 5 / 2 = 2 * 5 = 10
Here is our closed form solution:
int bricks(int n)
{
�� return n * (n + 1) / 2;
}