Functions: Basic Features

Assume one of many tasks performed by a large program is to display two integers and their average:

int main()
{
task1;
task2;
task3; // display 2 ints & their avg
// etc.
}

Assume the two numbers are stored in integer variables:

int num1 = 15, num2 = 12;

The task is easily implemented by three statements:

cout << "first number = " << num1 << endl;
cout << "second number = " << num2 << endl;
cout << "average = " << (num1 + num2)/2.0 << endl;

(Note that we divide by 2.0, and not 2. Why?)

Each place in the program where this task needs to be performed, we need to repeat these three statements. (We must even re-compute the average, because the values stored in num1 and num2 may have changed.)

int main()
{
int num1 = 15, num2 = 12;
task1;
task2;
task3; // display 2 ints & their avg
// etc.
task62; // display 2 ints & their avg
// etc.
task98; // display 2 ints & their avg
// etc.
}

Our first reaction should be one of relief. It's lucky that the task only requires three statements and not 500! On the other hand, repeating a sequence of statements in several locations throughout a program is considered bad programming practice. For example, what if the task changes slightly. Instead of the average, we must now display the average plus one:

cout << "average + 1 = " << (num1 + num2)/2.0 + 1 << endl;

This is an easy change to make, but how many places do we need to make this change? If we forget to make the change in just one of the many places where this statement occurs, then we have introduced a bug into our program that wasn't there before.

We can formulate this as the Code Replication Avoidance Principle:

Ruthlessly seek out and eliminate replicated code in your programs.

Defining a Function

In C/C++ we can implement tasks as functions. Here's the definition of a function that implements the task of displaying two numbers and their average:

void average()
{
cout << "first number = " << num1 << endl;
cout << "second number = " << num2 << endl;
cout << "average = " << (num1 + num2)/2.0 << endl;
}

The first line of the definition is called the function's signature or prototype:

void average()

The signature tells us the name of the function, the return type, and the parameters. Our function is named "average". The return type is void. This is another way of saying there is no return type. Functions that have no return type are often called procedures. The empty parenthesis is the parameter list. Our function has no parameters. A parameterless function is sometimes called a thunk.

After the signature comes a statement block:

{
cout << "first number = " << num1 << endl;
cout << "second number = " << num2 << endl;
cout << "average = " << (num1 + num2)/2.0 << endl;
}

This block is often called the function block or function body. We think of a function's body as its algorithm. It's important to realize that when a function is defined, its body is not executed. Instead, the body is "put on ice" until needed. Who knows, maybe it will never be needed and we'll save a bunch of time.

Calling a Function

When and where the body of a function needs to be executed, we simply call the function by name:

average(); // display 2 ints & their avg

A function call consists of the name of the function, followed by a list of arguments. The number of arguments corresponds to the number of parameters. Our function has no parameters, hence has no operands. Hence, the operand list is empty. (But we must still show it.)

Each place where the task must be performed in our program can be replaced by a call to our function:

int main()
{
int num1 = 15, num2 = 12;
task1;
task2;
average(); // display 2 ints & their avg
// etc.
average(); // display 2 ints & their avg
// etc.
average(); // display 2 ints & their avg
// etc.
}

We still have code repetition. For example, if the signature of out function should change. For example, suppose we decide to change the name of the function to averagePlusOne, then we must replace each call to the function throughout our program. However, if the body of the function changes. For example, if we display the average plus one, without changing the name of the function, then this change only needs to be made in the definition of the function:

void average()
{
cout << "first number = " << num1 << endl;
cout << "second number = " << num2 << endl;
cout << "average plus one = " << (num1 + num2)/2.0 + 1 << endl;
}

Even more significantly, by separating the definition of a function from the places where it is called, we separate its implementation from its use. This is exactly what the Abstraction Principle recommends. It separates the job of implementing a function-- done in this case by an expert in computing averages-- from using the function-- done perhaps by someone with expertise in user interface design but not in mathematics.

Notice that main is a parameterless function with return type int. If we identify functions with modules, then we can say that main depends on average because main calls average:

Changes to average may force changes to main. In particular, changes to the signature of average will force changes to main, but changes to the body of average shouldn't require changes to main. Since changes to the body are more likely than changes to the signature, we say that main and average are loosely coupled.

Parameters, Operands, and Arguments

We can allow the user of a function some limited ability to customize the function at the point where it is called by adding parameters. To do this, we simply add num1 and num2 to the parameter list:

void average(int num1, int num2)
{
cout << "first number = " << num1 << endl;
cout << "second number = " << num2 << endl;
cout << "average = " << (num1 + num2)/2.0 << endl;
}

When a parameterized function is called, we specify the values of the parameters in the argument list:

average(n1, n2);

In our case the values of the parameters are the variables num1 and num2. Hence:

int main()
{
int num1 = 15, num2 = 12;
task1;
task2;
average(num1, num2); // display 2 ints & their avg
// etc.
average(num1, num2); // display 2 ints & their avg
// etc.
average(num1, num2); // display 2 ints & their avg
// etc.
}

The expressions that appear in the argument list of a function call are called operands. In theory, any integer-valued expression can be an operand. For example, the call:

average(2 + 3, 2 * 2);

produces the output:

first number = 5
second number = 4
average = 4.5

In this example, the operands are the expressions "2 + 3" and "2 * 2". The values of these expressions, 5 and 4, are called the arguments. The parameters of a function can be viewed as temporary variables that are only valid within the body of the function. When a function is called, these temporary variables are created. The arguments are their initial values. When the function terminates, these temporary variables disappear.

In our example, the following temporary variables are declared:

int num1 = 5;
int num2 = 4;

Once inside the body of average, any reference to num1 and num2 are assumed to be references to these temporary variables, and not the local variables num1 and num2 declared by main.

Local Variables, Scope, Extent, and the Function Call Stack

Notice that the parameters of average and the variables of main are both called num1 and num2, respectively. However, the two names do not correspond to the same memory locations.

Internally, each time a function is called, the processor creates a "bundle" of variables called an activation record or stack frame. For example, when the call:

average(2 + 3, 2 * 2);

is executed, the processor creates the activation record:

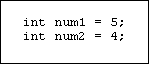
The processor maintains a stack of activation records called the call stack. At the bottom of the stack is main's activation record. The activation record corresponding to the call to average is pushed onto the top of the call stack:

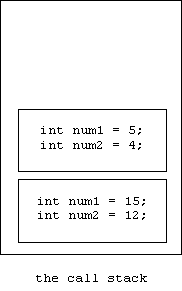
Next, the body of average is executed. When the parameters num1 and num2 are encountered, only the top activation record is searched. When average terminates, its activation record is popped off of the call stack. Now, once again, references to the variables num1 and num2 will refer to the variables declared inside of main.

Local Variables

The body of a function is really an ordinary statement block:

{ <Statement>; <Statement>; <Statement>; etc. }

A declaration is a type of statement. A variable declared inside of a block is called a local variable. Local variables have much in common with parameters. When control enters a block, a new activation record is pushed onto the call stack, and the local variables are placed in it.

For example, let's trace the execution of the following program:

int main()
{
int x = 10;
int y = x + 1;
{
int x = y + 1;
int y = 100;
cout << "x = " << x << endl;
cout << "y = " << y << endl;
}
cout << "x = " << x << endl;
cout << "y = " << y << endl;
return 0;
}

Here's the output produced:

x = 12
y = 100
x = 10
y = 11

Here's what happened. When main was called an activation record was pushed on the stack:

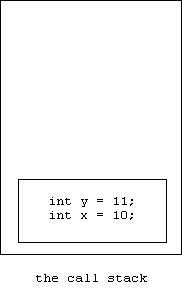
Notice that the value of x was already available to be used to initialize y. Next, control enters the inner block. A new activation record is pushed on the stack:

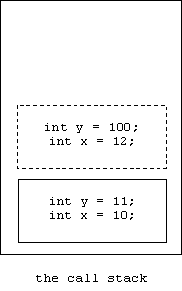
Notice that an activation record for a block is drawn with a dashed border, while the activation record for a function call has a solid border. The reason for this will be explained in the next section.

Also notice that the initial value for x is y + 1 = 11 + 1 = 12. In other words, the inner variable y = 100 hasn't been created yet. The processor drilled down to the next activation record to find a value for y.

Now the following statements are executed:

cout << "x = " << x << endl;
cout << "y = " << y << endl;

The top most activation record is searched for the values of x and y producing the output:

x = 12
y = 100

Upon exiting the block the activation record is popped of the stack. Now when we execute:

cout << "x = " << x << endl;
cout << "y = " << y << endl;

The top-most activation record is searched for the values of x and y producing the output:

x = 10
y = 11

Let's do another example. Assume the following functions have been defined:

int main()
{
int x = 100;
int y = 200;
proc(x + 1, y + 1);
cout << "x = " << x << endl;
cout << "y = " << y << endl;
}

void proc(int a, int b)
{
{
int x = a + a;
int y = b + b;
cout << "x = " << x << endl;
cout << "y = " << y << endl;
}
}

Here's the stack after main is called:

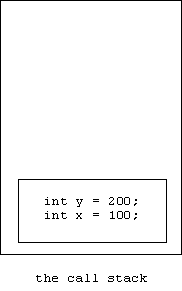
Next proc is called:

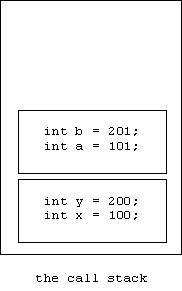
Entering the block inside proc creates another activation record:

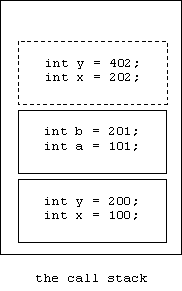
The output statements produce the output:

x = 202
y = 402

After the block is exited, only two activation records are left on the stack. When proc terminates only one activation record is left on the stack. Now the output statements produce the output:

x = 100
y = 200

Scope and Extent

The scope of a variable is the region of the program where it is valid. The visibility of a variable is the region of the program where it is valid. In the first example the scope of y = 11 is the code inside of the box:

The visibility of y = 11 is the scope minus the inner box:

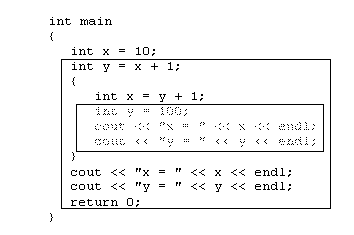
Although y = 11 is valid in the outer box, it's not visible in the inner box because it is shadowed by the variable y = 100.

In general, the scope of a local variable begins at the point of declaration and ends at the end of the block containing the declaration. The visibility of a variable is its scope minus the scopes of any variables with the same name declared in blocks contained within the block.

The extent of a variable is the period of time that the variable exists. For a local variable this is the period from when the variable is in scope.

The Static Scope Rule

Besides the call stack, the processor has three other memory segments available to it:

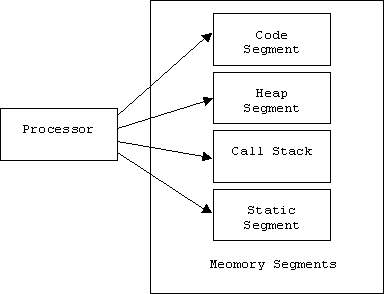
The code segment is where the compiled program resides. Dynamic data structures such as lists and tables reside in the heap segment. Global variables reside in the static segment.

A global variable is a variable that is declared outside of any block. For example, consider the following definitions:

int x = 100;

void proc(int a)
{
cout << "a = " << x << endl;
cout << "x = " << x << endl;
}

int main()
{
int x = 10;
proc(x);
cout << "x = " << x << endl;
return 0;
}

Here's the output produced:

a = 10
x = 100
x = 10

The variable x = 100 is a global variable, while x = 10 is local. Here's what memory looks like as we enter proc:

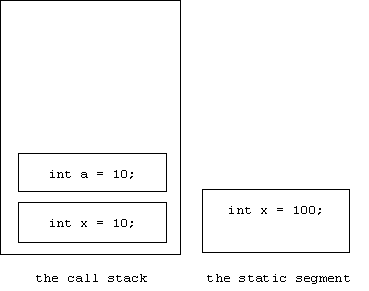
Notice that when proc outputs x, it doesn't drill down to main's activation record. Instead, it searches the static segment for x. This is called the static scope rule.

Let's agree to call activation records created by function calls (e.g., solid borders) statically scoped records, while activation records created by block statements (dashed borders) will be called dynamically scoped records.

To see why it is important to have statically scoped records for functions, consider the following program:

double delta = 1e-10;

bool isSmall(double x)
{
return fabs(x) <= delta;
}

int main()
{
double delta = 100;
double big = 50;
if (isSmall(big))
cerr << "number is too small!"
return 0;
}

Here's what memory looks like as we enter isSmall:

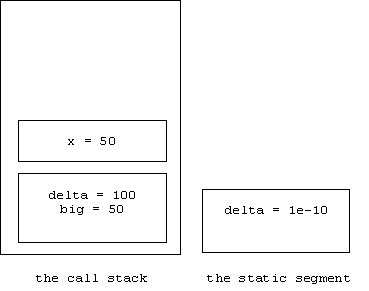
The delta that appears inside of the body of isSmall is called a non-local reference because delta is not contained in isSmall's activation record. If the isSmall record were dynamically scoped, then main's activation record would be searched next, producing the value delta = 100. We end up returning the value of:

50 <= 100

This produces true, probably not the result the user expected.

In general, the creator if isSmall can't anticipate what his caller's activation record will look like. He can only be reasonably expected to know what goes on in his own activation record and the static segment.

Reusability and Return Values

Our average function lacks cohesion. Like the function that computes sales tax and converts temperatures from degrees Fahrenheit to degrees centigrade, average tries to do too much. It computes the average between two numbers and it neatly displays results to the user.

The problem with functions that do too much is that they are difficult to reuse. For example, our average function could only be used by applications that specifically require a function that averages two numbers and displays the result in exactly the way average does.

The Reusability Principle states:

Ideally, modules should be reusable in other applications with little or no modification.

Of course some modules have very narrowly defined purposes that are peculiar to a particular application. The user interface module is a typical example. Such modules have application scope. A module such as a function that computes sales tax has domain scope. We could reuse this function in many business applications, but probably not in scientific or medical applications. A broker is a module that functions as a kind of virtual post office that provides message delivery services to the other modules in a program. Modules of this sort have architectural scope. They can be reused in all applications that use message passing architectures. Trig functions, log and exponent functions, data structures that represent strings, dates, quantities, stacks, etc. have foundation scope. They can be used in almost every type of application. Thus, cohesive modules can be classified into the levels of a hierarchy of decreasing reusability:

Level 4: Foundation Scope
Level 3: Architectural Scope
Level 2: Domain Scope
Level 1: Application Scope

Our average function not only combines two distinct tasks, it makes the situation worse by combining two tasks at opposite ends of our reusability hierarchy: computing the average of two numbers probably belongs to the Foundational level, while displaying the average of two numbers belongs to the Application level. In general, modules at one level of our reusability hierarchy should never depend on modules at lower (hence less reusable) levels. One example of this policy is the Model-View Separation Principle, which states:

Application logic and data should be independent of presentation logic (i.e., code that deals with user input and output).

In some applications the module that encapsulates application logic and data is called the model. If the user interface module encapsulates user input and output, then we can represent the Model-View Separation Principle graphically as two modules with a unidirectional dependency between them:

Applying these principles to our average function, it might be wise to split the function in two: one function computes the average, the other calls the first and displays the result. Here's the second function. We can think of it as part of our "user interface" since it generates output to the user:

void displayAverage(int num1, int num2)
{
cout << "first number = " << num1 << endl;
cout << "second number = " << num2 << endl;
cout << "average = " << average(num1, num2) << endl;
}

Notice that the call to average appears in a position where a number is expected.

A true function, as opposed to a procedure, returns a value to its caller:

double average(int num1, int num2)
{
return (num1 + num2)/2.0;
}