Finite State
Machines
Definitions
Finite state machines (FSMs) are also called finite automata. (At least by me.) Interested readers should consult one of the recommended texts for a more traditional development of automata theory.
A finite state machine M consists of seven components:
M.STATES = a finite set of states
M.FINALS = a subset of STATES
M.start = an element of STATES (the initial state of M)
M.state = an element of STATES (the current state of M)
M.TOKENS = a finite set of symbols
M.transition = a function of type TOKENS X STATES -> STATES
M.accept = a function of type TOKENS* -> boolean
Initially, M.state = M.start. Given a string of tokens, s, M.accept(s) iteratively calls M.transition and updates M.state. If when the end of s is reached M.state is in M.FINALS, then we say M accepts s, otherwise M rejects s.
Here is a pseudocode version of the above description:
boolean accept(TOKENS* s) {
state = start;
for(TOKENS token: s) {
state = transition(token, state);
}
return FINALS.contains(state);
}
Let L(M) = all token strings accepted by M. (So L(M) is a subset of M.TOKENS*.)
FSM Diagrams
Finite state machines can be represented by state machine diagrams in which states are nodes and transitions are arrows labeled by tokens.
For example, here's an FSM that recognizes all strings that match the regular expression 0+1+0+:
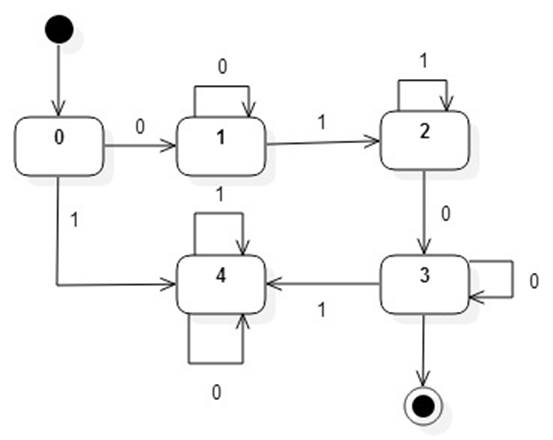
FSM diagrams are closely related to UML statechart diagrams and UML activity diagrams.
Applications
specifying and recognizing tokens
specifying combinational circuits
modeling object lifecycles
specifying protocols
specifying workflows
Enhancements
Fork and join are special transitions. A fork allows multiple states to be active simultaneously. A join waits for multiple source states to transition. Only when all transition is the destination state entered.
A composite state is a state AND an FSM. Entering the composite state enters the initial state of the FSM. If and when the FSM reaches a final state causes the transition out of the composite state.
A completion transition is an unlabeled transition. Entering the source state automatically triggers a transition to the destination state.
In addition to a token, transitions exiting a conditional state may also be labeled by mutually exclusive Boolean-values guard expressions which need to be true to enable the transition.
Theorem An enhanced
FSM can be emulated by an unenhanced FSM.
Proof: In lecture. Note that guard conditions must be severely restricted for this to be true.
Theorem If L = L(r)
for some regular expression r, then L = L(M) for some fsm M.
Proof.
Our proof uses induction on
the depth of nesting of r.
If r is a literal string
(depth = 0) then it's an easy matter to construct a fsm that accepts only r.
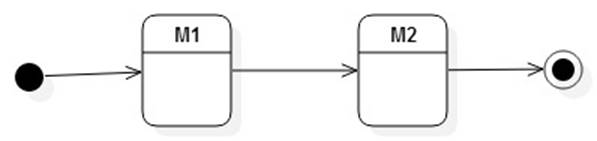
Assume r = st. In this case
the depth of r is more than the depths of s and t. We may thersefore assume by
induction that L(s) = L(M1) and L(t) = L(M2) where M1 and M2 are FSMs. Then L(r)
= L(M) where M is defined as:
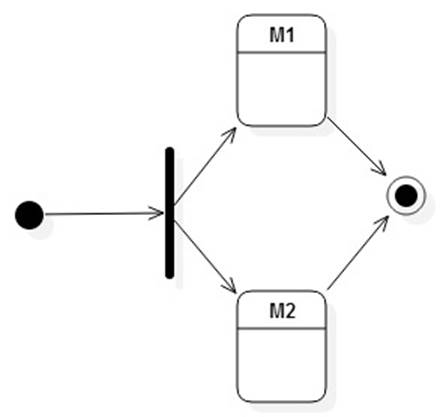
If r = s|t, then L(r) = L(M) where M is defined as:
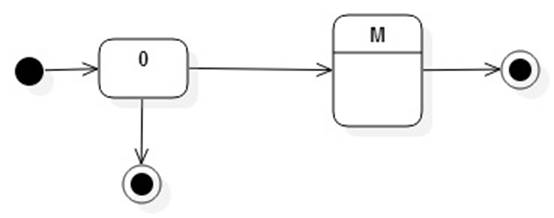
If r = s?, then L(r) = L(M) where M is defined by:
If r = s+, then L(r) = L(M) where M is defined by:
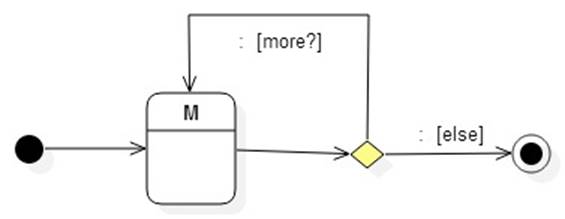
QED.
Theorem If L = L(M) for
some fsm, M, then L = L(r) for some regular expression r.
Proof:
Recall M.transition(c, s) = t means that if m is in state s and the next token is c, then M transitions to state t. We can extend this method to work with strings.
int transitions(String s, int u, int lim) {
int state = u;
for(int i = 0; i < s.length(); i++)
{
state = transition(s.charAt(i),
state);
if (lim < state && i <
s.length – 1) throw new Exception("limit exceeded");,
}
return state;
}
Define R(i, j, k) = {s: String | transitions(s, i, k) = j}.
Claim: R(i, j, k) = R(i, j, k – 1) U R(i, k, k – 1)(R(k, k, k – 1))*R(k, j, k – 1)
Proof of claim: Strings that cause transitions from state i to state j that does not pass through (i.e., enter AND exit) states bigger than k are of two types:
1. Strings that don't cause transitions from i to j that don't pass through states bigger than k – 1, or
2. Strings of the form ab*c where a causes transitions from i to k without transitioning through states bigger than k – 1, followed by a bunch of strings that cause transitions from k to k without passing through states bigger than k – 1, followed by a suffix that transitions from k to j without going through states bigger than k – 1.
Returning to the main proof: We can now show by induction on k that R(i, j, k) = L(r(i, j, k)) where r(i, j, k) is a regular expression. (Left as an exercise.)
L(M) is simply the union of R(0, i, n) where i is a final state and n = the biggest state.
QED.