Context Free Languages

A context-free grammar (CFG) is a set of rules of the form:

VARIABLE ::= PATTERN₁ | PATTERN₂ | ...

This rule says that the variable on the left side of the "consists of" sign (::=) can be replaced by any of the patterns on the right. The patterns are regular expressions that may also contain variables.

For example, the following grammar says that an expression consists of two expressions separated by a + or * operator, and expression surrounded by parentheses, an identifier, or an integer:

EXP ::= EXP \+ EXP | EXP \* EXP | (EXP) | ID | INT
ID ::= [a-zA-Z][0-9a-zA-Z]*
INT ::= [1-9][0-9]*

Derivations

Assume G is a grammar and u and v are strings that may contain variables from G, then a production u => v means that v can be obtained from u by replacing a variable in u with a pattern according to one of the rules in G.

A derivation u =>* v is a sequence of productions: u => u1 => u2 => ... => v.

For example, let G be the EXP grammar above, then the string x + (42 * y) can be derived from EXP (EXP =>* x + (42 * y)). Here's a derivation:

EXP =>
EXP + EXP =>
EXP + (EXP) =>
EXP + (EXP * EXP) =>
ID + (EXP * EXP) =>
x + (EXP * EXP) =>
x + (INT * EXP) =>
x + (42 * EXP) =>
x + (42 * ID) =>
x + (42 * y)

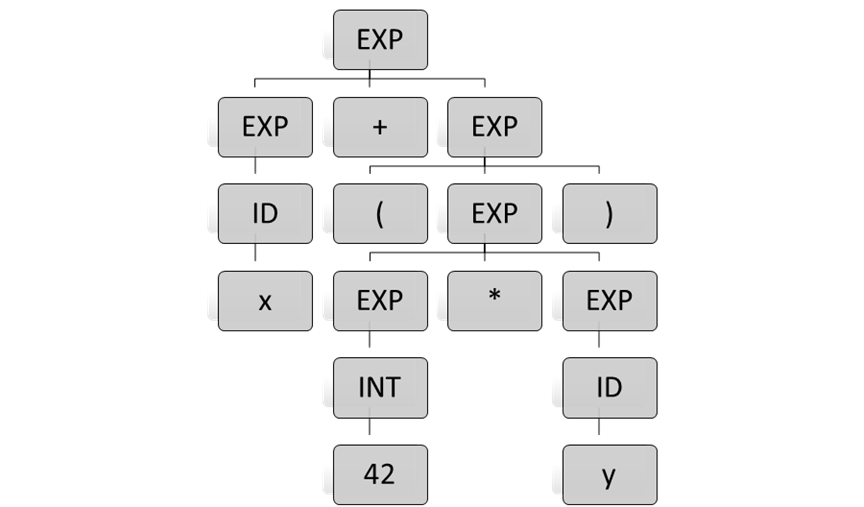
Parse Trees

The parent nodes of a parse tree are labeled by variables. Leaves are variable-free strings. Concatenated, the children of a parent form a pattern. Derivations can be represented as parse trees. For example, here's a tree representation of the previous derivation:

 

Executing and Translating Parse Trees

Recall that a simplified language processor (compiler of interpreter) is a pipeline:

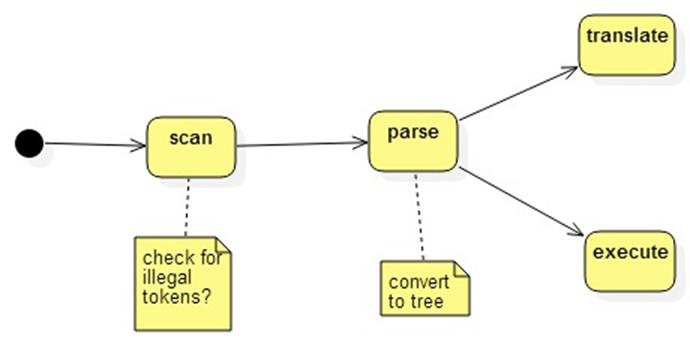
In tree form, it's easy to execute or translate a program using recursion.

CFL

Assume G is a CFG, and assume S is a designated "start" variable.

L(G) = all variable-free strings that can be derived from S
      = {w | S =>* w and w is variable-free}

CFL = the family of context-free grammars = {L | L = L(G) for some CFG G}

Examples

Example 1

S ::= 0S0 | 1

eg. S => 0S0 => 00S00 => 000S000 => 0001000

L(S) = {0ⁿ10ⁿ| 0 < n}

Example 2

BEXP ::= DISJUNCTION

DISJUNCTION ::= CONJUNCTION~(||~DISJUNCTION)?

CONJUNCTION ::= VALUE~(&&~VALUE)*

VALUE ::= true | false | !VALUE