Designing Sequential Circuits

A Mod-2^N counter is a sequential circuit with two inputs: x and clock, and an N bit output called state, which is the same as the internal state.

Internally, there are 2^N states: 0, 1, 2, ..., 2^N – 1

State changes occur on clock pulses according to the formulas:

if (x == 0) state = (state - 1) % 2^N

if (x == 1) state = (state + 1) % 2^N

Counters are useful as clocks that take as input a clock that divides time into two phases: 0 and 1, and splits this time into 2^N phases.

For example, the fetch-execute cycle of a processor may need three phases:

phase 0: IR = cell[PC]
phase 1: PC++
phase 2: execute IR

Each of these phases might be divided into sub-phases.

Building a clocked Mod-4 Counter

In this section we will outline the technique for building a sequential circuit.

Step 1: Derive a state diagram and/or state table

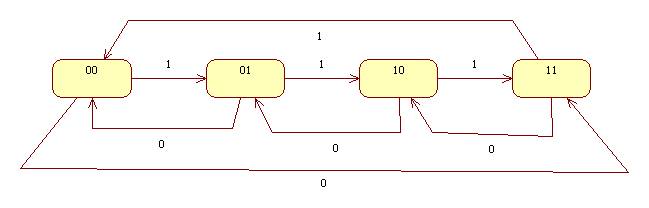
A Mod-4 counter has 4 states:

00, 01, 10, 11

The output of a mod-4 counter is its state.

A mod-4 counter has a 1 bit input, x = 0 or x = 1 and a clock. On a clock pulse the state updates according to the formulas:

if (x == 1) state = (state + 1) % 4
if (x == 0) state = (state - 1) % 4

Here's a state diagram for a Mod-4 counter:

Here's the state table for a mod-4 counter:

current state	x = 0	x = 1
00	11	01
01	00	10
10	01	11
11	10	00

Step 2: Compute p, the number and types of flip-flops needed

If the number of states is n, then:

2^p-1 < n <= 2^p

In out case n = 4 so we will need two S-R flip-flops: F0 and F1.

Call the outputs of F0 Q0 and Q0'. Call the outputs of F1 Q1 and Q1'. Then the state of our circuit will be Q1Q0.

Step 3: Separate the state transition table into p tables, one for each flip-flop

F0

current state	x = 0	x = 1
00	1	1
01	0	0
10	1	1
11	0	0

F1

current state	x = 0	x = 1
00	1	0
01	0	1
10	0	1
11	1	0

Step 4: Derive an input table for each flip-flop

F0

F0 has two inputs: S0 and R0.

current state (Q1Q0)	x = 0	x = 1
00	S0 = 1, R0 = 0	S0 = 1, R0 = 0
01	S0 = 0, R0 = 1	S0 = 0, R0 = 1
10	S0 = 1, R0 = 0	S0 = 1, R0 = 0
11	S0 = 0, R0 = 1	S0 = 0, R0 = 1

F1

F1 has two inputs S1 and R1.

current state	x = 0	x = 1
00	S1 = 1, R1 = 0	S1 = 0, R1 = 0
01	S1 = 0, R1 = 1	S1 = 1, R1 = 0
10	S1 = 0, R1 = 1	S1 = 1, R1 = 0
11	S1 = 1, R1 = 0	S1 = 0, R1 = 1

Step 5: Derive an input equation for each flip-flop and the circuit output equations

F0

S0 = !Q0

R0 = Q0

F1

S1 = !x && !Q0 && !Q1 || x && Q0 && !Q1 || x && !Q0 && Q1 || !x && Q0 && Q1
= !(x || Q0 || Q1) || x && (Q0 xor Q1) || !x && Q0 && Q1

R1 = !x && (Q0 xor Q1) || x && Q0 && Q1

Step 6: Draw the circuit diagram

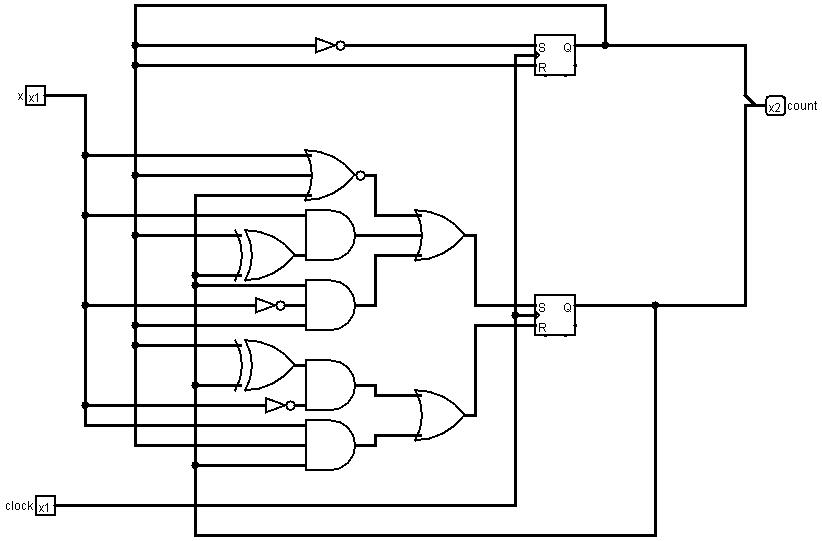
See mod4.circ

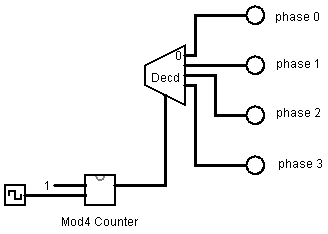
An Application: A four phase clock

Connect a 2-phase clock to the clock input of a mod4 counter and a constant 1 to x. Connect the output to the input of a 2-bit decoder.

Connect the 4 outputs of the decoder to LEDs (from the I/O library.)

Select "Ticks Enabled" from the Simulate menu.