Outline

• S-K Algorithm
• Quiz
• Numpy

Introduction

• Last week, we were looking at the `S-K` algorithm to compute maximal separators for SVMs.
• `S-K`-algorithms get their name from a Schlesinger, Kalmykov, Suchorukov (1981) paper on how to compute `epsilon`-approximation of the maximal separator.
• We said traditional approaches to SVM separator computation are usually based on the so-called sequential minimal optimization (SMO) of a quadratic program; whereas, the `S-K` algorithm approaches are based on computing some kind of convex hull of the positive and negative training examples.
• We considered two convex hull variants `mu`-reduced convex hulls and `lambda`-scaled convex hulls.
• Liu, Liu, Pan, Wang (2009) have shown that separators on scaled convex hulls converge to the soft max margins that would be computed by quadratic programming approach of the original SVM paper of Cortes Vapnik. On the other hand, they are 2-3 times faster to compute.
• Before we present the `S-K` algorithm lets look at some properties of the two types of convex hulls mentioned above...

Some Facts About the Scaled-Convex Hull

• When `lambda = 1`, the scaled convex hull is the usual convex hull.
• The centroid of the scaled convex hull is the same as the original convex hull.
• Given a set `X = {vec(x)_1, ..., vec(x)_k}`, we denote by `X'` the set of points in `S(X,lambda)`, `{vec(x)_i' = lambda vec(x)_i + (1 - lambda) vec{m} | i=1, ..., k}`.
• Let `X^+` and `X^-` be two sets with different centroids, `vec{m}^+ ne vec{m}^-`. Then we can choose `lambda` small enough such that `S(X^+, \lambda)` and `S(X^-, \lambda)` can be separated.
• In particular, in the above, one can show that if `r = || vec{m}^+ - vec{m}^-||`, if `r^+ = max_{vec{x}_i in X^+} ||vec{x}_i - vec{m}^+||`, and if `r^(-) = max_{vec{x}_i in X^-} ||vec{x}_i - vec{m}^-||`, then we can take any value of `lambda` such that `lambda le r/(r^+ + r^-)`.
• Since `r`, `r^+`, and `r^-` are easy to compute, if we are in a situation where the data might not be separable, we can calculate `lambda`, then run our separator algorithm on the points `X^+'` and `X^(-)'`.
• Notice also that to compute `m`, `m^+`, `m^-`, `r`, `r^+`, and `r^-`, we do not anywhere compute the complete convex hulls!! That would be VERY SLOW in higher dimensions.
• The S-K algorithm as we present it relies on the fact that the above procedure ensures the convex hulls of `X^+'` and `X^(-)'` are separable, but does not compute these hulls!

S-K Algorithm - Non-Kernel Version

Suppose our training data is `X = {vec{x}_1, ..., vec{x}_k}`. Let `I = {1, ..., k}`. Let `X^+` be the positive examples, and `I^+` be the indices of the positive examples. Let `X^-` be the negative examples, and `I^-` be the indices of the negative examples. Define `X'`, `X^(+)'`, and `X^(-)'` as per the last slide.

1. Initialization: Set the vector `vec{w}^{+}` to any point `x in X^(+)'` and `vec{w}^{-}` to any point `vec{x} in X^(-)'`. At each step of our algorithm our separator will be given by `vec{w} = vec{w}^{+} - vec{w}^{-}` and `theta = (||vec{w}^{+}||^2 - ||vec{w}^{-}||^2)/2`. To understand what these weights mean consider the two parallel hyperplanes, given by `vec{n}\cdot (vec{x} - vec{w}^{-}) = 0` and `-vec{n}\cdot (vec{x} - vec{w}^{+}) = 0` where `vec{n} = (vec{w}^{+} - vec{w}^{-})/(||vec{w}^{+} - vec{w}^{-}||`. These two hyperplanes are `||vec{w}|| = ||vec{w}^{+} - vec{w}^{-}||` apart. A point half-way between these hyperplanes is given by `(vec{w}^{+} + vec{w}^{-})/2`. Projecting this along the vector `vec{w} = vec{w}^{+} - vec{w}^{-}` which points between the hyperplanes, gives us `((vec{w}^{+} - vec{w}^{-}) \cdot (vec{w}^{+} + vec{w}^{-}))/2 = (||vec{w}^{+}||^2 - ||vec{w}^{-}||^2)/2 = theta`.
2. Stop Condition: Find the vector `vec{x}'_t in X'` closest to either of our current hyperplanes. To do this we choose `t = mbox(argmin)_{i in I} m(vec{x}'_i)` where `m(vec{x}'_i)` is `vec{n}\cdot(vec{x}'_i -vec{w}^{-})` for `i in I^+` and is `-vec{n}\cdot (vec{x}'_i -vec{w}^{+})` for `i in I^-`. The sign of `m(vec{x}'_t)` indicates which side of hyperplane on. For the hyperplane to classify the corresponding data correctly, we want the sign to be positive, however, we'll be satisified if the sign is only slightly negative. More precisely, if `||vec{w}^{+} - vec{w}^{-}|| - m(vec{x}'_t) < epsilon`, stop output `vec{w}` and `theta` given by the formulas above.
3. Adaptation: If `vec{x}'_t in X^+'`, set `vec{w}^{-} := vec{w}^{-}` and set `vec{w}^{+} := (1-q) vec{w}^{+} + q vec{x}'_t` where `q = min(1, ((vec{x}'_t -vec{w}^{-})\cdot(vec{w}^{+} - vec{w}^{-}))/(||vec{w}^{+} - vec{w}^{-}||^2))`; otherwise, set `vec{w}^{+} := vec{w}^{+}` and set `vec{w}^{-} := (1-q) vec{w}^{-} + q vec{x}'_t` where `q = min(1, ((vec{x}'_t -vec{w}^{+})\cdot(vec{w}^{-} - vec{w}^{+}))/(||vec{w}^{+} - vec{w}^{-}||^2))`.

S-K Algorithm - Intuitions

• At any step in the algorithm `vec{w}^{+}` is a linear combination of elements in `X^+'` and `vec{w}^{-}` is a linear combination of elements in `X^(-)'`.
• So as `X^+'` and `X^-'` are separable `||vec{w}^{+} - vec{w}^{-}||` is always greater than or equal to some minimal distance between these sets.
• So if `m` is within distance `epsilon` of being on the correct side of its hyperplane and at the minimal needed distance, we stop.
• Otherwise, we adjust `vec{w}^{\pm}`'s so as to make `vec{x}'_t` more close to being on the correct side of its hyperplane, by making `vec{x}'_t` a support vector and `vec{w}^{\pm}` a linear combination of `vec{x}'_t` and the existing vectors. Notice if we are way off, we'll get `q=1` and we set `vec{w}^{\pm} = vec{x}'_t` to do this.
• The proof of correctness of this step is given in Franc and Hlavac and is similar to the proof of perceptron convergence, we have a potential function (the current `||vec{w}^{+} - vec{w}^{-}||`) which is always decreasing by a constant amount each iteration and which is bounded below by the minimum distance between the convex hulls `conv(X^+)` and `conv(X^-)`.

S-K Algorithm - Kernel Version - Preliminaries

• We now replace dot products in the previous algorithm with the use of kernels...
• Suppose our training data is `X = {vec{x}_1, ..., vec{x}_k}`. Let `I = {1, ..., k}`. Let `X^+` be the positive examples, and `I^+` be the indices of the positive examples. Let `X^-` be the negative examples, and `I^-` be the indices of the negative examples. Let `y_i = 1` if `x_i in X^+` and `y_i = -1` otherwise. Define `X'`, `X^(+)'`, and `X^(-)'` as per two slides ago.
• Let `delta_{i,t}` be 1 if `i = t` and 0 otherwise.
• If `K(vec{x}, vec{x}')` is the kernel function we are using, our final SVM will compute `g(vec{x}) = sign(sum_{i in I} alpha_i y_i K(vec{x}, vec{x}'_i) + (B - A)/2)`. Here `alpha_i in RR` will typically be 0 except for a small number of `i`'s, `A, B in RR` are constants we will define in a moment.
• If we imagine that the non-linear map that the SVM is supposed to compute before apply a perceptron gate is: `vec{f}:RR^n -> RR^m`. Then the kernel `K(vec{x}, vec{z})` is supposed to replace `vec{f}(vec{x})cdot f(vec{z})`. `alpha_i`'s in `g` will be nonzero in the above only if `vec{f}(vec{x}'_i)` is a support vector.
• If in the non-kernel version of the algorithm we need to compute an expression like: `(vec{x}'_t -vec{w}^{-})\cdot(vec{w}^{+} - vec{w}^{-})` to make a kernel version we will first expand this as `vec{x}'_t\cdot vec{w}^{+} - vec{x}'_t\cdot vec{w}^{-} - vec{w}^{-}\cdot vec{w}^{+} + vec{w}^{-}\cdot vec{w}^{-}`. Roughly, the kernel can be applied to each term in the expression: `K(vec{x}'_t, vec{w}^{+}) - K(vec{x}'_t, vec{w}^{-}) - K(vec{w}^{-}, vec{w}^{+}) + K(vec{w}^{-}, vec{w}^{-})` to get the kernelized analog.

S-K Algorithm - Kernel Version

Algorithm:

1. Initialization: Set `alpha_(i_1) = 1` for `i_1 in I^+`, `alpha_(j_1) =1` for `j_1 in I^-`. Set all the remaining `alpha_i = 0`. Set `A = K(vec{x}'_{i_1}, vec{x}'_{i_1})`, `B = K(vec{x}'_{j_1}, vec{x}'_{j_1})`, `C= K(vec{x}'_{i_1}, vec{x}'_{j_1})`. For `i in I` define `D_i = K(vec{x}'_{i}, vec{x}'_{i_1})` and `E_i = K(vec{x}'_{i}, vec{x}'_{j_1})`.
2. Stop Condition: Find the vector `vec{x}'_t in X'` closest to our current separating hyper-surfaces. To do this we choose `t = mbox(argmin)_{i in I} m_i` where `m_i` is `(D_i - E_i + B - C)/sqrt(A + B - 2C)` for `i in I^+` and is `(E_i - D_i + A - C)/sqrt(A + B - 2C)` for `i in I^-`. If `sqrt(A + B - 2C) - m_t < epsilon`, stop and define our output function as `f` with the current settings for `A`, `B`, and the `alpha_i`'s.
3. Adaptation:
   1. If `t in I^+'`, then set `alpha_i := (1-q)alpha_i + q delta_{i,t}` for `i in I^+`, where `q = min(1, (A - D_t + E_t - C)/(A + K(vec{x}'_t, vec{x}'_t) - 2(D_t - E_t)))`.
      Set `A := A (1-q)^2 + 2(1 - q)q D_t + q^2K(vec{x}'_t, vec{x}'_t)`, `C := (1 - q) C + q E_t`, and for `i in I` set `D_i = (1-q)D_i + q K(vec{x}'_i, vec{x}'_t)`.
   2. If `t in I^-'`, then set `alpha_i := (1-q)alpha_i + q delta_{i,t}` for `i in I^-`, where `q = min(1, (B - E_t + D_t - C)/(B + K(vec{x}'_t, vec{x}'_t) - 2(E_t - D_t)))`.
      Set `B := B (1-q)^2 + 2(1 - q)q E_t + q^2K(vec{x}'_t, vec{x}'_t)`, `C := (1 - q) C + q D_t`, and for `i in I` set `E_i = (1-q)E_i + q K(vec{x}'_i, vec{x}'_t)`.

Quiz

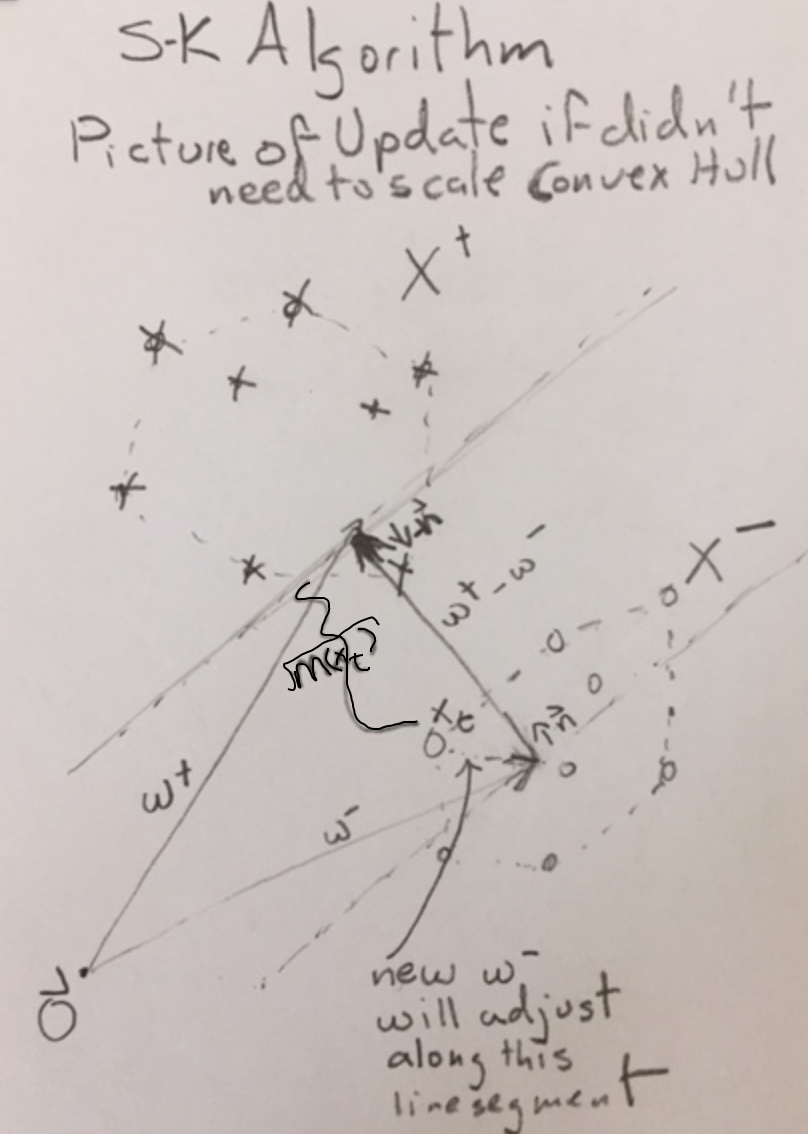
Which of the following is true?

1. We showed `MAJ_n` cannot be computed by a two layer perceptron network.
2. Our result about three layer threshold circuits being able to compute arbitrary boolean functions relied on padding some gates with 0 and 1 as inputs.
3. The shape of a `mu`-reduced convex hull of a set of points is always geometrically similar (formal def) to that of the convex hull of those points.

Numpy

• For HW2, I'd like you to use Numpy as you code your implementation of the S-K algorithm.
• Numpy is a library of functions initially proposed by Travis Oliphant in 2005 based on earlier work of Jim Hugunin useful for manipulating arrays in Python in a convenient way.
• It is implemented in a way so that it is faster than doing the same kind of thing with lists.

Importing and using Numpy

• To import numpy, you simply add to your code:

  import numpy
  

  or

  import numpy as np
  

• The basic building block in numpy is the array.
• To declare an array, we can do things like:

  a = np.array([2, -1, 4, -8], float)
  
  type(a) #outputs <type 'numpy.ndarray'>
  

• Notice we specify the type of the components.

Array Creation and Assignment

• Most reasonable "array-like" things such as tuples, etc can be used to create an array:

  a = np.array((1,2,3), float)
  a = np.array(range(1,5), float) # array([ 1.,  2.,  3.,  4.])
  a = np.arange(1,5, dtype=float) # this used a numpy method 
         #but also gives array([ 1.,  2.,  3.,  4.])
  a = np.arange(1,5,2, dtype=float) # array([ 1.,  3.]) (used a stride of 2)
  

• Numpy supports several ways of creating new arrays of a particular kind:

  np.zeros(5, dtype=float) # array([ 0.,  0.,  0.,  0.,  0.])
  np.ones((3,2), dtype=int) # array([[1, 1], [1, 1], [1, 1]]) # can give a shape
  np.identity(3, dtype=float) # 3x3 identity matrix
  np.random.rand(5) # an array of size 5 with random values between 0 and 1
  np.random.rand(3, 4) # 3 x 4 array of random values between 0 and 1
  

• Once we have an array we can assign or copy it:

  b = a #copy by reference
  b[1] = 4
  a # array([1, 4, 3])
  c = a.copy() # a new array with the same entries as a
  c[1] = 5
  a # array([1, 4, 3])
  

Shape and Content of Numpy Arrays

• Arrays can be multi-dimensional:

  a = np.array([[1, 2, 3], [4, 5, 6]], float) # a 2D array
  b = np.array([[[1,2], [2, 3]], [[4, 5], [6,7]]], float) # a 3d array
  

• We can find and manipulate the shape of a numpy array:

  len(a) # 2 (the length of the first axis)
  a.shape # (2,3)
  a.reshape(6, 1) # array([[ 1.], [ 2.], [ 3.], [ 4.], [ 5.], [ 6.]]) 
  c = b.flatten() # array([ 1.,  2.,  2.,  3.,  4.,  5.,  6.,  7.])
  

• We can also manipulate the content of arrays:

  b = np.array([ 3.,  4., 1., 5.,  6., 2., 7.]) #notice type inference
  b.sort(); # now b is array([ 1.,  2.,  2.,  3.,  4.,  5.,  6.,  7.])
  b.fill(4) # now b will contain array([ 4.,  4.,  4.,  4.,  4.,  4.,  4.,  4.])
  

Element Access

• Accessing array elements is done in the natural way:

  a[1][2] # outputs 6.0 on array a above
  b = np.array([2, -1, 4, -8], float)
  b[1] #outputs -1.0
  b[2:] #outputs [4, -8.0]
  

• We can use in to determine if an element is in an array and we can use it to cycle over arrays:

  b = np.array([2, -1, 4, -8], float)
  -8 in b #True
  for elt in b:
     print(elt)
  

Operations on Arrays

• Arrays support a variety of slicing operations:

  a = np.array([[1, 2, 3], [4, 5, 6]], float)
  b = a[1,:] #now b is array([ 4., 5., 6.])
  c = a[:,2] # now c is array([ 3., 6.])
  

• numpy has methods for common aggregation functions:

  a = np.array([1, 2, 3, 5], int)
  a.sum() # 11
  a.prod() #30
  a.mean() # 2.75
  np.median(a) # 2.5
  a.var() # 2.1875
  a.min() # 1
  a.max() # 5
  a.argmin() # 0
  a.argmax() # 3
  

• We can add and multiply two arrays like vectors or matrices of the same shape, this is always done in a point-wise fashion:

  a = np.array([1, 2, 3], int)
  b = np.array([4, 5, 6], int)
  a + b # array([5, 7, 9])
  a * b # array([ 4, 10, 18]) # notice point-wise multiplication (Hadamard product)
  b / a # array([4, 2, 2])
  b % a # array([0, 1, 0])
  b ** a # array([  4,  25, 216])
  
  a = np.array([[1, 2], [4, 5]], int)
  b = np.array([[5, 4], [1, 2]], int)
  a + b # array([[6, 6], [5, 7]])
  a * b # array([[ 5,  8], [ 4, 10]]) # notice Hadamard product
  

• Many functions can also be applied in a point-wise fashion to each element of an array, such as abs, ceil, floor, rint, exp, log, log10, sqrt, sin, cos, tan, arcsin, etc.:

  a = np.array([1, 2, 3], float)
  np.exp(a) # array([  2.71828183,   7.3890561 ,  20.08553692])
  

• Boolean Operations like <, ==, etc can also be applied point-wise

  a = np.array([1, 2, 3], int)
  b = np.array([4, 5, 3], int)
  z = a == b # array([False, False, True], dtype=bool)
  np.logical_not(z) # array([ True,  True, False], dtype=bool)
    #numpy also support logical_and(z, w)  and logical_or(z, w)
  

Linear Algebra and Polynomials

• It is easy to take the transpose of an array:

  a.transpose()
  

• Given two vectors we can take their dot product, cross product, inner, or outer product:

  a = np.array([1, -1, 1], float)
  b = np.array([3, -2, 4], float)
  np.dot(a, b) # 9.0
  np.cross(a,b) # array([-2., -1.,  1.])
  

• On 2d-arrays dot performs a matrix multiply:

  a =  np.array([[2,3],[4,5]], int)
  b = np.array([[0,3],[0,5]], int)
  np.dot(a,b) # array([[ 0, 21], [ 0, 37]])
  

• Determinants, Matrix Inverses, Eigenvalues and Eigenvectors, SVD, etc can be computed using the linalg sub-module:

  a =  np.array([[2,3],[4,5]], int)
  np.linalg.det(a)  # -2.0
  np.linalg.inv(a) #array([[-2.5,  1.5], [ 2. , -1. ]])
  eivals, eivecs = np.linalg.eig(a)
  eivals # array([-0.27491722,  7.27491722])
  eivecs # array([[-0.79681209, -0.49436913], [ 0.60422718, -0.86925207]])
  

• Numpy can also add (polyadd), subtract (polysub), divide, (polydiv) multiply (polyadd), find roots (root), integrate (polyint), take derivatives (polyder), least squares fit (polyfit), etc polynomials:

  np.roots([1,2,-3]) # array([-3.,  1.]) 
      #roots of polynomial x^2 + 2x - 3
  np.poly([1,2,3,4]) # array([  1, -10,  35, -50,  24]) 
      #coeff's of poly with roots 1,2,3,4