Outline

• SVM Training Algorithm
• In-Class Exercise

Introduction

• On Monday, we began talking about SVMs (Support Vector Machines) (Cortes Vapnik 1995).
• These are different than perceptrons in three main ways:
  1. An SVM is computed by taking the inputs, applying a vector-valued function `vec{f}:RR^n -> RR^m` and then sending the result to a perceptron gate. The hope is that `vec{f}` maps the underlying classification problem into a space where it is separable. (We showed if you allowed `m` to be big enough this is always possible.)
  2. The computation of the weights for the perceptron portion of the SVM is done by computing a maximal margin separator of the classes being separated. Doing this will likely mean the model will generalize to new data better than if the weights were determined by the perceptron or Winnow rules. This is because in the latter cases, the separating hyperplane might be closer to one of the two classes than the other.
  3. SVM training often makes use of soft margin techniques (haven't talked about yet) to handle the case where the data received by the perceptron is not separable.
• We said that the usual way to find the separator for an SVM is by solving a quadratic program (a system of quadratic inequalities).
• The SVM one gets is a threshold of terms like `vec{f}(vec{x}) cdot f(vec{x_j})`. The kernel trick involves avoiding the computation of `vec{f}` by directly computing a simpler function `k(vec{x}, vec{x_j})` for some kernel function `k`. Here `k` usually involves computing a dot-product `vec{x} cdot vec{x_j}` in the original space followed by a simple function of the reals.
• We gave three example kernels: polynomial, RBF, and two layered perceptron.
• Today, we start by talking about a way to compute close to maximal separators efficiently while avoiding directly solving any quadratic programs.
• This approach will also work in the soft margin setting.

Iterative Algorithms for Maximal Separators

• B. N. Kozinec (1973) developed an update rule for separators that was used by Schlesinger, Kalmykov, Suchorukov (1981) as the basis for an algorithm to find an `epsilon`-approximation of the maximal separator. Both of these papers were in Russian and relatively unknown in the West.
• Franc and Hlavac (2003) called Schlesinger et al's algorithm, the S-K algorithm, and showed how to extend it to work well with kernels.
• Mavroforakis, Sdralis, Theodoridis (2006) showed how to get the S-K kernel algorithm to work with respect to finding separators for reduced convex hulls (an idea from Crisp and Burges 1999), allowing one to compute reasonable separators even in the case where the data was not completely separable.
• Liu, Liu, Pan, Wang (2009) looked at scaled convex hulls, rather than reduced convex hulls, and showed how to modify the S-K algorithm to that situation. The separators on scaled convex hulls were shown to converge to the soft max margins that would be computed by quadratic programming as per the original Cortes Vapnik paper.
• In Liu et al's experiments, their version of the S-K algorithm computed a separator that achieved about the same success rate as the traditional quadratic programming approach but using about 1/3 the number of kernel evaluations and running between 2-3 times faster on large data sets.
• Today, we will look at this Liu et al's algorithm...

Convex Hulls and Their Variants

• A set `C subset RR^n` is convex if for any `vec{x}, vec{y} in C` the line segment between them, `{vec{z} | vec{z} = u vec{x} + (1 -u)vec{y} mbox( where ) u in [0,1] }`, is also in `C`.
• Given a set of points `X subseteq RR^n`, the convex hull of `X`, `conv(X)`, is the smallest convex set which contains `X`. Since `RR^n` is convex and contains `X`, and since the convex sets containing `X` can be partially ordered by inclusion, we know `conv(X)` exists.
• When `X` is finite, say because it comes from either the positive or negative examples of training task, then `conv(X)` will be:
  `{w | w = sum_{i=1}^k a_i vec{x}_i, 0 le a_i, sum_{i=1}^k a_i = 1, mbox( where each ) vec{x}_i in X}.`
• In the finite case, usually only some of the points in `X` will be on the boundary of convex hull and the rest will be interior to it. The points in `X` on the boundary of `conv(X)` in 2D form a polygon. When we give an algorithm for convex hulls we are usually asking to find the points in `X` on the boundary of the hull, as these suffice to determine the set of interior points.
• For a finite set of points `X subset RR^n` and `mu < 1`, we define the `mu`-reduced convex hull of X, `R(X, mu)`, to be:
  `{\vec{w} | \vec{w} = sum_{i=1}^k a_i vec{x}_i, 0 le a_i le mu, sum_{i=1}^k a_i = 1, mbox( where each ) \vec{x}_i in X}.`
• For a set of `k` points `X ={vec{x}_1, ..., vec{x}_k} subset RR^n`, let `vec{m}=1/k sum_{i=1}^k vec{x}_i` be its centroid and let `lambda le 1`. We define the `lambda-`scaled convex hull of X, `S(X, lambda)`, to be:
  `{\vec{w} | \vec{w} = \lambda sum_{i=1}^k a_i \vec{x}_i + (1 - lambda)m, 0 le a_i le 1, sum_{i=1}^k a_i = 1, mbox( where each ) \vec{x}_i in X}.`
• From the image above we can get some intuition as to why when separating training data, the support vectors will be on the convex hull.

Remarks on Convex Hulls and Their Variants

• Convex hulls have many applications in computer graphics and video game design. For example, it is often easier to determine if the convex hulls of two objects are intersecting than directly determining if the objects themselves are intersecting.
• There are divide-and-conquer algorithms for computing convex hulls of a finite set of points in 2 and 3-dimensions which run in `O(n log n)` (See O'Rourke 1998): Roughly, sort the points by their `x` coordinate. Put first half of the points in one set, the rest in the other. Compute convex hulls of the two sub-problems and merge results).
• Given this, one strategy to find the maximal separator one might take is:
  1. Compute the convex hull of the the positive training examples, `conv (X^+)`.
  2. Compute the convex hull of the the negative training examples, `conv (X^-)`.
  3. Find the nearest points on the two hulls and consider the line segment/plane between them.
  4. Return the perpendicular bisector as the maximal margin separator.
• In 2 or 3 dimension the run time of the above can be shown to be `O(n log n)`. To handle non-separable training data one could then use either the reduced or scaled convex hulls.
• The above figure shows an examples of an original hull and interior to it on the left a `mu={1/2}`-reduced convex hull and on the right a `lambda={1/2}`-scaled convex hull. As we can see the scaled hull better retains the shape of the original figure and this gives some of the reason why it might be preferable.
• In higher dimensions, the typically greater than three inputs to an SVM situation, just writing out convex hulls can be time prohibitive (facets on `d`-dimensional hulls will typically involve `d` many points chosen as a subset of all the points in `X`). A lower bound of time `n^{lfloor d/2 rfloor}` is known (Klee 1980), with the best algorithms running in time `O(n log n+ n^{lfloor d/2 rfloor})`.

In-Class Exercise

• Consider the points: `(0,0), (1, 1/2), (1, -1/2), (2, 5), (2, -5), (3, 0)`.
• Try to apply the sketch of a convex hull algorithm I gave to these points.
• Fill in the details of the algorithm by saying:
  1. What you did in the base case.
  2. How you handled merging.
• Post your solutions to the Sep 27 In-Class Exercise thread.

Some Facts About the Scaled-Convex Hull

• When `lambda = 1`, the scaled convex hull is the usual convex hull.
• The centroid of the scaled convex hull is the same as the original convex hull.
• Given a set `X = {vec(x)_1, ..., vec(x)_k}`, we denote by `X'` the set of points in `S(X,lambda)`, `{vec(x)_i' = lambda vec(x)_i + (1 - lambda) vec{m} | i=1, ..., k}`.
• Let `X^+` and `X^-` be two sets with different centroids, `vec{m}^+ ne vec{m}^-`. Then we can choose `lambda` small enough such that `S(X^+, \lambda)` and `S(X^-, \lambda)` can be separated.
• In particular, in the above, one can show that if `r = || vec{m}^+ - vec{m}^-||`, if `r^+ = max_{vec{x}_i in X^+} ||vec{x}_i - vec{m}^+||`, and if `r^(-) = max_{vec{x}_i in X^-} ||vec{x}_i - vec{m}^-||`, then we can take any value of `lambda` such that `lambda le r/(r^+ + r^-)`.
• Since `r`, `r^+`, and `r^-` are easy to compute, if we are in a situation where the data might not be separable, we can calculate `lambda`, then run our separator algorithm on the points `X^+'` and `X^(-)'`.

S-K Algorithm - Non-Kernel Version

Suppose our training data is `X = {vec{x}_1, ..., vec{x}_k}`. Let `I = {1, ..., k}`. Let `X^+` be the positive examples, and `I^+` be the indices of the positive examples. Let `X^-` be the negative examples, and `I^-` be the indices of the negative examples. Define `X'`, `X^(+)'`, and `X^(-)'` as per the last slide.

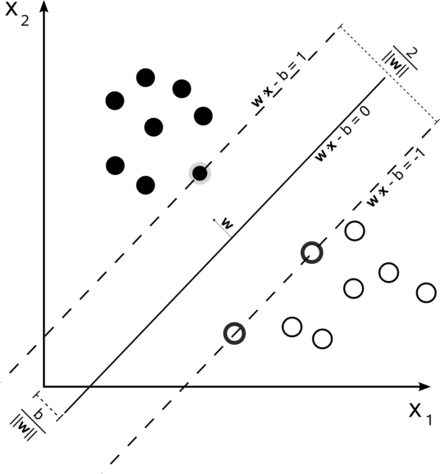
1. Initialization: Set the vector `vec{w}^{+}` to any point `x in X^(+)'` and `vec{w}^{-}` to any point `vec{x} in X^(-)'`. At each step of our algorithm our separator will be given by `vec{w} = vec{w}^{+} - vec{w}^{-}` and `theta = (||vec{w}^{+}||^2 - ||vec{w}^{-}||^2)/2`. To understand what these weights mean consider the two parallel hyperplanes, given by `vec{n}\cdot (vec{x} - vec{w}^{-}) = 0` and `-vec{n}\cdot (vec{x} - vec{w}^{+}) = 0` where `vec{n} = (vec{w}^{+} - vec{w}^{-})/(||vec{w}^{+} - vec{w}^{-}||`. These two hyperplanes are `||vec{w}|| = ||vec{w}^{+} - vec{w}^{-}||` apart. A point half-way between these hyperplanes is given by `(vec{w}^{+} + vec{w}^{-})/2`. Projecting this along the vector `vec{w} = vec{w}^{+} - vec{w}^{-}` which points between the hyperplanes, gives us `((vec{w}^{+} - vec{w}^{-}) \cdot (vec{w}^{+} + vec{w}^{-}))/2 = (||vec{w}^{+}||^2 - ||vec{w}^{-}||^2)/2 = theta`.
2. Stop Condition: Find the vector `vec{x}'_t in X'` closest to either of our current hyperplanes. To do this we choose `t = mbox(argmin)_{i in I} m(vec{x}'_i)` where `m(vec{x}'_i)` is `vec{n}\cdot(vec{x}'_i -vec{w}^{-})` for `i in I^+` and is `-vec{n}\cdot (vec{x}'_i -vec{w}^{+})` for `i in I^-`. The sign of `m(vec{x}'_t)` indicates which side of hyperplane on. For the hyperplane to classify the corresponding data correctly, we want the sign to be positive, however, we'll be satisified if the sign is only slightly negative. More precisely, if `||vec{w}^{+} - vec{w}^{-}|| - m(vec{x}'_t) < epsilon`, stop output `vec{w}` and `theta` given by the formulas above.
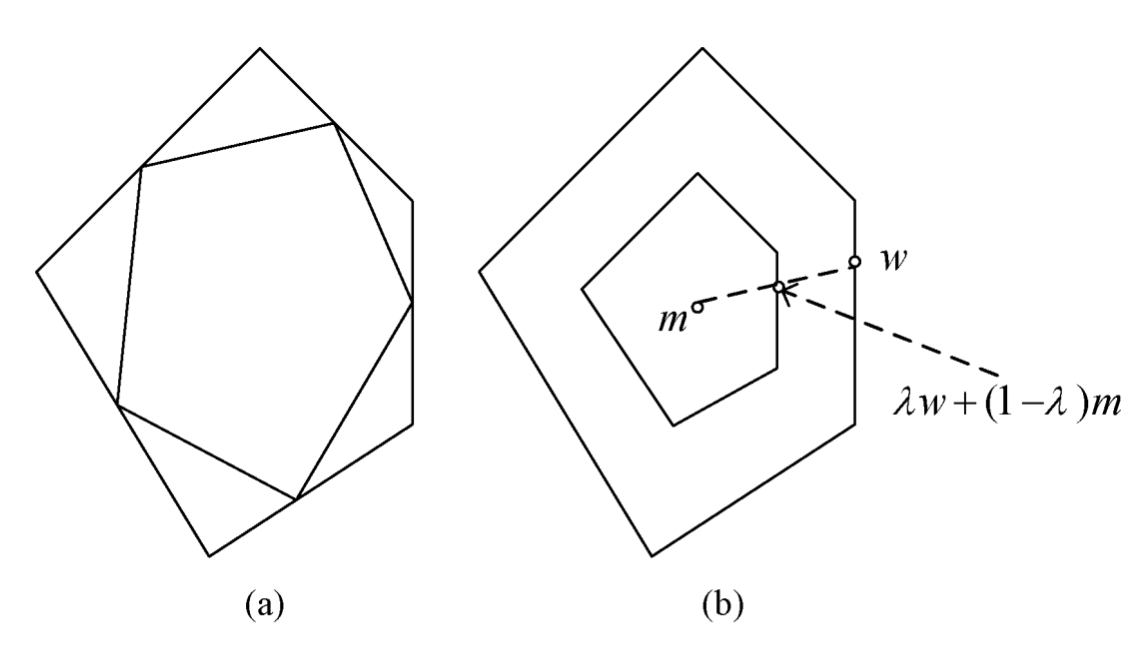
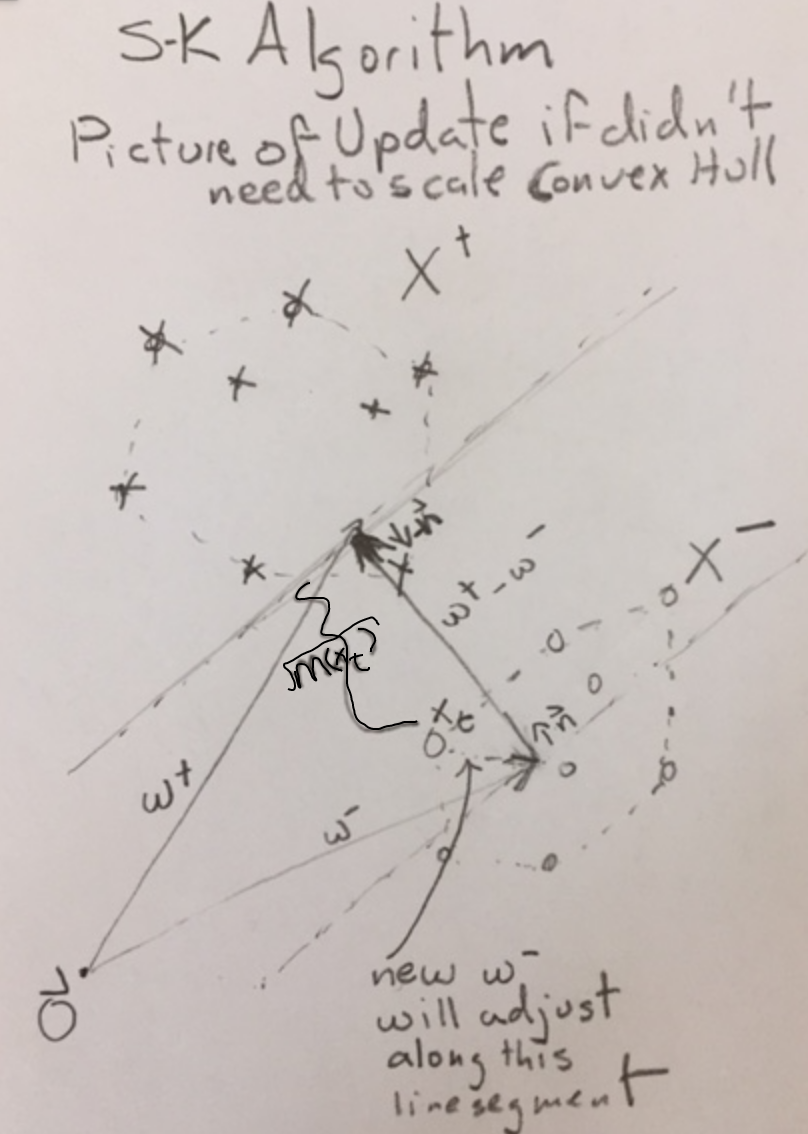
3. Adaptation: If `vec{x}'_t in X^+'`, set `vec{w}^{-} := vec{w}^{-}` and set `vec{w}^{+} := (1-q) vec{w}^{+} + q vec{x}'_t` where `q = min(1, ((vec{x}'_t -vec{w}^{-})\cdot(vec{w}^{+} - vec{w}^{-}))/(||vec{w}^{+} - vec{w}^{-}||^2))`; otherwise, set `vec{w}^{+} := vec{w}^{+}` and set `vec{w}^{-} := (1-q) vec{w}^{-} + q vec{x}'_t` where `q = min(1, ((vec{x}'_t -vec{w}^{+})\cdot(vec{w}^{-} - vec{w}^{+}))/(||vec{w}^{+} - vec{w}^{-}||^2))`.

S-K Algorithm - Intuitions

• At any step in the algorithm `vec{w}^{+}` is a linear combination of elements in `X^+'` and `vec{w}^{-}` is a linear combination of elements in `X^(-)'`.
• So as `X^+'` and `X^-'` are separable `||vec{w}^{+} - vec{w}^{-}||` is always greater than or equal to some minimal distance between these sets.
• So if `m` is within distance `epsilon` of being on the correct side of its hyperplane and at the minimal needed distance, we stop.
• Otherwise, we adjust `vec{w}^{\pm}`'s so as to make `vec{x}'_t` more close to being on the correct side of its hyperplane, by making `vec{x}'_t` a support vector and `vec{w}^{\pm}` a linear combination of `vec{x}'_t` and the existing vectors. Notice if we are way off, we'll get `q=1` and we set `vec{w}^{\pm} = vec{x}'_t` to do this.
• The proof of correctness of this step is given in Franc and Hlavac and is similar to the proof of perceptron convergence, we have a potential function (the current `||vec{w}^{+} - vec{w}^{-}||`) which is always decreasing by a constant amount each iteration and which is bounded below by the minimum distance between the convex hulls `conv(X^+)` and `conv(X^-)`.

S-K Algorithm - Kernel Version - Preliminaries

• We now replace dot products in the previous algorithm with the use of kernels...
• Suppose our training data is `X = {vec{x}_1, ..., vec{x}_k}`. Let `I = {1, ..., k}`. Let `X^+` be the positive examples, and `I^+` be the indices of the positive examples. Let `X^-` be the negative examples, and `I^-` be the indices of the negative examples. Let `y_i = 1` if `x_i in X^+` and `y_i = -1` otherwise. Define `X'`, `X^(+)'`, and `X^(-)'` as per two slides ago.
• Let `delta_{i,t}` be 1 if `i = t` and 0 otherwise.
• If `K(vec{x}, vec{x}')` is the kernel function we are using, our final SVM will compute `g(vec{x}) = sign(sum_{i in I} alpha_i y_i K(vec{x}, vec{x}'_i) + (B - A)/2)`. Here `alpha_i in RR` will typically be 0 except for a small number of `i`'s, `A, B in RR` are constants we will define in a moment.
• If we imagine that, the non-linear map that the SVM is supposed to compute before apply a perceptron gate is: `vec{f}:RR^n -> RR^m`. Then the kernel `k(vec{x}, vec{z})` is supposed to replace `vec{f}(vec{x})cdot f(vec{z})`. `alpha_i`'s in `g` will be nonzero in the above only if `vec{f}(vec{x}'_i)` is a support vector.
• If in the non-kernel version of the algorithm we need to compute an expression like: `(vec{x}'_t -vec{w}^{-})\cdot(vec{w}^{+} - vec{w}^{-})` to make a kernel version we will first expand this as `vec{x}'_t\cdot vec{w}^{+} - vec{x}'_t\cdot vec{w}^{-} - vec{w}^{-}\cdot vec{w}^{+} + vec{w}^{-}\cdot vec{w}^{-}`. Roughly, the kernel can be applied to each term in the expression: `K(vec{x}'_t, vec{w}^{+}) - K(vec{x}'_t, vec{w}^{-}) - K(vec{w}^{-}, vec{w}^{+}) + K(vec{w}^{-}, vec{w}^{-})` to get the kernelized analog.

S-K Algorithm - Kernel Version

Algorithm:

1. Initialization: Set `alpha_(i_1) = 1` for `i_1 in I^+`, `alpha_(j_1) =1` for `j_1 in I^-`. Set all the remaining `alpha_i = 0`. Set `A = K(vec{x}'_{i_1}, vec{x}'_{i_1})`, `B = K(vec{x}'_{j_1}, vec{x}'_{j_1})`, `C= K(vec{x}'_{i_1}, vec{x}'_{j_1})`. For `i in I` define `D_i = K(vec{x}'_{i}, vec{x}'_{i_1})` and `E_i = K(vec{x}'_{i}, vec{x}'_{j_1})`.
2. Stop Condition: Find the vector `vec{x}'_t in X'` closest to our current separating hyper-surfaces. To do this we choose `t = mbox(argmin)_{i in I} m_i` where `m_i` is `(D_i - E_i + B - C)/sqrt(A + B - 2C)` for `i in I^+` and is `(E_i - D_i + A - C)/sqrt(A + B - 2C)` for `i in I^-`. If `sqrt(A + B - 2C) - m_t < epsilon`, stop and define our output function as `f` with the current settings for `A`, `B`, and the `alpha_i`'s.
3. Adaptation:
   1. If `t in I^+'`, then set `alpha_i := (1-q)alpha_i + q delta_{i,t}` for `i in I^+`, where `q = min(1, (A - D_t + E_t - C)/(A + K(vec{x}'_t, vec{x}'_t) - 2(D_t - E_t)))`.
      Set `A := A (1-q)^2 + 2(1 - q)q D_t + q^2K(vec{x}'_t, vec{x}'_t)`, `C := (1 - q) C + q E_t`, and for `i in I` set `D_i = (1-q)D_i + q K(vec{x}'_i, vec{x}'_t)`.
   2. If `t in I^-'`, then set `alpha_i := (1-q)alpha_i + q delta_{i,t}` for `i in I^-`, where `q = min(1, (B - E_t + D_t - C)/(B + K(vec{x}'_t, vec{x}'_t) - 2(E_t - D_t)))`.
      Set `B := B (1-q)^2 + 2(1 - q)q E_t + q^2K(vec{x}'_t, vec{x}'_t)`, `C := (1 - q) C + q D_t`, and for `i in I` set `E_i = (1-q)E_i + q K(vec{x}'_i, vec{x}'_t)`.