










Perceptron Networks and p-time algorithms, SVMs
CS256
Chris Pollett
Sep 25, 2017











CS256
Chris Pollett
Sep 25, 2017

Theorem. A `p(n)`-time algorithm for a 1-tape TM can be simulated by a `O(p(n))`-layer threshold network of size `O(p(n)^2)`. Moreover, the `O(p(n))`-layers, are built out of 1 layer which maps the input to an encoding of input, followed `p(n)`-many `O(1)`-layer networks each of which compute the same function `L`, followed by a layer which maps the encoding of the output to the final output . An `L` layer can be further split into `p(n)` many threshold networks each of size `O(1)` with `O(1)` inputs computing the same function `U` in parallel.
Remark. Imagine we were trying to learn a `p`-time algorithm. The result above says that we just need to learn the `O(1)` many weights in the repeated `U`, not polynomially many weights as you might initially guess. We can think of `U` as roughly corresponding to the neural nets finite control. The idea of using repeated sub-networks each of which use the same weights is essentially the idea behind convolutional neural layers.
Which of the following is true?
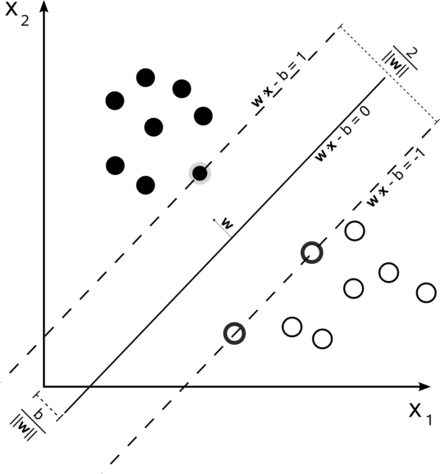
Theorem. It is always possible to map a dataset of examples `(vec{x}, y_i)` where `vec{x} in RR^n` and `y_i in {0,1}` to some higher dimensional `vec{f}(vec{x}) in RR^m` such that the negatives examples `vec{f}(vec{x_j})` can be separated from the positive examples `vec{f}(vec{x_k})` by a hyperplane in `RR^m`.
Proof. Let `f_(vec{z})(vec{x})` be the function which is `0` if `vec{x} ne vec{z}` or if `vec{z}` was not a positive training example and is `1` otherwise. Let `vec{f}` be the mapping from `RR^n -> RR^{2^n}` given by `vec{x} mapsto (f_{vec{0}}(vec{x}), ...,f_(vec{z})(vec{x}), ..., f_{vec{1}}(vec{x}))`. All of the negative examples will map to the `0` vector of length `2^n` and a positive example will map to a vector with exactly one coordinate 1. Hence, the hyperplane which cuts each axis in the target space at a `1/2` will separate the positive from the negative examples. Q.E.D.
Corollary. Any boolean function can be computed by an SVM (maybe slightly relaxing the definition of maximally separate to allow for unbounded support vectors).
Remark. The above construction gives an SVM which does not generalize very well, so it is not really a practical construction.
Remark. For SVMs, usually `y_i`'s are chosen from `{-1, 1}`, but a similar theorem to the above could still be obtained.