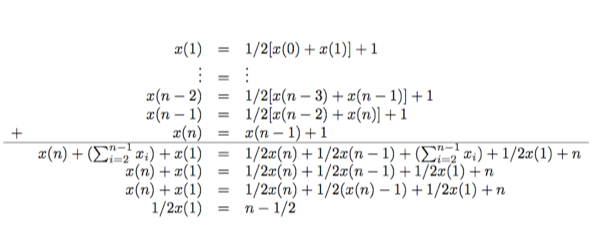Outline

• Aproximation Algorithms
• Approximation Algorithm for Vertex Cover
• Quiz
• Approximation Algorithm for TSP
• A TSP Inapproximibility Result

Approximation Algorithms, Performance Ratios

• Since it seems hard to find exact solutions to the optimization problems associated with a given `NP`-complete problem, it is natural to ask if one can get approximate solutions in polynomial time?
• We say an algorithm for a problem has an approximation ratio of `r(n)`, if for any input of size `n`, the cost `C` of the solution produced by the algorithm is within a factor of `r(n)` of the cost `C^star` of the optimal solution. That is, `max(C/C^star, C^star/C) le r(n)`.
• We call an algorithm that achieves an `r(n)`-approximation ratio an `r(n)`-approximation algorithm.
• Some `NP`-complete problems have a trade-off between the approximation ratio and the run time.
• An approximation scheme for an optimization problem is an algorithm that takes both an instance of the problem as well as a constant `epsilon` and then runs a `(1 + epsilon)`-approximation on the instance.
• If for any `epsilon`, the approximation scheme run in `p`-time, then it is called a polynomial time approximation scheme.
• We say that an approximation scheme is a fully `p`-time approximation scheme if it is an approximation scheme and its run time is `p`-time in both `1/epsilon` and the instance size `n`. For example, the scheme might have a running time of `O((1/epsilon)^2n^3)`.

The Vertex Cover Problem

• The optimization problem associated with VERTEX-COVER is to find the least vertex cover of a instance graph `G`.
• The following algorithm takes a graph `G` and outputs a vertex cover within twice the optimal.

APPROX-VERTEX-COVER(G)
1 C=∅
2 E'= E[G]
3 while E' ≠ ∅
4    let {u, v} be an arbitrary edge of E'
5    C = C ∪ {u, v}
6    Remove from E' every edge incident with either u or v
7 return C.

Analysis of APPROX-VERTEX-COVER

Theorem. APPROX-VERTEX-COVER is a p-time 2-approximation algorithm.

Proof. First, the algorithm runs in time `O(|V| +|E|)`, as we delete two vertices and at least one edge each time through the loop.

The set `C` returned by the algorithm is a vertex cover, since each edge that is removed is covered by some vertex in `C`. And the loop continues till no edges left.

To see that the cover returned is at most twice the optimal, let `A` denote the set of edges which were picked in line 4. In order to cover the edges in `A`, any vertex cover (including the optimal `C^star`) must include at least one endpoint of each edge in `A`. No two edges in `A` share an endpoint, so no two edges from `A` are covered by the same vertex from `C^star`. So `|C^star | ge |A|`. On the other hand `|C| = 2|A|`.

Quiz

Which of the following statements is true?

1. Even if `P ne NP`, whether there is a permutation of vertices of a graph `G` such that between every pair of adjacent vertices (we count the first and last vertices in permutation as adjacent) in the permutation there is an edge in `G` is NP-complete.
2. Even if `P ne NP`, whether a graph has a clique of size three is NP-complete.
3. The traveling salesman problem is in `P` if the cost between cities is always 0 or 1.

Approximating the Traveling Salesman Problem

• The optimization problem associated with TSP is to find a tour of least cost.
• Here is a 2-approximation algorithm for this problem when the triangle inequality holds on the distances between cities.

APPROX-TSP-TOUR(G, c)
1. Select a vertex r to be a root vertex
2. Compute the minimal spanning tree for G from root r using Prim's algorithm
3. Let L be the list of vertices visited in a pre-order tree walk of T
4. return the Hamiltonian cycle H that visits the vertices in order L.

Subroutines used by our algorithm

• Recall in a pre-order traversal of a graph starting from some node, we visit each child we have not yet visited, and then visit the current node.
• Recall Prims algorithm contructs a minimal spanning tree from a tree so far, denoted `A`, which at the start of the algorithm is the empty tree.
• We maintain a priority queue of all the vertices not in A.
• The priority, `v.key`, for a vertex `v` in the queue is the least weight of any edge connecting `v` with `A`. If no such edge exists than it is `infty`.
• Let `v.pi` be the parent of `v` in the tree. Rather than explicitly have an `A` we use this parent structure to get the tree when the algorithm terminates.
• Here is the pseudo-code:

  MST-PRIM(G, w, r) // r is a starting node to grow the tree from
  01 for each u in G.V
  02    u.key = infty
  03    u.pi = NIL
  04 r.key = 0
  05 r.pi = 0;
  06 Q = MAKE-QUEUE(G.V) //will have all vertices
  07 while Q != 0
  08     u = EXTRACT-MIN(Q)
  09     for each v in G.adj[u]
  10        if v in Q  and u.key + w(u, v) < v.key
  11            v.pi = u
  12            v.key = u.key + w(u,v) //call appropriate DECREASE-KEY
  

Analysis of APPROX-TSP-TOUR

Theorem. APPROX-TSP-TOUR is a p-time 2-approximation algorithm for TSP with triangle-inequality holding on the cost function.

Proof. The minimal spanning tree algorithm runs in time `O(|V|^2)`. The remaining step take at most `O(|G|)` time.

Let `H^star` denote the optimal tour of the vertices. Since we can obtain a spanning tree from any tour by deleting an edge, we have `c(T) le c(H^star)` where `T` is our minimal spanning tree. A full walk `F` of `T` lists the vertices when they are first visited and also whenever they are returned to after a visit to a subtree. So `c(F) = 2c(T) le 2c(H^star)`. A full walk is typically not a tour since it lists some vertices twice.

On the other, the `H` returned by the algorithm is a tour and satisfies `c(H) le c(F)`, since it is obtained by deleting vertices from the full walk and since the triangle inequality holds. We are using the triangle inequality as if we have a sequence `a b c` in the full walk and delete `b`, in our tour we want that the cost does not rise.

General TSP

Theorem. If `P ne NP`, then for any constant `d ge 1`, there is no `p`-time approximation algorithm with approximation ratio `d` for general TSP.

Proof. Suppose that for some number `d ge 1`, there was an approximation algorithm `A` for general TSP with the given approximation ratio. Without loss of generality, we can assume `d` is an integer. We will then show how to use `A` to solve instances of HAM-CYCLE. Since HAM-CYCLE is NP- complete, this will imply the result...

Proof of Inapproximability of General TSP cont'd

Let `G = (V, E)` be an instance of the HAM-CYCLE problem. Let `G'= (V, E')` be the complete graph on `V`. Assign a cost to each edge in `E'` as follows:
`c(u,v) = {(1,mbox(if ){u,v} in E),(d cdot |V| + 1,mbox(otherwise.)):}`

This instance `(G', c)` of the TSP optimization problem can be created in p-time in the HAM-CYCLE instance length. If the original graph has a Hamiltonian cycle, then there is a tour following its edges of cost `|V|`. On the other hand, if no such tour exists, then a tour uses at least one edge not in `E`, so has cost `(d cdot |V| +1) + (|V| - 1) > d cdot |V|`. Since our approximation algorithm needs to find a tour within a factor of `d` of the smallest one, if there is a Hamiltonian cycle in `G` when we run `A` the tour output will have cost `le d cdot|V|`. On the other hand, if the graph G does not have a hamiltonian cycle our algorithm on this instance will return a value `> d cdot|V|`.

The Set Covering Problem

• Set covering was one of the 21 `NP`-complete problems given by Karp in 1972.
• It models a variety of resource selections problems.
• An instance `(X, F)` of the set covering problem consists of a finite set `X` and a family of subsets of `X`, `F`, such that every element of `X` belongs to at least one subset of `F`. I.e., `X = cup_(S in F) S`.
• We say that a subset of `S in F` covers its elements.
• The set cover optimization problem is to find a minimum-sized subset `C subseteq F` whose members cover all of `X`. I.e., `X = cup_(S in C) S`.
• In the above picture, we have a set `X` of 12 elements, and we have a set `F = {S_1, ..., S_6}` of subsets of `X`. The set `C={S_3, S_4, S_5}` is a minimal cover.
• The NP-complete decision problem is to determine if `(X, F)` has a set cover of size `k`.

Example Use of Set Cover

• Suppose `X` represents a set of skills that are needed to solve a problem.
• `F` might be a set of people each of which have some of these skills.
• We might want to find a team `C` of as few people as possible that together have all the skills needed to solve the problem.

Greedy Algorithm For Set Covering

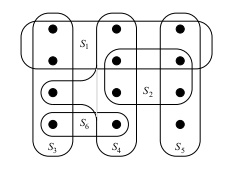
One can give a greedy algorithm for finding a cover by picking the set `S` at each stage that covers the greatest number of remaining elements that are uncovered.

GREEDY-SET-COVER(X, F)
1 U := X
2 C := ∅
3 while U ≠ 0
4     select an S ∈ F that maximizes {S ∩ U}
5     U := U - S
6     C := C ∪ {S}
7 return C

Approximation Result for Set Cover

Let `H(d) = sum_(i=1)^d 1/i` denote the `d`th harmonic number, defining `H(0) = 0`.

Theorem. GREEDY-SET-COVER is a polynomial-time `r(n)`-approximation algorithm, where
`r(n) = H(max{|S| : S in F})` on instances `(X,F)` or size `n`.

Proof. GREEDY-SET-COVER deletes at least one `S` from `F` in each iteration and the select step is at most quadratic time, so the algorithm will be polynomial time in the instance size.

To see that GREEDY-SET-COVER is an `r(n)`-approximation algorithm, we assign a cost of `1` to each set selected by the algorithm, distribute this cost over the elements covered for the first time, and then use these costs to derive the desired relationship between the size of an optimal set cover `C^star` and the size the cover `C` returned by the algorithm...

Proof of Approximation Result for Set Cover cont'd

Let `S_i` denote the `i` set selected by GREEDY-SET-COVER. We spread the cost of selecting `S_i`, 1, evenly among the elements covered for the first time by `S_i`. Let `c_x` denote the cost allocated to element `x in X`. If `x` is covered by `S_i`, then
`c_x = 1/(|S_i - (S_1 cup S_2 cup ... cup S_(i-1))|)`.
At each step of the algorithm, 1 unit of cost is assigned, and so
`|C| = sum_(x in X)c_x`.
The cost of the optimal cover is `sum_(S in C^star)sum_(x in S)c_x`,
and as each `x in X` is in at least one `S in C^star`, we have
`sum_(S in C^star)sum_(x in S)c_x ge sum_(x in X)c_x = |C|` (**).

We will show the theorem follows from the following claim:

Claim.`sum_(x in X)c_x le H(|S|)` for all `S in F`.

(Proof of Theorem from Claim). From (**) and the claim, we have
`|C| le sum_(S in C^star) H(|S|)`
`le |C^star| cdot H(max{|S| : S in F})`

Proof of Element Cover Cost Claim

Consider any `S in F` and `i = 1, ..., |C|`. Let
`u_i = |S - (S_1 cup S_2 cup ... cup S_(i))|`.
We define `u_0 = |S|`. Let `k` be the least index such that `u_k = 0`. At `k`, each element in S will be covered by at least one of `S_1, ... S_k`. We have `u_(i-1) ge u_i`, and that `u_(i-1) - u_i` elements of `S` are covered for the first time by `S_i`. Thus,
`sum_(x in S)c_x = sum_(i = 1)^k(u_(i-1) - u_i) cdot 1/(|S - (S_1 cup S_2 cup ... cup S_(i -1))|)`
Observe that
`|S_i - (S_1 cup S_2 cup ... cup S_(i - 1))| ge |S - (S_1 cup S_2 cup ... cup S_(i - 1))| = u_(i - 1)`
because we chose `S_i` greedily. This gives
`sum_(x in S)c_x le sum_(i = 1)^k(u_(i-1) - u_i) cdot 1/(u_(i-1))`
`= sum_(i=1)^k sum_(j = u_i + 1)^(u_(i-1))1/(u_(i-1))`
`le sum_(i=1)^k sum_(j = u_i + 1)^(u_(i-1)) 1/j` (because of the start condition of sum, `j le u_(i-1)`)
`= sum_(i=1)^k ( sum_(j = 1)^(u_(i-1)) 1/j - sum_(j = 1)^(u_(i)) 1/j)`
`= sum_(i=1)^k (H(u_(i-1)) - H(u_i))`
`= H(u_0) - H(u_k)` (telescoping series)
`= H(u_0) - H(0)`
`= H(u_0)`
`=H(|S|)`, proving the claim.

Randomized Algorithm for 2-SAT

• In a moment we will look at randomized approximation algorithms, starting with one for SAT
• Before we do, I thought I'd present a cool related algorithms for 2-SAT that uses random walks to find a satisfying assignment with high probability for instances of SAT where each clause has two literals...

Random Walks for SAT

• Consider the following algorithm for satisfiability:
  1. Start with any truth assignment `T`, and repeat the following `r` times:
     1. If there is no unsatisfied clause output "Satisfiable", halt.
     2. Otherwise, take any unsatisfied clause; pick any of its literals at random and flip its value
  2. After `r` repetitions reply "the formula is probably unsatisfiable"
• Is there a good value of `r` to choose so that this algorithm works?

Random Walks for 2SAT

Theorem. Suppose that the random walk algorithm with `r=2n^2` is applied to any satisfiable instance of 2SAT with `n` variables. Then the probability that a satisfying truth assignment will be discovered is at least `1/2`.

Proof. Let `T` be a truth assignment which satisfies the given 2SAT instance `I`. Let `t(i)` denote the number of expected repetitions of the flip step until a satisfying assignment is found starting from an assignment `T'` which differs in at most `i` positions from `T`. Notice:

1. `t(0) = 0`
2. If we find some other satisfying assignment, we do not need to continue.
3. Otherwise, we flip at least once, and we have a 50% chance of moving closer to the solution; 50% farther. So `t(i) le 1/2(t(i-1) + t(i+1)) + 1`
4. We also have `t(n) le t(n-1) + 1` (If every literal is wrong, we can only move closer).

The worst case is the when relation `t` of (3) holds as an equation. `x(0)=0`; `x(n)=x(n-1)+1`; `x(i) = 1/2(x(i-1)+x(i+1))+1`

Proof Cont'd

• As you can see above, adding all the `x(i)`'s together gives: `x(1) = 2n-1`.
• Then solving the `x(1)` equation for `x(2)` gives `4n-4`, and in general, `x(i) =2 i n-i^2`.
• Thus we have shown `t(i) le x(i) le x(n)=n^2`. Now consider the following lemma:
  Lemma (Markov Inequality). If `x` is a random variable taking nonnegative integer values, then for any `k > 0`, `Pr[x ge k cdot E(x)] le 1/k`.
  Proof. Let `p_i` be the probability that `x=i`.
  `E(x) = sum_i i cdot p_i = sum_(i le k cdot E(x)) i cdot p_i + sum_(i > k cdot E(x)) i cdot p_i > k cdot E(x) cdot Pr[x>k cdot E(x)]` Q.E.D.
• The theorem then follows taking `k=2`.