










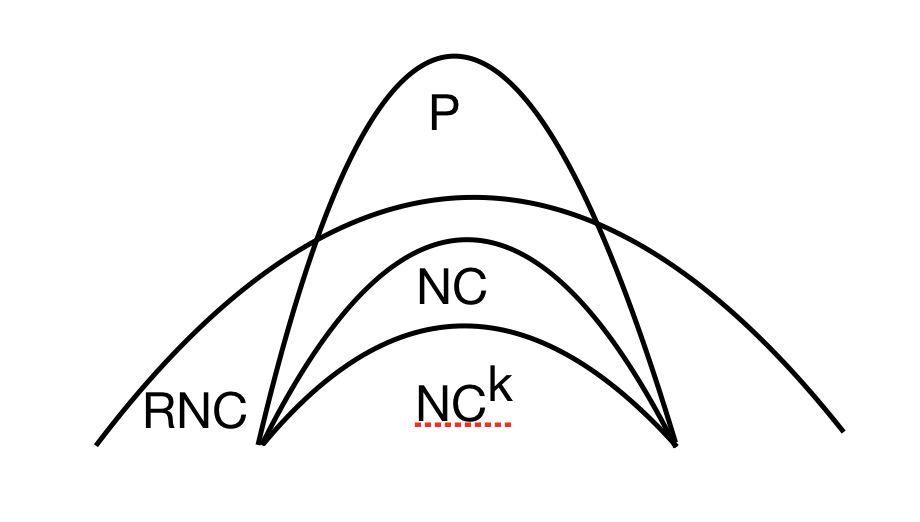
PRAMs and Maximal Independent Set
CS255
Chris Pollett
Feb 26, 2015











CS255
Chris Pollett
Feb 26, 2015
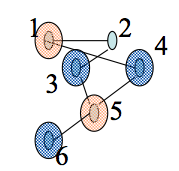
Greedy MIS:
Input: Graph G(V,E) with V = {1,..,n}
Output A maximal I contained in V.
1. I := emptyset
2. For v=1 to n do
3. If Gamma(v) intersect I = emptyset then I := I union {v}.
Which of the following statements is true?
1. Pick any vertex v 2. Add v to I 3. Delete v and Gamma(v) from the graph.
Input: G=(V,E)
Output: A maximal independent set I contained in V
1. I := emptyset
2. Repeat {
a) For all v in V do in parallel
If d(v) = 0 then add v to I and delete v from V.
else mark v with probability 1/(2d(v)).
b) For all (u,v) in E do in parallel
if both u and v are marked
then unmark the lower degree vertex.
c) For all v in V do in parallel
if v is marked then add v to S
d) I := I union S
e) Delete S union Gamma(S) from V and all incident edges from E
} Until V is empty.
Lemma*. Let `v` in `V` be a good vertex with degree `d(v) > 0`. Then, the probability that some vertex `w in Gamma(v)` gets marks is at least `1- exp(-1/6)`.
Proof. Each vertex `w in Gamma(v)` is marked independently with probability `1/(2d(w))`. Since `v` is good, there exist `(d(v))/3` vertices in `Gamma(v)` with degree at most `d(v)`. Each of these is marked with probability at least `1/(2d(v))`. Thus, the probability none of these neighbors is marked is at most: `(1 - 1/(2d(v)))^((d(v))/3) le e^((-1)/6)`.
Here we are using that `(1 + a/n)^n <= e^(a)` and that the remaining neighbors of `v` can only help increase the probability under consideration.
Lemma**. During any iteration, if a vertex `w` is marked then it is selected to be in `S` with probability at least `1/2`.
Proof. The only reason a marked vertex `w` becomes unmarked and hence not selected for `S` is if one of its
neighbors of degree at least `d(w)` is also marked. Each such neighbor is marked with probability at most
`1/(2d(w))`, and the number of such neighbors is at most `d(w)`. Hence, we get the probability that a marked vertex is
selected to be in `S` is at least:
`1 - Pr{exists x in Gamma(w) mbox( such that ) d(x) ge d(w) mbox( and x is marked )}`
`ge 1 - |{x in Gamma(w)| d(x) ge d(w)}| times 1/(2d(w))`
`ge 1 - sum_(x in Gamma(w))1/(2(d(w))`
`= 1 - d(w) times 1/(2(d(w))`
`= 1/2`
Lemma#. The probability that a good vertex belongs to `S cup Gamma(S)` is at least `(1- exp(-1/6))/2`.
Proof. Let `v` be a good vertex with `d(v) > 0`, and consider the event `E` that some vertex in `Gamma(v)` does get marked. Let `w` be the lowest numbered marked vertex in `Gamma(v)`. By Lemma **, `w` is in `S` with probability at least `1/2`. But if `w` is in `S`, then `v` belongs `S cup Gamma(S)` as `v` is a neighbor of `w`. By Lemma *, the event `E` happens with probability `1- exp(-1/6)`. So the probability `v` is in `S cup Gamma(S)` is thus `(1- exp(-1/6))/2`.
Lemma## In a graph `G=(V,E)`, the number of good edges is at least `|E|/2`.
Proof. Our original graph was undirected. Direct the edges in `E` from the
lower degree-point to the higher degree endpoint, breaking ties arbitrarily. Let `d_i(v)` be the
indegree of `v` and `d_o(v)` be the out-degree. From the definition of goodness, we have for
each bad vertex:
`d_o(v) - d_i(v) ge (d(v))/3 = (d_o(v) + d_i(v) )/3`
For all `S`, `T` contained in `V`, define the subset of the edges `E(S,T)` as those edges directed from vertices
in `S` to vertices in `T`; further, let `e(S,T) = |E(S,T)|`. Let `V_G` and `V_B` be the sets of
good and bad vertices respectively. The total degree of the bad vertices is given by:
`2e(V_B, V_B) + e(V_B, V_G) + e(V_G, V_B)`
`= sum_(v in V_B) (d_o(v) + d_i(v))`
`le 3 sum_(v in V_B)(d_o(v) - d_i(v))`
`= 3 sum_(v in V_G)(d_i(v) - d_o(v))`
`= 3[(e(V_B, V_G) + e(V_G, V_G)) - (e(V_G, V_B) + e(V_G, V_G))]`
`= 3[e(V_B, V_G) - e(V_G, V_B)]`
`le 3[e(V_B, V_G) + e(V_G, V_B)]`
The first and last expressions in this sequence of inequalities imply that
`e(V_B,V_B) <= e(V_B,V_G) + e(V_G,V_B)`.
Since every bad edge contributes edge contributes to the left side, and only
good edges to the right side, the result follows.
Theorem. The Parallel MIS algorithm has an EREW PRAM implementation running in expected time `O(log^2 n)` using `O(n+m)` processors.
Proof. Notice each round is `O(log n)` time on `O(n+m)` processors. Since a constant fraction of the edges are incident on good vertices and good vertices get eliminated with a constant probability, it follows that the expected number of edges eliminated during an iteration is a constant fraction of the current set of edges. So after `O(log n)` iteration we will have gotten down to the empty set. QED
Remark. By using pairwise independence rather than full independence in the above analysis one can show only `O(log n)` random bits are needed for the algorithm. From this one can derandomize the above algorithm to get an NC algorithm.