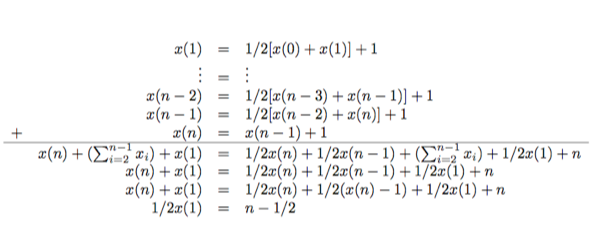Outline

• A Direct Inapproximability Result
• Set-Covering Approximation
• Approximation and SAT

Introduction

• On Monday we were talking about approximation algorithms.
• We said an algorithm for a problem has an approximation ratio of `r(n)`, if for any input of size `n`, the cost `C` of the solution produced by the algorithm is within a factor of `r(n)` of the cost `C^star` of the optimal solution. That is, `max(C/C^star, C^star/C) le r(n)`.
• We called an algorithm that achieves an `r(n)`-approximation ratio an `r(n)`-approximation algorithm.
• We gave a p-time 2-approximation algorithm for vertex cover that just repeatedly deleted edges from a graph.
• We gave p-time 2-approximation algorithm for TSP with triangle-inequality, by computing a minimal spanning tree and then traversing it in a pre-order way.
• Today, we continue with approximation algorithms and look at what happens for the general TSP case.

General TSP

Theorem. If `P ne NP`, then for any constant `d ge 1`, there is no `p`-time approximation algorithm with approximation ratio `d` for general TSP.

Proof. Suppose that for some number `d ge 1`, there was an approximation algorithm `A` for general TSP with the given approximation ratio. Without loss of generality, we can assume `d` is an integer. We will then show how to use `A` to solve instances of HAM-CYCLE. Since HAM-CYCLE is NP- complete, this will imply the result...

Proof of Inapproximability of General TSP cont'd

Let `G = (V, E)` be an instance of the HAM-CYCLE problem. Let `G'= (V, E')` be the complete graph on `V`. Assign a cost to each edge in `E'` as follows:
`c(u,v) = {(1,mbox(if ){u,v} in E),(d cdot |V| + 1,mbox(otherwise.)):}`

This instance `(G', c)` of the TSP optimization problem can be created in p-time in the HAM-CYCLE instance length. If the original graph has a Hamiltonian cycle, then there is a tour following its edges of cost `|V|`. On the other hand, if no such tour exists, then a tour uses at least one edge not in `E`, so has cost `(d cdot |V| +1) + (|V| - 1) > d cdot |V|`. Since our approximation algorithm needs to find a tour within a factor of `d` of the smallest one, if there is a Hamiltonian cycle in `G` when we run `A` the tour output will have cost `le d cdot|V|`. On the other hand, if the graph G does not have a hamiltonian cycle our algorithm on this instance will return a value `> d cdot|V|`.

The Set Covering Problem

• Set covering was one of the 21 `NP`-complete problems given by Karp in 1972.
• It models a variety of resource selections problems.
• An instance `(X, F)` of the set covering problem consists of a finite set `X` and a family of subsets of `X`, `F`, such that every element of `X` belongs to at least one subset of `F`. I.e., `X = cup_(S in F) S`.
• We say that a subset of `S in F` covers its elements.
• The set cover optimization problem is to find a minimum-sized subset `C subseteq F` whose members cover all of `X`. I.e., `X = cup_(S in C) S`.
• In the above picture, we have a set `X` of 12 elements, and we have a set `F = {S_1, ..., S_6}` of subsets of `X`. The set `C={S_3, S_4, S_5}` is a minimal cover.
• The NP-complete decision problem is to determine if `(X, F)` has a set cover of size `k`.

Example Use of Set Cover

• Suppose `X` represents a set of skills that are needed to solve a problem.
• `F` might be a set of people each of which have some of these skills.
• We might want to find a team `C` of as few people as possible that together have all the skills needed to solve the problem.

Greedy Algorithm For Set Covering

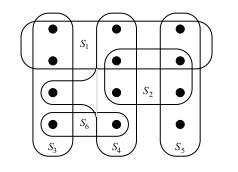
One can give a greedy algorithm for finding a cover by picking the set `S` at each stage that covers the greatest number of remaining elements that are uncovered.

GREEDY-SET-COVER(X, F)
1 U := X
2 C := ∅
3 while U ≠ 0
4     select an S ∈ F that maximizes {S ∩ U}
5     U := U - S
6     C := C ∪ {S}
7 return C

Approximation Result for Set Cover

Let `H(d) = sum_(i=1)^d 1/i` denote the `d`th harmonic number, defining `H(0) = 0`.

Theorem. GREEDY-SET-COVER is a polynomial-time `r(n)`-approximation algorithm, where
`r(n) = H(max{|S| : S in F})` on instances `(X,F)` or size `n`.

Proof. GREEDY-SET-COVER deletes at least one `S` from `F` in each iteration and the select step is at most quadratic time, so the algorithm will be polynomial time in the instance size.

To see that GREEDY-SET-COVER is an `r(n)`-approximation algorithm, we assign a cost of `1` to each set selected by the algorithm, distribute this cost over the elements covered for the first time, and then use these costs to derive the desired relationship between the size of an optimal set cover `C^star` and the size the cover `C` returned by the algorithm...

Proof of Approximation Result for Set Cover cont'd

Let `S_i` denote the `i` set selected by GREEDY-SET-COVER. We spread the cost of selecting `S_i`, 1, evenly among the elements covered for the first time by `S_i`. Let `c_x` denote the cost allocated to element `x in X`. If `x` is covered by `S_i`, then
`c_x = 1/(|S_i - (S_1 cup S_2 cup ... cup S_(i-1))|)`.
At each step of the algorithm, 1 unit of cost is assigned, and so
`|C| = sum_(x in X)c_x`.
The cost of the optimal cover is `sum_(S in C^star)sum_(x in S)c_x`,
and as each `x in X` is in at least one `S in C^star`, we have
`sum_(S in C^star)sum_(x in S)c_x ge sum_(x in X)c_x = |C|` (**).

We will show the theorem follows from the following claim:

Claim.`sum_(x in X)c_x le H(|S|)` for all `S in F`.

(Proof of Theorem from Claim). From (**) and the claim, we have
`|C| le sum_(S in C^star) H(|S|)`
`le |C^star| cdot H(max{|S| : S in F})`

Proof of Element Cover Cost Claim

Consider any `S in F` and `i = 1, ..., |C|`. Let
`u_i = |S - (S_1 cup S_2 cup ... cup S_(i))|`.
We define `u_0 = |S|`. Let `k` be the least index such that `u_k = 0`. At `k`, each element in S will be covered by at least one of `S_1, ... S_k`. We have `u_(i-1) ge u_i`, and that `u_(i-1) - u_i` elements of `S` are covered for the first time by `S_i`. Thus,
`sum_(x in S)c_x = sum_(i = 1)^k(u_(i-1) - u_i) cdot 1/(|S - (S_1 cup S_2 cup ... cup S_(i -1))|)`
Observe that
`|S_i - (S_1 cup S_2 cup ... cup S_(i - 1))| ge |S - (S_1 cup S_2 cup ... cup S_(i - 1))| = u_(i - 1)`
because we chose `S_i` greedily. This gives
`sum_(x in S)c_x le sum_(i = 1)^k(u_(i-1) - u_i) cdot 1/(u_(i-1))`
`= sum_(i=1)^k sum_(j = u_i + 1)^(u_(i-1))1/(u_(i-1))`
`le sum_(i=1)^k sum_(j = u_i + 1)^(u_(i-1)) 1/j` (because of the start condition of sum, `j le u_(i-1)`)
`= sum_(i=1)^k ( sum_(j = 1)^(u_(i-1)) 1/j - sum_(j = 1)^(u_(i)) 1/j)`
`= sum_(i=1)^k (H(u_(i-1)) - H(u_i))`
`= H(u_0) - H(u_k)` (telescoping series)
`= H(u_0) - H(0)`
`= H(u_0)`
`=H(|S|)`, proving the claim.

Randomized Algorithm for 2-SAT

• In a moment we will look at randomized approximation algorithms, starting with one for SAT
• Before we do, I thought I'd present a cool related algorithms for 2-SAT that uses random walks to find a satisfying assignment with high probability for instances of SAT where each clause has two literals...

Random Walks for SAT

• Consider the following algorithm for satisfiability:
  1. Start with any truth assignment `T`, and repeat the following `r` times:
     1. If there is no unsatisfied clause output "Satisfiable", halt.
     2. Otherwise, take any unsatisfied clause; pick any of its literals at random and flip its value
  2. After `r` repetitions reply "the formula is probably unsatisfiable"
• Is there a good value of `r` to choose so that this algorithm works?

Random Walks for 2SAT

Theorem. Suppose that the random walk algorithm with `r=2n^2` is applied to any satisfiable instance of 2SAT with `n` variables. Then the probability that a satisfying truth assignment will be discovered is at least `1/2`.

Proof. Let `T` be a truth assignment which satisfies the given 2SAT instance `I`. Let `t(i)` denote the number of expected repetitions of the flip step until a satisfying assignment is found starting from an assignment `T'` which differs in at most `i` positions from `T`. Notice:

1. `t(0) = 0`
2. If we find some other satisfying assignment, we do not need to continue.
3. Otherwise, we flip at least once, and we have a 50% chance of moving closer to the solution; 50% farther. So `t(i) le 1/2(t(i-1) + t(i+1)) + 1`
4. We also have `t(n) le t(n-1) + 1` (If every literal is wrong, we can only move closer).

The worst case is the when relation `t` of (3) holds as an equation. `x(0)=0`; `x(n)=x(n-1)+1`; `x(i) = 1/2(x(i-1)+x(i+1))+1`

Proof Cont'd

• As you can see above, adding all the `x(i)`'s together gives: `x(1) = 2n-1`.
• Then solving the `x(1)` equation for `x(2)` gives `4n-4`, and in general, `x(i) =2 i n-i^2`.
• Thus we have shown `t(i) le x(i) le x(n)=n^2`. Now consider the following lemma:
  Lemma (Markov Inequality). If `x` is a random variable taking nonnegative integer values, then for any `k > 0`, `Pr[x ge k cdot E(x)] le 1/k`.
  Proof. Let `p_i` be the probability that `x=i`.
  `E(x) = sum_i i cdot p_i = sum_(i le k cdot E(x)) i cdot p_i + sum_(i > k cdot E(x)) i cdot p_i > k cdot E(x) cdot Pr[x>k cdot E(x)]` Q.E.D.
• The theorem then follows taking `k=2`.