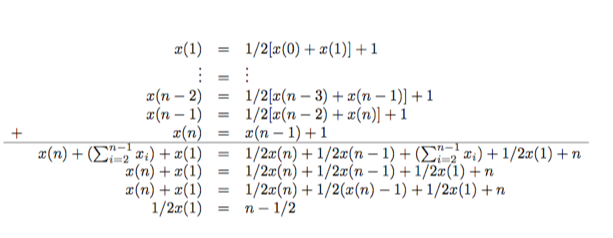Outline

• Probabilistic TMs
• BPP
• `k` Selection
• Quiz
• Random Walks

Randomized Algorithms

• We now begin to investigate the power of the Turing Machines which have the ability to flip coins.
• We begin with a very brief review of probability theorem.
• Then we define a notion of probabilistic TM and define some probabilistic complexity classes.
• After which, we consider some randomized algorithms for some common computational problems.

Probability Review -- Distributions

• A sample space `S` will for us be some collection on elementary events. For instance, results of coin flips.
• An event `E` is any subset of `S`.
• For example, if `S={HH, TH, HT, T\T}`, an event might be `{TH, HT}`
• A probability distribution `Pr_S[]` on `S` (sometimes we will also write `Pr_{s in S}[]`) is a mapping from events on `S` to the real numbers satisfying for any events `A` and `B`:
  1. `Pr_S[A] ge 0`
  2. `Pr_S[S] = 1`
  3. `Pr_S[A cup B] = Pr_S[A] + Pr_S[B]` if `A cap B= emptyset`
• Notice `1 = Pr_S[S cup emptyset] = Pr_S[S] + Pr_S[emptyset] = 1 + Pr_S[emptyset]`. So `Pr_S[emptyset] = 0`.
• Let `bar(A)` denote the complement of `A` in `S` -- all the elements of `S` that are not in `A`.
• Notice `1 = Pr_S[S]= Pr_S[bar(A) cup A] = Pr_S[bar(A)] + Pr_S[A]`. So `Pr_S[bar(A)] = 1 - Pr_S[A]`.
• Notice if we have two sample spaces, say two coin flips, `S_1`, `S_2`, each with their own distributions, `Pr_{S_1}`, `Pr_{S_2}`, we can make a product space and distribution as: `S_1 \times S_2 := {(s_1, s_2)| s_1 in S_1 \mbox{ and } s_2 in S_2 }` and `Pr_{S_1 \times S_2}[A] := \sum_{(s_1, s_2) in A} Pr_{S_1}(s_1) \cdot Pr_{S_2}(s_2)`.

Probability Review -- Random Variables

• A random variable `X` is a map `X:S -> RR`.
• Given such a function `X` we can define the probability density function for `X` as:
  `f(x) = Pr[X = x]` where the little `x in RR`.
• The expected value of a random variable `X` is defined to be: `E[X] = sum_x x cdot Pr[X=x]`

Probability Review -- Simulating a fair coin

• Let `S = {H,T}`, `Pr_S[H] = rho`, `Pr_S[T] = 1-rho`.
• Suppose we have a black box function Coin() which when we run it outputs either `H` or `T`. If we run it `n` times.
• `sum_{i=1}^n (mbox{Coin()} == H)` denotes the number of times it outputs `H`.
• We say Coin() outputs values according to `Pr_S` if `lim_{n->infty} (sum_{i=1}^n (mbox{Coin()} == H))/n = rho`.
• If `rho = 1/2` we say Coin() is fair; otherwise, Coin() is biased.
• Notice `Pr_{S\times S}[HT] = Pr_{S\times S}[TH] = rho(1-rho)`. (In the future, if the sample space is clear, we will drop it from the subscript after `Pr`).
• This suggests the following algorithm to simulate a fair black box coin function using a biased one:

  function NewCoin()
  {
     while (true) {
         x = Coin();
         y = Coin();
         if (x != y) {
             if (x == 'H') {
                 return 'H';
             } else {
                 return 'T';
             }
         }
     }
  }  
  

Probabilistic Turing Machines

Definition. A probabilistic Turing machine (PTM) is a TM with two transition functions `delta_0`, `delta_1`. To execute a PTM `M` on input `x`, we choose in each step whether to apply `delta_0` or to apply `delta_1`. These two choices give us a sample space and in what follows we always assume the probability distribution on these events gives them each probability 1/2.

The machine only outputs `1` (Accept) or `0` (Reject). We denote by `M(x)` the random variable corresponding to the value `M` writes at the end of the process. For a function `T: NN -> NN`, we say that `M` runs in time `T(n)` if for any input `x`, `M` halts on `x` within `T(|x|)` steps regardless of the choices `M` makes.

BPTIME and BPP

• So after `t` steps, a PTM might be on any one `2^t` computation branches.
• The probability that it is on a particular branch is `1/2^t`. (Here we are using the product distribution on the individual choices)
• To make a reasonable complexity class out of this model we would like that when a string is in some randomized language, then we will accept on "lot" or branches.
• Depending on how we make "lot" precise, we will end up with different complexity classes.
• For example:
  Definition (BPTIME and BPP). For `T:NN -> NN` and `L subseteq {0, 1}^star` we say that a PTM `M` decides `L` in time `T(n)` if for every `x in {0,1}^star`, `M` halts in `T(|x|)` steps regardless of its random choices and `Pr[M(x) = L(x)] ge 2/3`.
  We let `BPTIME(T(n))` be the class of languages decided by PTMs in `O(T(n))` time and define `BPP = cup_c BPTIME(n^c)`.

BPP, an alternative definition

• Recall we defined `NP` first with a verifier, later using NDTMs.
• You might ask if there is a "verifier" way to define `BPP` (or not -- but I'm going to tell you anyway).
• In fact, there is:
  Definition. A language `L` is in `BPP` if there exists a p-time TM `M` and a polynomial `p:NN->NN` such that for every `x in {0,1}^star`:
  `Pr_(r in_R {0,1}^(p(|x|)))[M(x,r) = L(x)] ge 2/3.`

Derandomization

• This equivalent formulation makes it clear that `BPP subseteq EXP` as in time `2^(poly(n))` we can cycle and count all the possible random strings and what `M`'s output on them is.
• In general, we have the following result:
  Theorem. If a BPP algorithm `A` run in time `n^k` and uses `m` bits of randomness, then there is a deterministic version of `A` that takes `2^m\cdot n^k` time.
• It is still open if `BPP = NEXP`. It is believed because of progress that has been made on derandomization that `BPP = P`, but people really don't know.
• On most programming languages, there is a "random number generator", which we use whenever we want to "fake" randomness in algorithms.
• You can think of this generator as taking a seed of `j` bits, which hopefully is random, and using it generate a sequence of `m` bits which "act random" as far as an algorithm is concerned. This is sometimes called canonical derandomization.
• We say such an algorithm is fooled if we can use just `j` bit seeds and the generator instead of the `m` bit random numbers and get the same acceptance bounds. So we have:
  Theorem. If a BPP algorithm `A` run in time `n^k` and is fooled by a pseudorandom number generator of seed length `j`, then there is a deterministic version of `A` that runs in `2^j\cdot n^k` time.
• Cryptographers typically believe certain cryptographics primitives are secure. One of these is the existence of one-way, p-time functions which are hard to invert by an randomized p-time adversary. The existence of one-way functions imply both `P != NP`, and the existence of pseudorandom number generators such that the result above implies `BPP subseteq TIME(2^{n^{epsilon}})` for all `epsilon > 0`.

Quiz

Which of the following statements is true?

1. There is an `n`-ary boolean function which requires circuits of size `2^n/{2n}`.
2. It is possible that `NP=`P/poly.
3. All languages in L/poly are recursive.

Some examples of PTMs

• A median of a set on numbers `{a_1, ..., a_n}` is any number `x` such that at least `\lfloor n/2 rfloor` of the `a_i`'s are smaller or equal to `x` and at least `\lfloor n/2 rfloor` of them are larger or equal to `x`.
• One way to find the median is to sort them and then output the `lfloor n/2 rfloor`th smallest from this list.
• This takes `O(n log n)` time.
• Here is a randomized algorithm for this problem (actually finding the `k`th smallest element) that run is expected `O(n)`.
  Algorithm FindKthSmallest(`k, a_1, ..., a_n`)
  1. Pick a random `i in [n]` and let `x=a_i`.
  2. Scan the list `{a_1, .., a_n}` and count the number `m` of `a_i`'s such that `a_i le x`.
  3. If `m=k` then output `x`.
  4. Otherwise, if `m > k`, then copy to a new list `L` all elements such that `a_i le x` and run FindKthElement(k, L)
  5. Otherwise, if `m < k` copy to a new list `H` all elements such that `a_i > x` and run FindKthElement(`k-m, H`).

Runtime of FindKthElement

Claim. For every input `k, a_1, ..., a_n` to FindKthElement, let `T(k, a_1, ..., a_n)` be the expected number of steps the algorithm takes on this input. Let `T(n)` be the maximum of `T(k, a_1, ..., a_n)` over all length `n` inputs. Then `T(n) = O(n)`.

Proof. We can prove by induction that `T(n) < 10cn`. Fix some inputs `k, a_1, ..., a_n`. For every `j in [n]` we choose `x` to be the `j`th smallest of `a_1, ..., a_n` with probability `1/n`, and then we perform either at most `T(j)` steps or `T(n-j)` steps. Thus, we have:
`T(k, a_1, ..., a_n) le cn + 1/n(sum_(j>k)T(j) + sum_(j < k)T(n-j))`
Plugging in our induction hypothesis that `T(j) le 10cj` for `j < n`, gives
`T(k, a_1, ..., a_n) le cn + 10 frac(c)(n)(sum_(j>k) j + sum_(j < k)(n-j)) le cn +10 frac(c)(n)(sum_(j > k) j +kn - sum_(j < k) j)`
Next using `sum_(j > k) j le (n(n-k))/2` and `sum_(j < k)j ge frac(k^2)(2)(1 - o(1)) ge k^2/2.5`, we get
`T(k, a_1, ..., a_n) le cn + 10 frac(c)(n)((n(n-k))/2 +kn - k^2/2.5) = cn + 10 frac(c)(n)(n^2/2 + (kn)/2 - k^2/2.5)`
Considering separately the cases `k < n/2` and `k> n/2` we can see this last equation is always less than `cn + (10c)/n (9n^2)/10 = 10cn`.

Remark. The decision problem corresponding to the above is given `z, k, a_1, ..., a_n`, is `z` the `k`th smallest element of `a_1, ..., a_n`? The algorithm above always outputs the correct answer, but uses randomness, and its expected running time is `O(n)`. Since you can also show its worst run-time is `O(n^2)` it is a BPP algorithm.

Random Walks for SAT (Pap91)

• Consider the following algorithm for satisfiability:
  1. Start with any truth assignment `T`, and repeat the following `r` times:
     1. If there is no unsatisfied clause output "Satisfiable", halt.
     2. Otherwise, take any unsatisfied clause; pick any of its literals at random and flip its value
  2. After `r` repetitions reply "the formula is probably unsatisfiable"
• Is there a good value of `r` to choose so that this algorithm works?

Random Walks for 2SAT

Theorem. Suppose that the random walk algorithm with `r=2n^2` is applied to any satisfiable instance of 2SAT with `n` variables. Then the probability that a satisfying truth assignment will be discovered is at least `1/2`.

Proof. Let `T` be a truth assignment which satisfies the given 2SAT instance `I`. Let `t(i)` denote the number of expected repetitions of the flip step until a satisfying assignment is found starting from an assignment `T'` which differs in at most `i` positions from `T`. Notice:

1. `t(0) = 0`
2. If we find some other satisfying assignment, we do not need to continue.
3. Otherwise, we flip at least once, and we have a 50% chance of moving closer to the solution; 50% farther. So `t(i) le 1/2(t(i-1) + t(i+1)) + 1`
4. We also have `t(n) le t(n-1) + 1` (If every literal is wrong, we can only move closer).

The worst case is the when relation `t` of (3) holds as an equation. `x(0)=0`; `x(n)=x(n-1)+1`; `x(i) = 1/2(x(i-1)+x(i+1))+1`

Proof Cont'd

• As you can see above, adding all the `x(i)`'s together gives: `x(1) = 2n-1`.
• Then solving the `x(1)` equation for `x(2)` gives `4n-4`, and in general, `x(i) =2 i n-i^2`.
• Thus we have shown `t(i) le x(i) le x(n)=n^2`. Now consider the following lemma:
  Lemma (Markov Inequality). If `x` is a random variable taking nonnegative integer values, then for any `k > 0`, `Pr[x ge k cdot E(x)] le 1/k`.
  Proof. Let `p_i` be the probability that `x=i`.
  `E(x) = sum_i i cdot p_i = sum_(i le k cdot E(x)) i cdot p_i + sum_(i > k cdot E(x)) i cdot p_i > k cdot E(x) cdot Pr[x>k cdot E(x)]` Q.E.D.
• The theorem then follows taking `k=2`.

WalkSAT

• Our 2-SAT algorithm is a randomized, quadratic algorithm for 2-SAT. The best deterministic algorithms are `O(n)`.
• It can be made into an algorithm for 3-SAT, which is both simple and competitive with the best deterministic algorithm (better often in practice).
• We modify the procedure of the previous slide, by choosing `r` to be `3n` and rather that halt if after `3n` steps we don't find an assignment, we choose a new `T` uniformly at random. This step is called a random restart. We do this up to `(4/3)^n` times before outputting unsatisfiable.
• Schoning proved by an analysis like the one we carried out that `(4/3)^n` trials suffices to find a satisfying assignment with high probability.