Outline

• Schaeffer's Dichotomy Theorem
• Thresholds for Satisfiability
• In-Class Exercise
• DPLL algorithm
• CDCL

Introduction

• Last lecture we began looking at algorithms for determining if a set of clauses has a satisfying assignment.
• We have previously shown that any 0-1 boolean function `R(y_1, ..., y_m)`, (we call this a relation), can be computed by a set of clauses. I.e., by a CNF formula.
• A substitution instance of `R` is where we substitute different variables in `x_{i_1}, ..., x_{i_m}` for `y_1, ..., y_m` (we also allow substituting 0 and 1 into coordinates).
• Suppose we restrict our SAT instances to be of the form `^^_{j=1}^m R_{i_j}` for substitution instances relations `R_{i_j}` coming from a set of relations `S={R_1, R_2,...}`. We denote this restriction on `SAT`, `SAT(S)`.
• We identified six situations where `SAT(S)` has a polynomial time algorithm:
  1. The all 1 assignment satisfies each relation in `S`.
  2. The all 0 assignment satisfies each relation in `S`.
  3. Each relation in `S` has at most two variables.
  4. Each relation in `S` is Horn.
  5. Each relation in `S` is dual Horn.
  6. Each relation in `S` is an a linear equation mod 2.

Schaeffer's Dichotomy Theorem (1978)

Theorem. `S` is either one of the six cases we've considered and SAT(S) is in P, or SAT(S) is NP-complete.

Proof Idea. We've already established last day, if `S` is one of the six cases then SAT(S) does have a p-time algorithm. Suppose `S` does not correspond to one of the six cases. We can prove (but don't in my slides) the following lemmas:

1. If `S` contains a non-Horn relation, then one of `x != y` or `x vv y` is expressible.
2. If `S` contains a non dual-Horn relation, then one of `x != y` or `bar{x} vv \bar{y}` is expressible.
3. If `S` contains a non dual-Horn relation and a non-Horn relation then it can express of `x != y`.
4. If `S` contains a nonaffine relation and can express `x != y` then it can express all 2-ary relations that are 0 for only one value.
5. If `S` contains a non 1-assignment relation, a non 0-assignment relation, a non 2-ary relation, and can express `x != y`, `x vv y`, then it can express `R(x,y,z)` which is 1 iff exactly one of `x`, `y`, `z` is set to 1.
6. If `S` can express `R(x,y,z)` from the last step then it can express any logical relation (so in particular the 8 possible SAT clause types.)

Threshold for 3-SAT Satisfibility

• In trying to test algorithms for 3-SAT, one needs to be able to generate a large number of 3-SAT instances.
• One process for doing this for 3-SAT instances on `n` variables with `m` clauses is:

  Let C[] be an array of m clauses each element initially
  containing no variables
  Let x[i] indicate the ith variable and ~x[i] the negation of it
  for (i = 1; i <= m; i++) {
      for (j = 1; j <= 3; i++) {
          Pick at random k in {1, 2, ... n}
          Pick at random v in  {+1, -1}.
          if (v == 1) {
              C[i][j] = x[k];
          } else {
              C[i][j] = ~x[k];
          }
      }
  }
  

• Suppose one plotted a graph of the odds the set of clauses C is satisfiable as a function of `m/n`. It would look like:
  
• The shape of the graph should make sense: If we have a lot of variables and not many clauses to put constraints on their values then it should be likely we would be able to find some assignment which makes the instance true.
• Similarly, if we have a lot of clauses then we have a lot of constraints on the assignments which can make the formula true, and so its unlikely we will find a satisfying assignment.
• We can actually prove that the graph should have this shape.

Almost Surely Unsatisfiable

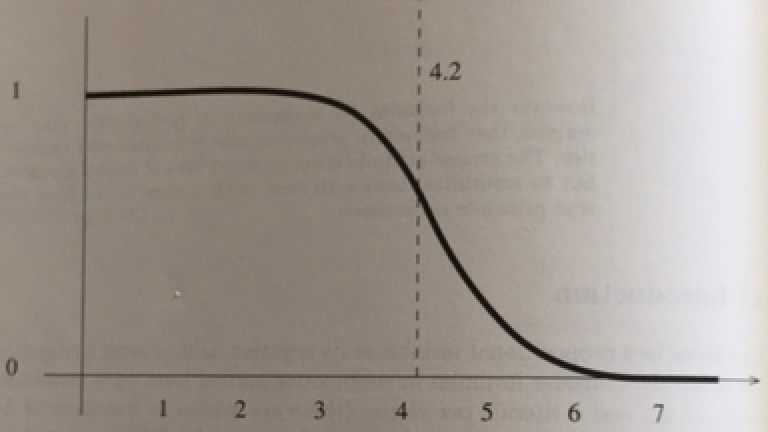
Theorem (CS88) Suppose instances of 3-SAT are chosen according to the process of the previous slide. Then if the clause to variable ratio exceeds 5.19 then as `n` the number of variables in the instances gets larger, the odds the instance is satisfiable goes to 0.

Proof. A given clause chosen by the process of the last slide will have at most a 7/8 chance of being satisfied by any given assignment. As we chose clauses independently of each other the odds an `m` clause formula will be satisfied by a particular assignment is `(7/8)^m`. The odds that some assignment on `n` variable would make an `m` clause formula 1 is less than `2^n(7/8)^m`. This will converge to 0 as `n -> infty` if `(2^n(7/8)^m)^{1/n} < 1`. We note
`(2^n(7/8)^m)^{1/n} = 2 cdot (7/8)^{m/n}`
and solving the equation `2 cdot (7/8)^{m/n} = 1` implies a value `m/n` of `- (ln2)/ln (7/8) approx 5.19`.

Almost Surely Satisfiable

• Consider the following algorithm for compute a variable assignment for 3-SAT:

  Input F a CNF formula
  Let F[0] = F
  for (t = 1; t <= n ; t++) {
      if (clauses of size 1 exist in F[t-1]) {
          L = Pick an unset literal from a uniformly randomly chosen
             clause in F[t-1] of size 1.
      } else if (clauses of size 2 exist in F[t-1]) {
          L = Pick an set literal from a uniformly randomly chosen
             clause in F[t-1] of size 2.
      } else {
          L = Pick a unset literal uniformly at random from F[t-1]. 
      }
      Set L = 1;
      F[t] = F[t-1] with the value for L substituted in;    
  }
  

• Let F be an instance of 3-SAT. (CR92) Show that if the clause to variable ratio in F is less than 3.003 then almost surely the above algorithm will find a satisfying assignment for F.

In-class Exercise

Generate a random 3SAT formula using our procedure above with 3 variables and 6 clauses. We would expect such a formula to be satisfiable.

Now apply the procedure of the previous slide to choose an assignment for the three variables. Did it satisfy your formula?

Take pictures of your work and post them to the Mar 8 Class Thread.