Outline

• Random 2SAT
• Error Reduction
• `RTime(T(n))`
• `BPP subseteq P``/poly` (Adleman)

Random Walks for SAT

• Consider the following algorithm for satisfiability:
  1. Start with any truth assignment `T`, and repeat the following `r` times:
     1. If there is no unsatisfied clause output "Satisfiable", halt.
     2. Otherwise, take any unsatisfied clause; pick any of its literals at random and flip its value
  2. After `r` repetitions reply "the formula is probably unsatisfiable"
• Is there a good value of `r` to choose so that this algorithm works?

Random Walks for 2SAT

Theorem. Suppose that the random walk algorithm with `r=2n^2` is applied to any satisfiable instance of 2SAT with `n` variables. Then the probability that a satisfying truth assignment will be discovered is at least `1/2`.

Proof. Let `T` be a truth assignment which satisfies the given 2SAT instance `I`. Let `t(i)` denote the number of expected repetitions of the flip step until a satisfying assignment is found starting from an assignment `T'` which differs in at most `i` positions from `T`. Notice:

1. `t(0) = 0`
2. If we find some other satisfying assignment, we do not need to continue.
3. Otherwise, we flip at least once, and we have a 50% chance of moving closer to the solution; 50% farther. So `t(i) le 1/2(t(i-1) + t(i+1)) + 1`
4. We also have `t(n) le t(n-1) + 1` (If every literal is wrong, we can only move closer).

The worst case is the when relation `t` of (3) holds as an equation. `x(0)=0`; `x(n)=x(n-1)+1`; `x(i) = 1/2(x(i-1)+x(i+1))+1`

Proof Cont'd

• As you can see above, adding all the `x(i)`'s together gives: `x(1) = 2n-1`.
• Then solving the `x(1)` equation for `x(2)` gives `4n-4`, and in general, `x(i) =2 i n-i^2`.
• Thus we have shown `t(i) le x(i) le x(n)=n^2`. Now consider the following lemma:
  Lemma (Markov Inequality). If `x` is a random variable taking nonnegative integer values, then for any `k > 0`, `Pr[x ge k cdot E(x)] le 1/k`.
  Proof. Let `p_i` be the probability that `x=i`.
  `E(x) = sum_i i cdot p_i = sum_(i le k cdot E(x)) i cdot p_i + sum_(i > k cdot E(x)) i cdot p_i > k cdot E(x) cdot Pr[x>k cdot E(x)]` Q.E.D.
• The theorem then follows taking `k=2`.

RTIME and RP

• Notice in the last algorithm, if we output "Satisifiable" we were always right, but if we output unsatisfiable we were sometimes wrong.
• We would like a complexity class that captures this notion of randomized algorithm as it doesn't fit exactly in the BPP framework.

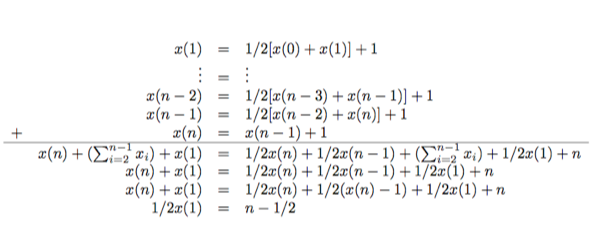
Definition. `RTIME(T(n))` contains every language `L` for which there is a probabilistic TM `M` running in `T(n)` time such that:
`x in L => Pr[M(x) = 1] ge 2/3`
`x !in L => Pr[M(x) = 1] = 0`
We define `RP = cup_c RTIME(n^c)`.

So our 2SAT algorithm was a coRP algorithm. Sometimes BPP-style randomness is called Las Vegas randomness, and RP-style is called Monte-Carlo.

`ZTIME(T(n))` and relationships

RP has "one-sided error"; one might ask for randomized algorithms that have "zero-sided error":

Definition. The class `ZTIME(T(n))` contains all the languages `L` for which there is a machine `M` that run in an expected-time `O(T(n))` such that for every input `x`, whenever `M` halts on `x`, the output `M(x)` it produces is exactly `L(x)`.

We define `ZPP = cup_c ZTIME(n^c)`.

One can show:
`ZPP = RP cap coRP`
`RP subseteq BPP`
`coRP subseteq BPP`

Error Reduction -- Chernoff Bounds

• When we defined BPP and RP we use `2/3`. Why?
• Would other choices bounded away from 1/2 work? Say 3/4?
• The answer is "Yes". For example if the bound was `3/4` we can run a `2/3` algorithm repeatedly and take the majority output to reduce the error.
• The main tool to show that this works is Chernoff Bounds:
  Lemma (Chernoff). Suppose `X_1,...,X_n` are independent random variables taking the values `1` and `0` with probabilities `p` and `1-p`. Let `X = sum_(i=1)^n X_i`. Then for all `0 le c le 1`, `Pr[X ge (1+c)pn] le e^(-(c^2pn)/2)`.

Proof of Chernoff Bounds

If t is a positive real number, then
`Pr[X ge (1+c)pn]= Pr[e^(tX) ge e^(t(1+c)pn)]` (*)
By Markov's Inequality,
`Pr[e^(tX) > k cdot E(e^(tX))] le 1/k` for any real `k > 0`.
Taking `k=e^(t(1+c)pn)/[E(e^(tX))]` and using (*) gives
`Pr[X ge (1+c)pn] le [E(e^(tX))]cdot e^(-t(1+c)pn)`. (**)
Since `X= sum_(i=1)^n X_i`, we have `E(e^(tX) )=[E(e^(tX_1))]^n` which in turn equals `(1 + p(e^t-1))^n`. Substituting this into (**) gives:
`le e^(-t(1+c)pn) cdot e^(pn (e^t-1))`, since `(1+a)^n le e^(an)`. Take `t=ln(1+c)` to get `Pr[X ge (1+c)pn] le e^(pn(c-(1+c)ln(1+c)))`. Taylor expanding `ln(1+c)` as `c - c^2/2 + ...` and substituting gives the result. i/e.,
`e^(pn(c-(1+c)ln(1+c))) le e^(pn(c-(1+c)(c- c^2/2 +c^3/3 + ...))) le e^(-(c^2 pn)/2)`

Corollary. If `p=1/2 + epsilon` for some `epsilon > 0`, then the probability that `sum_(i=1)^n X_ i le n/2` is at most `e^(-epsilon^2n/4).

Proof. Take `c = epsilon/(1/2+ epsilon)`. Q.E.D.

Robustness of BPP

• Notice if we had chosen `1/2+epsilon` in the definition for some `0 < epsilon <1/4`, in our definition, then it would not have made a difference.
• Let `k = [4ln 2/(epsilon^2)]`. Run the machine that accepts `L` according to the probabilities `1/2+epsilon` a total of `2k+1` times and accept the majority of the outcomes.
• So by Chernoff bounds, the odds that the majority vote of these runs is wrong is at most `e^(-epsilon^2(2k+1)/4) le e^(-epsilon^2(2k)/4) = e^(-8ln2/4)= 2^(-2) = 1/4`.
• Thus, we will accept with the `3/4`'s probability if its in the languages and reject with `3/4` probability if its not.

`BPP subseteq P``/poly`

The next result shows to a certain degree BPP can be derandomized:

Theorem. `BPP subseteq P``/poly`.

Suppose `L in BPP`, then there exists a TM `M` that on inputs of size `n` uses `m` random bits and such that for every `x in {0,1}^n`, `Pr_r[M(x,r) ne L(x)] le 2^(-n-1)`. Say that a string `r in {0,1}^m` is bad for an input `x in{0,1}^n` if `M(x,r) ne L(x)` and otherwise call `r` good for x. For every `x`, at most `2^m/(2^(n+1))` strings are bad for `x`. Adding over all `x in {0,1}^n`, there are at most `2^n(2^m/(2^(n+1))) = 2^m/2` strings that are bad some some `x`. In particular, there exists a string `r_0 in {0,1}^m` that is good for every `x in {0,1}^n`. We can hardwire such a string `r_0` to obtain a circuit `C` (of size at most quadratic in the running time of `M`) that on input `x` outputs `M(x,r_0)`. The circuit `C` will satisfy `C(x) = L(x)` for every `x in {0,1}^n`.