Outline

• Boolean Circuits
• Quiz
• P/Poly
• Logspace Uniformity
• Karp-Lipton Theorem
• Meyer's Theorem
• Shannon's Theorem

Boolean Circuits

• Boolean circuits are a more succinct way to represent Boolean functions than Boolean formulas (aka Boolean Expressions).
• Boolean circuits allow us to reuse computations we have already done. For example:
  

Boolean Circuits Formal Definition

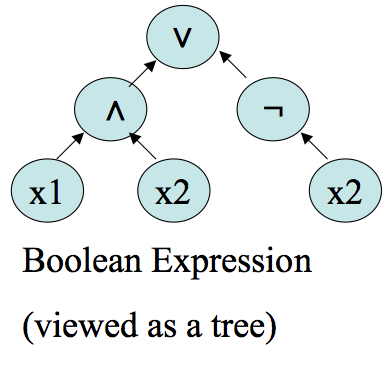
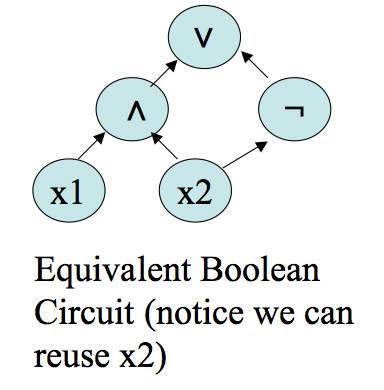
Definition. A Boolean circuit is a directed, acyclic, labeled graph `(V, E, s)`, where `s:V ->{mbox(set of labels)}`. We assume the vertices are numbered `1, ...,n`. All vertices in the graph have indegree `0`, `1`, or `2`. Those of indegree `0` are called inputs and are labeled with variables or true or false. Those of indegree 1 are must be labeled with `neg` and those of indegree 2 can be labelled with `vv` or `^^`. We require the inputs `j`, `k` to any gate `i` be such that `j < i`, `k < i`. Gate `n` is called the output and has outdegree `0`.

• To figure out the output of a circuit for a given truth assignment to the input variables we can evaluate the circuit from the lower numbered gates to the higher numbered gates using the usual rules for `vv`, `^^` , `neg` at each gate.
• This procedure can be implemented in polynomial time. Given a circuit with all of its inputs assigned a value, the problem of determining the output is called the CIRCUIT VALUE PROBLEM (CVP). So we have:
  Proposition. `CVP in P`.
• In contrast, the problem of determining whether a given circuit is satisfiable (`mbox(CIRCUIT-SAT)`) is not known to be in polynomial time.
• Given that `CVP in P` it follows that `mbox(CIRCUIT-SAT) in NP`. On the other hand, as any Boolean formula is a circuit and satisfiability for Boolean formulas is `NP`-hard, we have that `mbox(CIRCUIT-SAT)` is `NP`-hard. Hence,
  Proposition. `mbox(CIRCUIT-SAT)` is `NP`-complete.

Quiz

Which of the following is known to be true? (More than one)

1. `SAT in NP^(SAT)`.
2. `SAT in coNP^(SAT)`.
3. `NP^(SAT) subseteq Pi_3^p`.

Polynomial Size Circuits

• The size of a circuit is the number of gates in it.
• We next would like to define what it means for a family of circuits to recognize a language:
  Definition. A family of circuits is an infinite sequence `(C_0, C_1, ... )` of Boolean circuits, where `C_n` has `n` input variables. We say a language `L` has polynomial size circuits, if there is a polynomial `p` such that `SIZE(C_n) < p(n)` and `C_n` accepts exactly those strings in `L` of length `n`.
• We call the class of languages with polynomial circuits `P``/poly`.

P is in P/Poly

Theorem. All languages in P have polynomial size circuits.

Proof. Let `L in P` be decided by `M` in `n^k` time. WLOG, we can assume `M` uses only one tape. We construct circuits `C_n` such that for `x` such that `|x| = n`, `C_n(x) = 1 iff x in L`. The inputs to this circuit will be `n` variables `x_1, ..., x_n` representing the bits of `x`. We imagine we encode configurations of a TMs as binary strings representing `(`squares seen so far to left of head, state, squares seen so far to right of tape head (or input squares not seen)`)`. The circuit computes from the input string a start configuration of `M`. It then consists of `n^k`-layers, where the `i+1`st layer computes the configuration one would be in given the `i`th layer's configuration. Finally, we take the last layer and have a circuit which computes from it the output of the TM. The total size of this will be `O(n^(2k))`.

Corollary. CVP is `P`-complete under logspace reductions.

Proof. Suppose `L in P`. To reduce `x in L`? to `CVP` we compute the circuit of the last theorem, then we hard code the input bits to be `x` and ask the result to CVP. one can verify this can be computed in logspace.

Uniformity

Definition. We call a circuit family `(C_0, C_1, ... )` logspace-uniform if there is a `(log n)`-space machine `N` which on input `1^n` outputs `C_n`. We say that a language `L` has logspace-uniform polynomial circuits if there is a uniform family of p-size circuits that decides `L`.

Theorem. A language `L` has logspace-uniform polynomial circuits iff `L` is in `P`.

Proof. One direction follows from the theorem of the last slide recall completeness of CVP was logspace computable. For the other direction suppose that `L` has logspace-uniform polynomial circuits. In p-time we can decide `x in L` by first running the logspace machine to get `C_(|x|)` then doing circuit evaluation on `x` in p-time.

Advice Classes

• An advice string is a map from positive integers to strings.
• We say a machine `M` decides a language `L` with advice string `A(n)` if `x in L` implies `M(x, A(|x|))` accepts. And if `x` is not in `L` then `M(x, A(|x|))` rejects.
• Let poly denote the set of advice strings `A(n)` such that `|A(n)| < p(n)` for some polynomial `p(n)`.
• We say a language `L` is in `P``/poly` if there is a a p-time `M` that decides `L` using an advice string in poly.
  Proposition. This and our previous definition of `P``/poly` are equivalent.

  Proof. Notice given `n` the encoding of a a circuit `C_n` is polynomial size and could serve as advice to a machine that essentially computes the value of the circuit on an input. This shows the circuit version of `P``/poly` is contained in the advice version. On the other hand, we can hard-code an advice string as part of the inputs to a circuit `C_n` simulating M(x, y) on inputs on of length `n`. This shows the advice version is contained in the circuit version of this class.

Karp-Lipton

Theorem (K-L 80). If `NP subseteq P``/poly`, then `PH = Sigma_2^p`.

Proof. If suffices to show that `Pi_2^p = Sigma_2^p`. In particular, to show that `Pi_2`-SAT is contained in `Sigma_2^p`. Let
`forall u in {0,1}^n exists v in {0,1}^n phi(u,v)=1`
be an instance of `Pi_2`-SAT. Here `phi` is a Boolean formula.

If `NP subseteq P``/poly`, then there exists a circuit family `{C_n}` of size some polynomial `p` such that for every Boolean formula `phi` and `u in {0,1}^n`, `C_n(\phi, u) = 1` iff there exists a `v in {0,1}^n` such that `phi(u,v) = 1`. As stated this circuits solves the SAT decision problem for `phi`. As we showed earlier in this semester we can take such a family of `C_n`'s and modify them so that they actually output the witness `v`. Call this new family of circuits `{B_n}`. The size of `{B_n}` will also be bounded by some polynomial `q` and encoding of such a circuit as a string can be bounded by `10q(n)^2`. Our `Sigma_2^p` essentially guesses such a circuit and verifies that it works. i.e., it checks the following formula: `exists w in {0,1}^(10q^2)forall u in {0, 1}^n mbox(s.t. w describes a circuit B and ) phi(u,B(phi, u)) = 1.`

Meyer's Theorem

Theorem (K-L 80). If `EXP subseteq P``/poly` then `EXP = Sigma_2^p`.

Remark. This theorem actually served as one of the inspirations behind the recent result (2010) of Williams that `A \C \C` does not contain `NEXP`.

Proof. Let `L in EXP`. Then `L` is computable by a `2^(p(n))` time oblivious TM `M` where p is some polynomial. Let `x in {0, 1}^n` be some input string. For every `i in [2^(p(n))]` we denote by `z_i` the encoding of the `i`th snapshot of `M`'s execution on `x`. If `M` has `k` tapes, then `x in L` iff for every `k+1` indices `i`, `i_1`, ..., `i_k`, the snapshots `z_i`, `z_(i_1)`, ..., `z_(i_k)` satisfy some easily checkable criteria: If `z_i` is the last snapshot, then it should encode `M` outputting `1`, and if `i_1`, .., `i_k` are the last indices where `M`'s heads were in the same locations as in `i`, then the values in `z_i` should be consistent with the values in the `z_(i_j)`'s. If `EXP subseteq P``/poly` then there is a `q(n)`-sized circuit `C` that computes `z_i` from `i`. The correctness of this transcript can be computed by a `coNP` (one that checks that the transcript satisfies all local criteria). Hence `x in L` iff
`exists C in {0,1}^(q(n))forall i, i_1, ..., i_k in {0, 1}^{p(n)} T(x, C(i), C(i_1), ... C(i_k)) = 1`.
where `T` is some p-time TM checking these conditions. Hence `L in Sigma_2^p`.

A Counting Argument

Theorem (Shannon 1949). For any `n ge 2` there is an n-ary Boolean function `f` such that no Boolean circuit with `2^n/(2n)` or fewer gates can compute it.

Proof. We know there are `2^(2^n)` n-ary boolean functions. Let `m = 2^n/(2n)`. Let's get an upper bound on how many circuits there are with at most this many gates. For each gate in such a circuit we have at most `(n+5)` choices for the gate type and at most `m^2` choices for the gate inputs. As there are at most `m` gates in the circuit, we get at most `((n+5)m^2)^m` possible circuits of size `m`. Let's compare this with `2^(2^n)` by taking the `log` of both functions and recalling `m= 2^n/(2n)`. The `log` of the number of n-ary Boolean functions is `2^n`, on the hand the `log` of the number of circuits is `2^n [1- (log([4n^2/(n+5)]))/(2n)]`. So some function must have been missed.

Size Hierarchy

Theorem. For every functions `T`, `T': NN -> NN` with `2^n/n > T'(n) > 10T(n) > n`,
`SIZE(T(n)) stackrel(subseteq)(ne) SIZE(T'(n))`.

Proof. More general results of this proven via diagonalization can be found in Pollett 2005. To show the idea, we prove that `SIZE(n) stackrel(subseteq)(ne) SIZE(n^2)`. By the Shannon's Theorem for every `l` there is a function `f:{0,1}^l -> {0,1}` that is not computable by `2^l/(2n)` sized circuits. On the other hand, we know every Boolean function from `{0,1}^l` to `{0,1}` is computable by a `2^l 10 cdot l`-sized formula/circuit.

Therefore, if we set `l = 1.1 log n` and let `g:{0,1}^n -> {0,1}` be the function that applies `f` on the first `l` bits of the input, we get
`g in SIZE(2^l 10 cdot l) = SIZE(11n^(1.1) log n) subseteq SIZE(n^2)`
`g !in SIZE(2^l/2n) subseteq SIZE(n^(1.1)/ (11 log n)) supseteq SIZE(n)`.

Circuit classes Within `P`

• The depth of a circuit is the length of the longest directed path from an input node to the output node.
  Definition. For every `d`, a language `L in NC^d` if `L` can be decided by a family of circuits `{C_n}` where `C_n` has poly(n) size and depth `O(log^d n)`. The class `NC` is `cup_(i ge 1) NC^i`.
• NC is short for Nick (Pippenger)'s Class.
• The graph of multiplication, addition, and division of `n`-bit integers can be shown to be in `NC^1`.
• For `d > 1`, one can look at logspace-uniform `NC^d` circuit families. For `d=1`, one needs to look at more restrictive versions of uniformity.
• Uniform `NC` can be shown to capture those algorithms which can be solved with `n^(O(1))` processors in `log^(O(1)) n` time -- one notion of efficiently parallelizible algorithms.
• We can imagine allowing AND and OR gates to take more than `2` inputs. i.e., being of unbounded fan-in.
• The class `AC^d` is defined in the same way as above except allowing circuits unbounded fan-in ORs and ANDs.
• It turns out `cup_k AC^k = AC=NC = cup_k NC^k`.
• It can be shown that parity is not in `AC^0`.