Outline

• Volume Modeling
• Medial Axis Representation
• Data Structures in Boundary and Volume Representations

Introduction

• Before the Midterm we were looking at the material in Chapter 5 from Agoston.
• In particular, we had given an abstract definition of a representation scheme for a set of objects.
• Then we had considered briefly several such representations schemes such as b-reps, Euler representations, sweep reps, and decomposition schemes.
• Today, we are going to look at a few more representation schemes and then talk about data structures for representations schemes.

Volume Modeling

• When, we talked about parametric representation schemes we mentioned that one can represent things with 3D-parametrizations. i.e., parametrizing based on the volume of an object rather than its surface.
• Volume modeling deals with modeling volumes rather than surfaces of objects.
• Some terms which come up in this context are:
  • Volumetric data -- Data about each voxel that makes up a volume.
  • Volume Modeling -- The synthesis, analysis and manipulation of sampled, computed, and synthetic objects contained within a volumetric data set.
  • Volume Visualization -- A visualization method concerned with the representation, manipulation, and rendering of volumetric data.
  • Volume Graphics -- The subfield of computer graphics that employs a volume buffer for scene representation and is concerned with synthesizing, manipulating, and rendering such scenes.
• Volume modeling is often used for medical imagery as well as modeling natural phenomena such as fluid dynamics and weather.
• Some advantages of volume modeling for CAD are the ability to do cut-away views of objects, CSGs for voxels tend to be easy, rendering is viewpoint independent, it is independent of scene and object complexity.
• Some disadvantages of volume modeling are: that it requires a large amount of data to be maintained, discretization often results in a loss of information, and voxelization and cause aliasing effects.

Medial Axis Representation

• This representation is often used in conjunction with other representations.
• The idea is to create a skeleton for an object and then say how its exterior hangs on this skeleton (for instance when the object moves.)
• Skeletons come in two flavors: continuous and discrete. We will only consider the continuous case
• We next give some definitions which will help describe the continuous case.

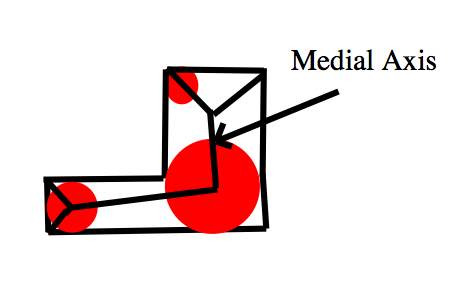
Definition. Let `X \subseteq \mathbb{R}^n`. A maximal disk in `X` is a closed disk `D^n(\vec{p}, r)` contained in `X` with the property that it is not properly contained in any other closed disk in `X`.

Definition. Let `X \subseteq \mathbb{R}^n`. The medial axis (MA) or skeleton or symmetric axis of `X` is the closure of the set of centers of maximal disks in `X`. The medial axis of a 3D solid is sometimes called a medial surface. The real-valued function that assigns to each center of a maximal disk in `X` the radius of that disk extends to a continuous function on the medial axis called the radius function.

Example of MA and Maximal Disks

More on Medial Axis

• The medial axis for a polyhedron has a natural partition into cells. Determining the rep reduces to determining this cell decomposition.
• In 2D, the cells are called arcs (the curves) and junctions (where two or more curves meet).
• In 3D, you get sheets, seams, and junctions. (Try to visualize what the medial axis for a flat box would be.
• The medial axis representation or medial axis transform of an object consists of its medial axis together with the associated radius function.
• We will look at techniques for finding the medial axis representation based on Voronoi Diagrams and Delauney Triangulation later in the semester.

Data Structures for Boundary Representations

• A common problem in geometric modeling is to choose data structures for the geometry that is to be modeled.
• We want our structures to be such that they are both efficient in both memory needed as well as time needed for rendering.
• We next look at some data structures for b-reps of linear polyhedra.
• Rendering such polyhedra involves two parts: the structure of the complex, and the actual data points. To describe the structure means describing the various adjacency relations between cells of the space.

Definition. A `d`-dimensional cell is said to be adjacent to an `e`-dimensional cell if:

1. `d \ne e` and one is contained in the other.
2. `d = e > 0`, and they have a (`d-1`)-dimensional cell in common, or
3. `d = e = 0`, and they are the two ends of some 1-dimensional cell.

Adjacency Relations

• To keep things simple we will temporarily talk about two dimensional complexes. So we will be interested in vertices V, edges E, and faces F.
• Given two cell we write `x rightarrow y` to say `x` is adjacent to `y`. We write `x rightarrow Y` to denote the set of objects of type Y (i.e., V, E, or F) adjacent to `x`. Finally, we write `X rightarrow Y` to denote the set of objects of type X adjacent to an object of type Y.
• If a data structure contains one of these adjacency relations explicitly, then we say that it has direct access to that information.
• So `E rightarrow V` denotes the set of edges that have direct access to both of its vertices.
• We write `|X|` to denote the number of object of type `X`.
• Two natural questions about data structures are: Does the data structure adequately describe the topology of the spaces that are represented? What is the complexity of determining the truth of `x rightarrow y`? or `x rightarrow Y` given the information in the data structure?

Baumgart's Winged Edge Representation

• In this representation each face is assume to be bounded by a set of disjoint edge cycles. One of these is the outside boundary, and the others are the holes in the faces.
• To implement this, one uses a face table that consists of the edges where one takes one edge from each face cycle.
• Each vertex has to a circularly ordered set of edges that use it.
• Each edge has:
  • The incident vertices
  • The left face and right face
  • The preceding and succeeding edge in clockwise order with respect to the exterior of the solid
  • The preceding and succeeding edge in counter-clockwise order with respect to the exterior of the solid.
• This representation gives us direct access to `E\rightarrow V`, `V\rightarrow E`, `E\rightarrow E`, `E\rightarrow F` and `F\rightarrow E`.

Winged Edge Representation Data Structures from

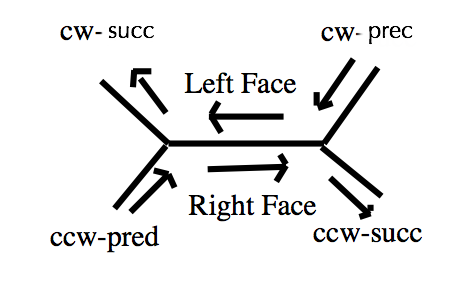
Here are some example data structures for Winged edge representation from Wikipedia:

class WE_Edge {
  WE_Vertex vert1, vert2;
  WE_Face aFace, bFace;
  WE_Edge aPrev, aNext, bPrev, bNext; // clockwise ordering
  WE_EdgeDataObject data;
}
class WE_Vertex {
  List<WE_Edge> edges;
  WE_VertexDataObject data;
}
class WE_Face {
  List<WE_Edge> edges;
  WE_FaceDataObject data;
}

Data Structures for Volume Modeling

• One way to represent volumes is to use a tree structure to cut down on the data one has to store.
• The basic algorithm for representing a volume as a tree looks something like:
  • If the volume is empty or completely covered by the object, then no further subdivision is done and the volume is marked EMPTY or FULL respectively.
  • Otherwise, subdivide the volume and recursively repeat these two steps on each of the subvolumes.
• Notice in the above we have not specified how to subdivide the given volume. If one just splits the volume in two with a line in 2D or a plane in 3D, into two sides with roughly the same volume one is on the road to getting a BSP-tree (binary space partitioning) tree.
• The algorithms to do this partitioning can be hard. An easier solution for 2D is to assume the figure is in some square and then one partitions, one partition the square into its natural four sub-squares.
• The resulting tree is called a quadtree. The 3D analog with cubes gives rise to octrees.